Одним из разделов в ЕГЭ по информатике является «Моделирование и компьютерный эксперимент». Основное понятие в данном разделе – это модель. Модель - это объект, который создается искусственно и дает упрощенное представление о реальном объекте, процессе или явлении, отражающий существенные стороны изучаемого объекта с точки зрения цели моделирования. Следовательно, моделирование - это создание моделей, которые предназначены для изучения и исследования объектов, процессов или явлений.[2]
Данный раздел в школьной программе по учебно-методическому комплексу автора Л.Л. Босовой начинают изучать с 6 класса. Учащихся знакомят с понятиями информационного моделирования, а так же с его разнообразием. В учебниках представлены знаковые (словесные, математические модели), табличные информационные модели, графики, диаграммы, схемы. С каждым классом объем знаний по разделу добавляется и усложняется, например, в 6 классе изучаются информационные модели в виде таблиц «объект – свойства», «объект – объект», то есть рассматриваются типы связи «один к одному» и «один ко многим». В 7 классе в раздел моделирование добавляются информационные модели, описывающие связи «многие ко многим», например «объекты – объекты», «объекты – свойства – объекты». Для подготовки учеников к ГИА и ЕГЭ, начиная с 8 класса, после каждой главы учебника расположены тестовые задания для самоконтроля.
При решении задач по информатике в области моделировании школьникам приходится сталкиваться с различными видами информационных моделей. В данной статье рассмотрим задачу по моделированию, которая связана с анализом графиков и диаграмм в электронных таблицах, а также разберем особенности решения задачи построения кратчайшего пути в таблице смежности для формирования навыков учащихся исследования графов.
Граф — совокупность непустого множества вершин и наборов пар вершин (связей между вершинами)[1]. Объекты представляются как вершины, или узлы графа, а связи — как дуги, или рёбра[3]. Графы применяются в разных областях, для каждой области применяется определенные, которые имеют свою направленность, ограничения, а так же дополнительные данные о вершинах и ребрах.
Графы можно представить различными способами:
1) графический способ – изображение графа;
2) список ребер – перечисление всех ребер графа как пар обозначений связываемых этими ребрами вершин;
3) матрица смежности – квадратная симметричная таблица, в которой столбцы и строки соответствуют вершинам графа, а на пересечении ячеек записываются числа, обозначающие наличие или отсутствие связей между соответствующими парами вершин;
4) матрица инцидентности – таблица, строки которой соответствуют ребрам, а столбцы – вершинам, на пересечении ячеек указывается связь между инцидентными элементами графа (ребро и вершина).
Таблица – это систематизированный перечень цифровых данных или каких-либо иных сведений, расположенных в определенном порядке по графам.
Диаграмма – это графическое представление данных. Они используются для анализа и сравнения данных, представления их в наглядном виде.
Существуют различные виды диаграмм:
1) гистограмма – графическое представление в виде прямоугольников одинаковой ширины, расположенных вертикально, одиночные прямоугольники либо сгруппированные по определенному признаку. применяются для распределения числовых значений какого-либо показателя во времени или по составным частям;
2) линейчатые диаграммы – графическое представление в виде прямоугольников, расположенных горизонтально. высота прямоугольников соответствует числовым значениям сравниваемых величин;
3) круговая диаграмма – графическое представление в виде окружности, круга. применяется для изображения удельного веса составных частей какого-либо целого (в долях или процентах).
Рассмотрим типовые задачи по моделированию.
Пример 1.
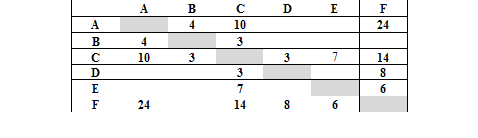
Между городами A, B, C, D, E, F проложены дороги, протяженность которых приведена в таблице (отсутствие числа в таблице означает, что дороги нет). Определите длину кратчайшего пути между городами А и F (при условии, что передвигаться можно только по построенным дорогам).
Решение:
Нам дана таблица смежности, следовательно, эта задача на построение графа. Вершинами графа являются названия городов, от A до F, а ребра определяются наличием в таблице чисел, указывающих вес этих ребер. Расставляем вершины и соединяем линиями, только те на пересечении столбца и строки имеются непустые ячейки. Число, в соответствующих ячейках, записываем над ребрами.
В условии задачи не говорится, что движение в одном направлении, следовательно, граф не является ориентированным. Матрица смежности зеркально симметрична (т.е. ячейки над главной диагональю и под симметричны).
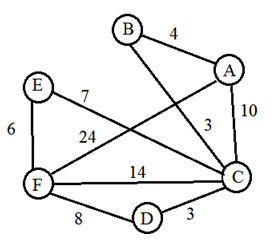
Граф для данной таблицы смежности:
Методом перебора, перечислим все возможные пути от A к F и определим самый короткий путь.
AF – длина пути: 24;
ABCDF – длина пути: 4+3+3+8=18;
ABCF – длина пути: 4+3+14=21;
ABCEF – длина пути: 4+3+7+6=20;
ACDF – длина пути: 10+3+8=21;
ACF –длина пути: 10+14=24;
ACEF –длина пути: 10+7+6+23.
Самый короткий путь – ABCDF длиной 18 единиц.
Пример 2.
Дан фрагмент электронной таблицы.
|
№ |
A |
B |
C |
D |
|
1 |
|
1 |
2 |
|
|
2 |
=C1/2 |
=(A2+B1)/2 |
=C1–B1 |
=2*B2 |
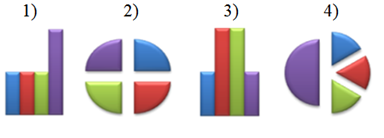
После выполнения вычислений была построена диаграмма по значениям диапазона ячеек A2:D2. Укажите получившуюся диаграмму.
Решение
Вычисляем значения формул и вписываем их в таблицу:
|
№ |
A |
B |
C |
D |
|
1 |
|
1 |
2 |
|
|
2 |
1 |
1 |
1 |
2 |
Анализируем ответ:
- 2-й вариант не подходит, т.к. все доли равны.
- 3-й не соответствует, т.к. A2 и D2 равны и меньше B2 и C2.
- 4-й является не верным, т.к. D2=A2+B2+C2, а согласно таблице: 2=1+1+1 – равенство не верное, значит ответ не правильный.
Ответ: диаграмма № 1 (поскольку A2,B2,C2 равны между собой и каждая из этих долей вдвое меньше D2).
Навыки анализа информационных моделей, умение конструировать оптимальные маршруты в графах способствуют развитию логического мышления детей. Задачи компьютерного моделирования учат школьников не только выполнять вычисления, использовать математические формулы и логику, но и дают возможность самостоятельно исследовать законы и явления из разных научных областей, сравнивать и давать анализ объектам.
Библиографический список
- Karmanova E.V., EfimovaI.Yu., Guseva E.N., Kostina N.N., Saveleva L.A., Bobrova I.I.//Modeling of students’ competency development in the higher education distant learning system. –В сборнике: Proceedings of the 2016 Conference on Information Technologies in Science, Management, Social Sphere and Medicine (ITSMSSM 2016) 2016. С. 308-315.
- Гусева Е. Н. Информатика: [электронный ресурс] учеб.пособие/ Е. Н. Гусева, И.Ю. Ефимова, Р.И. Коробков, К.В. Коробкова, И.Н. Мовчан, Л.А. Савельева. – 3-е изд., стереотип. – М.: Флинта, 2011.– 260 с.–Режим доступа: http://www.knigafund.ru/books/116085
- Гусева Е.Н. Анализ результатов имитационного моделирования в среде Rockwell Software Arena /В сборнике: Теплотехника и информатика в образовании, науке и производстве сборник докладов V Всероссийской научно-практической конференции студентов, аспирантов и молодых учёных (TИМ’2016) с международным участием. Министерство образования и науки Российской Федерации, Уральский федеральный университет имени первого Президента России Б. Н. Ельцина, Институт материаловедения и металлургии, Кафедра «Теплофизика и информатика в металлургии». 2016. С. 194-198.
- Гусева Е.Н. Дидактические условия использования педагогических программных средств в процессе профессиональной подготовки будущих учителей: дис. канд. пед. наук.– Магнитогорск, 1999, – 168 с.
- Гусева Е.Н. Задачи на измерение количества информации с использованием понятия вероятности// Информатика и образование. – М.: № 2, 2008. –С. 61-64.
- Гусева Е.Н. Имитационное моделирование как среда компьютерной визуализации знаний/ В книге: Новые информационные технологии в образовании/ Материалы VII международной научно-практической конференции. Российский государственный профессионально-педагогический университет. 2014. С. 395-399.
- Гусева Е.Н. Математические основы информатики/ Е.Н. Гусева, И.И. Боброва, И.Ю. Ефимова, И.Н. Мовчан, С.А. Повитухин, Л.А. Савельева. – Магнитогорск: Изд-во Магнитогорск. гос. техн. ун-та им. Г.И. Носова, 2016.- 234 с.
- Гусева Е.Н. Основы имитационного моделирования экономических процессов: лаб. практикум / Е.Н. Гусева. – Магнитогорск: МаГУ, 2007. – 140с.
- Ермакова Т.А., Гусева Е.Н. Использование компьютерного моделирования в преподавании геометрии // Современные научные исследования и инновации. 2016. № 6 [Электронный ресурс]. URL: http://web.snauka.ru/issues/2016/06/68886 (дата обращения: 24.06.2016).
- Информатика и информационные технологии. Тема 9. Информационное моделирование. Электронный ресурс: http://www.ido.rudn.ru/nfpk/inf/inf9.html.
- Казачков И.А., Гусева Е.Н. Компьютерная модель «Хищник-Жертва» // Современные научные исследования и инновации. 2017. № 1 [Электронный ресурс]. URL: http://web.snauka.ru/issues/2017/01/77530
- Никулина Н.М., Гусева Е.Н. Задачи компьютерного моделирования в школьном курсе информатики // Современные научные исследования и инновации. 2017. № 1 [Электронный ресурс]. URL: http://web.snauka.ru/issues/2017/01/76147
- Саралашвили А.А., Гусева Е.Н. Компьютерное моделирование демографических процессов // Современные научные исследования и инновации. 2017. № 1 [Электронный ресурс]. URL: http://web.snauka.ru/issues/2017/01/77136
- Татарникова В.В., Гусева Е.Н. Использование компьютерного моделирования в решении задач о системах массового обслуживания // Современные научные исследования и инновации. 2016. № 6 [Электронный ресурс]. URL: http://web.snauka.ru/issues/2016/06/69373 (дата обращения: 07.07.2016).
Количество просмотров публикации: Please wait