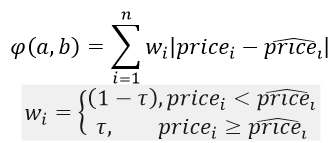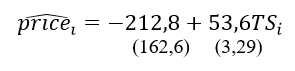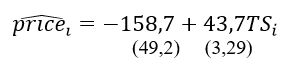Введение
Приобретение нового жилья во все времена являлось важным и затратным приобретением. На этапе выбора объекта покупки возникает масса сомнений по поводу выбора предпочтительного критерия. В первую очередь у покупателя возникает вопрос, на каком рынке лучше приобрести недвижимость? На первичном или вторичном? Как купить квартиру с максимальной выгодой, по минимальной цене? На что следует обратить внимание в первую очередь? Какие факторы влияют на формирование цены? Для ответа на все эти вопросы необходимо учесть ряд параметров таких как: количество комнат, общая площадь, площадь кухни, наличие балкона или лоджии, этаж расположения квартиры, тип дома, срок сдачи в эксплуатацию и т. д.
Вследствие того, что вопрос стоимости и доступности жилья имеет крайне важное социально-экономическое значение, рынок недвижимости является объектом многочисленных исследований. При анализе цен на жилую недвижимость широко используется экономико-математическое моделирование [1-4]. Модели, которые рассматриваются в данных работах, позволяют делать прогноз стоимости жилья [1, 2], а также анализировать факторы, влияющие на ценообразование на рынке жилой недвижимости [3, 4].
Цель данной работы – выявить основные факторы, влияющие на формирование стоимости квартир на первичном рынке жилой недвижимости города Волгограда.
1. Статистические данные и методы исследования
На основе данных интернет ресурсов «ТК-Недвижимость» (URL: http://new34.ru/) и «Новостройки Волгограда» (http://новостройки-в-волгограде.рф) была осуществлена механическая выборка данных. В ходе исследования были отобраны новостройки, сдающиеся под серый ключ в Ворошиловском, Дзержинском, Советском, Кировском, Краснооктябрьском, Красноармейском и Центральном районах города Волгограда. Объем выборки составил 429 квартир. Изучались квартиры, которые пользуются наибольшим спросом – однокомнатные, двух- и трехкомнатные. Отбор данных проводился в течение III квартала 2016 года. В выборку попали квартиры в различном ценовом диапазоне: от эконом-класса до элитных квартир. В таблице 1 приведены данные о распределении квартир по районам города, которые попали в выборку.
Таблица 1. Распределение квартир по районам города Волгограда
| Район | Количество однокомнатных квартир | Количество двухкомнатных квартир | Количество трехкомнатных квартир | Общее Количество квартир |
| Ворошиловский | 18 | 15 | 9 |
42 |
| Дзержинский | 21 | 20 | 27 |
68 |
| Кировский | 14 | 24 | 8 |
46 |
| Красноармейский | 7 | 5 | 6 |
18 |
| Краснооктябрьский | 23 | 37 | 8 |
68 |
| Советский | 70 | 46 | 31 |
147 |
| Центральный | 12 | 13 | 15 |
40 |
| По всем районам | 165 | 160 | 104 |
429 |
В качестве регрессоров, влияющих на стоимость квартиры price (в тыс. руб.), рассматривались следующие переменные:
TS – общая площадь квартиры (м2);
BS – площадь балкона (лоджии) (м2, при отсутствии балкона площадь принималась равной нулю);
time – время, в течение которого дом планируется сдать в эксплуатацию (в кварталах);
brick – фиктивная переменная, которая принимает значение 1, если дом кирпичный и значение 0, если дом не кирпичный;
R1 – фиктивная переменная, которая принимает значение 1, если квартира однокомнатная и значение 0, если не однокомнатная;
R2 – фиктивная переменная, которая принимает значение 1, если квартира двухкомнатная и значение 0, если не двухкомнатная;
Если квартира трехкомнатная, то фиктивные переменные R1 и R2 равны нулю.
Переменные z1-z6 – бинарные переменные (могут принимать значения 1 или 0), которые соответствуют различным районам города: z1 принимает значение 1, если квартира расположена в Ворошиловском районе; z2 = 1, если в Дзержинском районе; z3 = 1, если в Кировском; z4 = 1, если в Красноармейском; z5 = 1, если в Краснооктябрьском; z6 = 1, если в Советском. Центральному району соответствует вариант, при котором бинарные переменные z1-z6 равны нулю.
При анализе факторов, влияющих на стоимость квартир, методом наименьших квадратов (МНК) были построены линейные и нелинейные (логарифмические) уравнения множественной регрессии. В случае линейной регрессии результативным признаком является стоимость квартиры price, а в случае нелинейного уравнения объясняемой переменной является натуральный логарифм цены lnprice. Также были оценены квантильные регрессии. На основе 10%-й и 90%-й квантильных регрессий было исследовано, как зависит стоимость дешёвых и дорогих квартир от общей площади. С помощью медианной регрессии изучалось влияние различных факторов на ценообразование квартир на первичном рынке жилой недвижимости.
Обработка статистических данных проводилась с помощью пакетов прикладных программ MS Excel и GRETL.
2. Описательная статистика
В таблице 2 приведены описательные статистики основных показателей, характеризующих квартиры: стоимость квартиры price, цена одного квадратного метра жилья pm, общая площадь TS. Как видно из таблицы, стоимость однокомнатных квартир, попавших в выборку, колеблется от 950,0 тыс. руб. до 3000,0 тыс. руб. Стоимость двухкомнатных и трехкомнатных квартир варьируется, соответственно, от 1498,1 тыс. руб. до 4200,0 тыс. руб. и от 1904,9 тыс. руб. до 7300,0 тыс. руб. Общая площадь квартир, которая предлагается застройщиками, имеет достаточно широкий диапазон, например, для однокомнатных квартир от 29,90 до 63,80 м2. Двухкомнатные квартиры могут иметь общую площадь от 42,34 до 103,80 м2, а трехкомнатные от 62,1 до 139,0 м2. У покупателей, таким образом, есть достаточно широкий выбор квартир: для кого-то важным является количество комнат, а кому-то необходимы просторные комнаты.
Таблица 2. Описательные статистики стоимости квартиры price, стоимости одного квадратного метра квартиры pm, общей площади TS.
| Показатель |
Однокомнатная квартира |
Двухкомнатная квартира |
Трехкомнатные квартиры |
||||||
| pm, тыс. руб./м2 | price, тыс. руб. | TS, м2 | pm, тыс. руб./м2 | price, тыс. руб. | TS, м2 | pm, тыс. руб./м2 | price, тыс. руб. | TS, м2 | |
| Минимум | 27.94 | 950.0 | 29.90 | 29,06 | 1498,1 | 42,34 | 26,11 | 1904,9 | 62,10 |
| Максимум | 66.23 | 3000.0 | 63.80 | 65,30 | 4200,0 | 103,80 | 64,36 | 7300,0 | 139,00 |
| Медиана | 40.87 | 1695.6 | 40.36 | 40,00 | 2525,8 | 61,49 | 40,83 | 3798,0 | 86,00 |
| Среднее | 42.52 | 1799.9 | 42.11 | 40,79 | 2556,5 | 62,42 | 42,03 | 3803,1 | 89,12 |
Таблица 3. Средняя стоимость одного квадратного метра квартиры pm (тыс. руб./м2) в различных районах города Волгограда.
| Район | Однокомнатные квартиры | Двухкомнатные квартиры | Трехкомнатные квартиры |
| Ворошиловский |
50,29 |
48,46 |
46,31 |
| Дзержинский |
44,50 |
41,55 |
41,97 |
| Кировский |
38,43 |
37,18 |
37,45 |
| Красноармейский |
34,15 |
36,11 |
42,60 |
| Краснооктябрьский |
43,25 |
42,18 |
42,58 |
| Советский |
39,20 |
36,21 |
36,75 |
| Центральный |
54,99 |
51,52 |
52,41 |
В таблице 3 приведены данные о средней стоимости 1 м2 общей площади квартиры по семи районам города Волгограда. Можно отметить, что самая высокая стоимость квадратного метра характерна для квартир, расположенных в Центральном районе, что является вполне ожидаемым. Центральный район является самым благоустроенным районом города с развитой инфраструктурой. И поэтому здесь ведется строительство домов, относящихся к жилью с высокой комфортностью и к элитному классу. За Центральным районом следует Ворошиловский. Наиболее низкие цены наблюдаются в Советском, Кировском и Красноармейском районах.
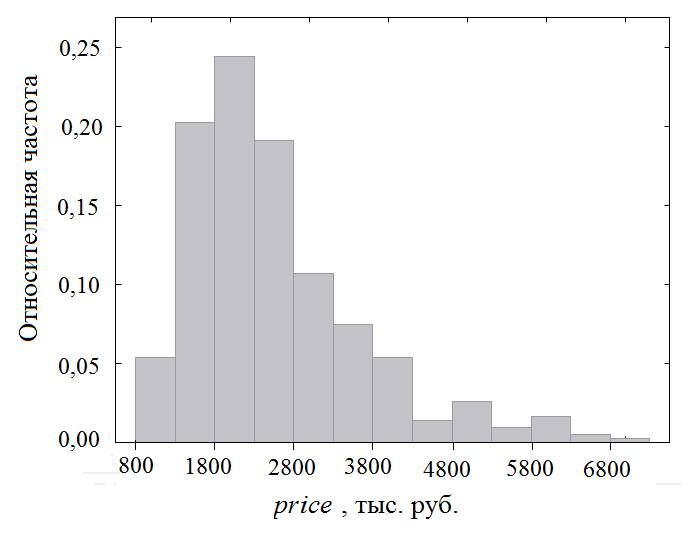
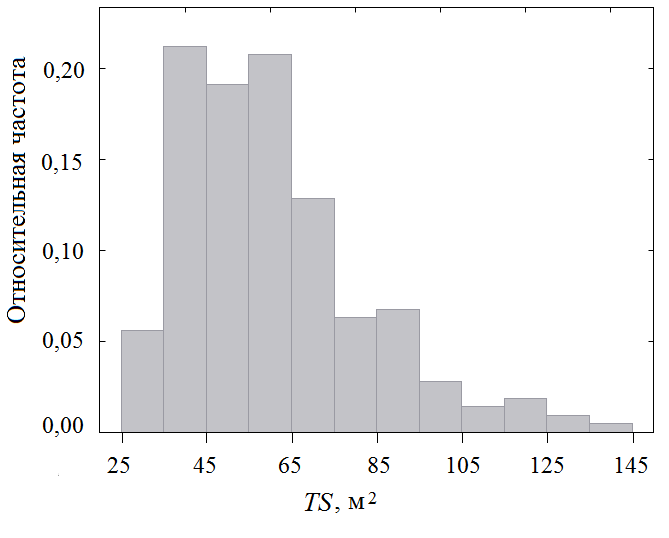
На рис. 1 и 2 представлены гистограммы распределения стоимости квартир и общей площади. Видно, что оба распределения скошены вправо, что является характерным для цен на недвижимость и общей площади квартир.
Рис. 1. Гистограмма распределения цен на квартиры price, тыс. руб.
Рис. 2. Гистограмма распределения общей площади квартиры TS, м2.
3. Уравнения регрессии, построенные методом наименьших квадратов
Для выявления факторов, влияющих на стоимость квартир на первичном рынке жилой недвижимости, проводилась подгонка статистических данных линейными и нелинейными (логарифмическими) уравнениями. При анализе остатков данных моделей было выявлено, что остатки не подчиняются нормальному закону (критерий Пирсона), математическое ожидание равно нулю, наблюдается гетероскедастичность остатков (Тест Уайта). Поэтому, чтобы оценки параметров уравнений регрессии были эффективными, стандартные ошибки оценок были скорректированы с помощью процедуры Уайта (вариант HC0 [5]).
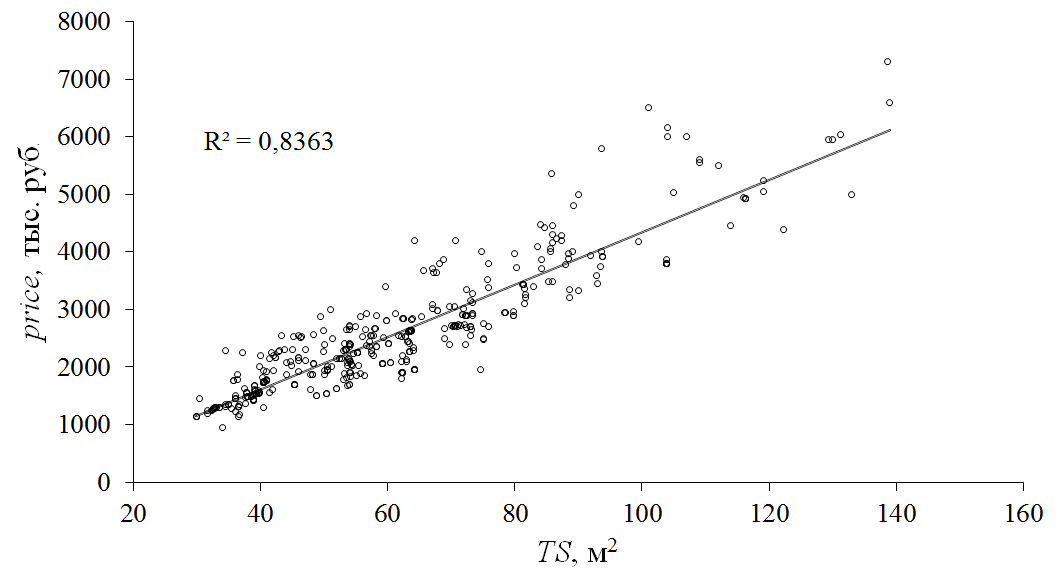
На основе анализа корреляционной матрицы было выявлено, что наибольшая теснота связи с зависимой переменной price наблюдается у переменной TS (выборочный коэффициент корреляции равен 0,914), что является вполне предсказуемым. На рис. 3 показано корреляционное поле в координатах price и TS, а также линейное уравнение регрессии, аппроксимирующее данное распределение.
Рис. 3. Парное линейное уравнение регрессии зависимости стоимости квартиры price от ее общей площади TS.
При построении множественного линейного уравнения регрессии рассматривались несколько моделей с различными комбинациями факторов. Отбор уравнений регрессии проводился на основе исправленного коэффициента детерминации R2adj, F-статистики, t-статистики и критерия Акаике AC. Было выбрано линейное уравнение, у которого все выборочные коэффициенты регрессии статистически значимы (хотя бы на уровне 0,1):
Скорректированный коэффициент детерминации: R2adj ≈0,926, критерий Фишера F(10, 419) ≈ 393,9, критерий Акаике AC ≈ 6111,0.
В таблице 4 приведены основные показатели, характеризующие результаты регрессионного анализа множественного линейного уравнения с зависимой переменной price: стандартные ошибки, P-значения, 95%-й доверительный интервал для выборочных коэффициентов.
Таблица 4. Результаты регрессионного анализа множественного линейного уравнения регрессии с зависимой переменной price, тыс. руб.
| Переменная |
Значение коэффициента |
Стандартная ошибка |
P-значение |
95%-й доверительный интервал |
|
|
Нижняя граница |
Верхняя граница |
||||
|
const |
562,7 |
125,9 |
0,000 |
355,1 |
770,3 |
|
z1 |
-199,2 |
110,7 |
0,072 |
-381,8 |
-16,6 |
|
z2 |
-525,2 |
117,5 |
0,000 |
-719,0 |
-331,4 |
|
z3 |
-853,2 |
91,6 |
0,000 |
-1004,2 |
-702,2 |
|
z4 |
-830,6 |
124,5 |
0,000 |
-1035,9 |
-625,4 |
|
z5 |
-565,0 |
93,8 |
0,000 |
-719,6 |
-410,3 |
|
z6 |
-849,9 |
90,5 |
0,000 |
-999,1 |
-700,8 |
|
R1 |
117,1 |
48,0 |
0,015 |
38,0 |
196,3 |
|
time |
-43,6 |
10,6 |
0,000 |
-61,0 |
-26,2 |
|
BS |
25,7 |
6,2 |
0,000 |
15,4 |
36,9 |
|
TS |
41,6 |
2,0 |
0,000 |
38,6 |
45,1 |
В силу того, что распределения переменных price и TS имеют правостороннюю асимметрию, были рассмотрены регрессионные модели, в которые включены логарифмы данных переменных, т.е. lnprice и lnTS. В результате было получено следующее множественное нелинейное уравнение со значимыми коэффициентами (на уровне 0,1):
Скорректированный коэффициент детерминации: R2adj ≈0,942, критерий Фишера F(9, 419) ≈ 819,2, критерий Акаике AC ≈-807,0.
Основные результаты оценки множественного нелинейного регрессионного уравнения приведены в таблице 5.
Таблица 5. Результаты регрессионного анализа множественного нелинейного уравнения регрессии с зависимой переменной lnprice .
| Переменная | Значение коэффициента | Стандартная ошибка | P-значение |
95%-й доверительный интервал |
|
|
Нижняя граница |
Верхняя граница |
||||
|
const |
4,006 |
0,131 |
0,000 |
3,749 | 4,262 |
|
z2 |
-0,115 |
0,023 |
0,000 |
-0,160 | -0,070 |
|
z3 |
-0,270 |
0,019 |
0,000 |
-0,307 | -0,234 |
|
z4 |
-0,310 |
0,034 |
0,000 |
-0,377 | -0,243 |
|
z5 |
-0,137 |
0,018 |
0,000 |
-0,172 | -0,102 |
|
z6 |
-0,282 |
0,016 |
0,000 |
-0,314 | -0,251 |
|
R1 |
0,044 |
0,017 |
0,008 |
0,011 | 0,077 |
|
time |
-0,018 |
0,003 |
0,000 |
-0,024 | -0,013 |
|
BS |
0,009 |
0,001 |
0,000 |
0,006 | 0,011 |
|
lnTS |
0,971 |
0,032 |
0,000 |
0,910 | 1,033 |
Анализ полученных уравнений на наличие мультиколлинеарности между регрессорами, проводился с помощью метода инфляционных факторов. Коэффициенты инфляции VIFj не превышали четырех. Т.е. можно полагать, что в полученных моделях отсутствует существенная мультиколлинеарность.
На основе таких показателей как R2adj, F-статистика и критерий AC нелинейная модель оказывается более предпочтительной. Однако в этой модели на один фактор меньше, чем в линейной регрессии. Из таблицы 4 видно, что в линейной модели все переменные, соответствующие районам города, статистически значимы. В нелинейной модели (табл. 5) переменная z1, которая соответствует Ворошиловскому району, отсутствует, т.е. оказалась незначимой. При этом в первой модели P-значение коэффициента при z1 равно 0,072. Данный результат можно интерпретировать следующим образом: цены на квартиры в Ворошиловском и Центральном районах отличаются не существенно, и на основе данной выборки нелинейное уравнение не «смогло» выявить данное различие. Для того, чтобы уменьшить P-значение соответствующего коэффициента, необходимо увеличить объем выборки.
На основе коэффициентов при фиктивных переменных z1-z6 линейного уравнения можно ранжировать районы по стоимости квартир на первичном рынке. Поскольку свободный коэффициент положительный, то можно считать, что в Центральном районе расположены самые дорогие квартиры. Затем следует Ворошиловский район, в котором квартиры в среднем уступают в стоимости Центральному району на 199,2 тыс. руб. при прочих равных условиях. На третьем месте находится Дзержинский район, далее Краснооктябрьский, Красноармейский, Советский и, наконец, Кировский район с самыми недорогими квартирами. Ранжирование районов по стоимости квартир с помощью нелинейного уравнения дает немного другую последовательность. На первом месте находятся два района: Ворошиловский и Центральный, затем следуют Дзержинский, Краснооктябрьский, Кировский, Советский и Красноармейский районы.
Из двух фиктивных переменных, показывающих количество комнат в квартирах, значимой в обоих уравнениях оказалась переменная R1. Таким образом, различия в стоимости двухкомнатных и трехкомнатных квартир выявлено не было. Выборочный коэффициент при переменной R1 у нелинейного уравнения показывает, что, если квартира однокомнатная, то это приводит к увеличению стоимости квартиры на 4,4 %.
Общая площадь квартиры TS и площадь балкона BS имеют положительные коэффициенты у двух уравнений. Выборочный коэффициент нелинейной регрессии при факторном признаке BS показывает, что увеличение площади балкона на 1 м2 приводит к увеличению стоимости квартиры на 0,9 %. При увеличении общей площади TS на 1% стоимость квартиры увеличивается на 0,971%.
Коэффициенты при переменной time у линейной и нелинейной модели имеют отрицательный знак. Таким образом, длительный срок сдачи в эксплуатации, наоборот, снижает стоимость квартиры в среднем на 1,8 % при увеличении переменной time на 1 квартал.
4. Квантильные регрессии
Для того, чтобы оценить влияние общей площади TS квартиры на ее стоимость для случаев самых дешевых и самых дорогих квартир, были построены квантильные регрессии. Одно из важных достоинств данного вида регрессий является устойчивость к статистическим выбросам. Кроме того, они позволяют расширить возможности анализа данных. Общая формула уравнения для различных квантилей τ имеет следующий вид:
![]() При оценке параметров квантильной регрессии минимизируется взвешенная сумма модулей:
При оценке параметров квантильной регрессии минимизируется взвешенная сумма модулей:
В дальнейшем 10%-й квантиль будем называть недорогим жильем, а 90%-й квантиль – дорогим жильем.
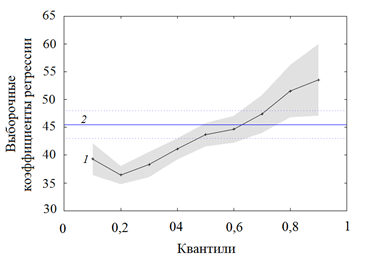
На рис. 4 показано распределение коэффициентов при переменной TS квантильной регрессии для различных квантилей (1). Прямая (2) на данном графике показывает значение коэффициента, полученное МНК. Из рисунка видно, что все коэффициенты квантильной регрессии являются статистически значимыми на уровне 0,05.
Рис. 4. Выборочные коэффициенты при переменной TS квантильной регрессии для различных квантилей распределения с 95%-й доверительным интервалом (1); МНК-оценка с 95%-й доверительным интервалом (2).
Уравнение для недорогих квартир (10%-й квантиль) имеет следующий вид (в скобках указаны стандартные ошибки):
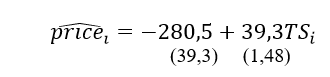 Уравнение для дорогих квартир (90%-й квантиль):
Уравнение для дорогих квартир (90%-й квантиль):
Таким образом, при увеличении площади квартиры на 1 м2 стоимость недорогих квартир увеличивается на 39,3 тыс. руб., а стоимость дорогих – на 53,6 тыс. руб. Для полной картины построим уравнение для медианы, т.е. 50%-го квантиля. Уравнение для медианной регрессии имеет следующий вид:
Данное уравнение показывает, что при увеличении площади на 1 м2 медианное значение цены увеличивается на 43,7 тыс. руб.
На рис. 5 показаны квантильные регрессии зависимости price от TS. Маркеры, залитые красным цветом, отображают элитные квартиры. Как видно из рисунка, основная часть красных точек располагается выше 90%-й квантильной регрессии.
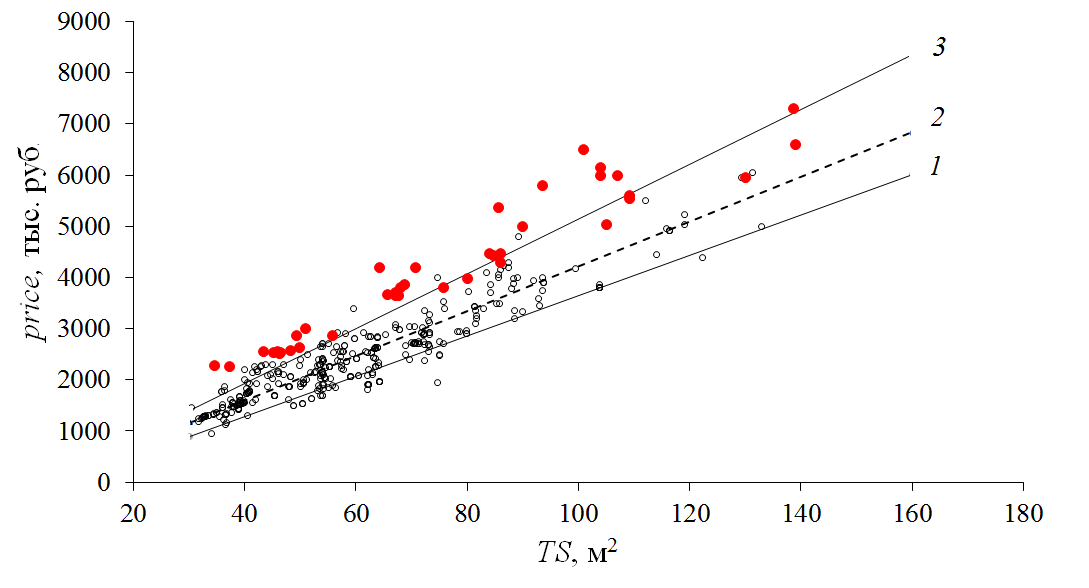 Рис. 5. Квантильные регрессии: 1 – 10%-я квантильная регрессия; 2 – медианная; 3 – 90%-я квантильная регрессия. Маркеры, которые залиты красным цветом, обозначают элитные квартиры.
Рис. 5. Квантильные регрессии: 1 – 10%-я квантильная регрессия; 2 – медианная; 3 – 90%-я квантильная регрессия. Маркеры, которые залиты красным цветом, обозначают элитные квартиры.
Была также построена модель медианной множественной регрессии. В результате анализа выбрано уравнение, в котором коэффициенты значимы на уровне не хуже 0,1. В таблице 6 приведены основные параметры данной модели.
Таблица 6. Параметры медианной множественной регрессии для стоимости квартир price.
| Переменная |
Значение коэффициента |
Стандартная ошибка |
P-значение |
95%-й доверительный интервал |
|
|
Нижняя граница |
Верхняя граница |
||||
|
const |
704,2 |
138,0 |
0,000 |
433,0 |
975,4 |
|
z1 |
-265,7 |
134,9 |
0,049 |
-530,9 |
-0,5 |
|
z2 |
-403,0 |
155,9 |
0,010 |
-709,4 |
-96,6 |
|
z3 |
-834,5 |
127,9 |
0,000 |
-1085,9 |
583,1 |
|
z4 |
-866,0 |
135,4 |
0,000 |
-1132,1 |
-600,0 |
|
z5 |
-644,2 |
134,5 |
0,000 |
-908,7 |
-379,8 |
|
z6 |
-754,4 |
126,9 |
0,000 |
-1003,8 |
-505,1 |
|
R1 |
60,0 |
26,9 |
0,026 |
7,0 |
112,9 |
|
time |
-46,2 |
6,1 |
0,000 |
-58,1 |
-34,3 |
|
BS |
23,0 |
4,6 |
0,000 |
14,0 |
31,9 |
|
TS |
39,2 |
1,1 |
0,000 |
37,0 |
41,4 |
|
brick |
36,7 |
16,5 |
0,026 |
4,3 |
69,1 |
Из таблицы 6 видно, что в медианное уравнение в отличие от моделей, построенных МНК, включена еще одна статистически значимая переменная brick. Это, по всей видимости, объясняется тем, что квантильная регрессия является устойчивой к статистическим выбросам. Ранжирование районов по уровню цен на основе выборочных коэффициентов при фиктивных переменных z1 – z2 дает следующую последовательность: Центральный, Ворошиловский, Дзержинский, Краснооктябрьский, Советский, Кировский, Красноармейский.
Заключение
В результате анализа нескольких видов уравнений регрессии было выявлено, что на стоимость квартиры на первичном рынке жилой недвижимости г. Волгограда оказывают влияние такие количественные признаки как общая площадь, площадь балкона, время до ввода в эксплуатацию жилого дома. Также на стоимость квартиры влияет район города. На основе трех регрессий можно сделать вывод, что самые дорогие квартиры располагаются преимущественно в Центральном и Ворошиловском районах, а недорогие – в Советском, Кировском и Красноармейском. Кроме того, стоимость однокомнатных квартир при прочих равных условиях выше, чем у двух- или трехкомнатных.
Библиографический список
- Дарманян А.П., Филиппов М.В. Прогнозирование стоимости жилищного строительства в России // Бизнес. Образование. Право. Вестник Волгоградского института бизнеса. 2013. № 2 (23). С. 120-123.
- Алпатов А.В., Мещерякова Н.Е., Рубинштейн Е.Ю. Прогнозирование цен реализации жилья на первичном и вторичном рынках города Волгограда в условиях финансового кризиса // Бизнес. Образование. Право. Вестник Волгоградского института бизнеса. 2010. № 2. С. 143-146.
- Катышев П.К., Хакимова Ю.А. Экологические факторы и ценообразование на рынке недвижимости (на примере г. Москвы) // Прикладная эконометрика. 2012. № 4(28). С. 113-123.
- Носов В.В., Цыпин А.П. Эконометрическое моделирование цены однокомнатной квартиры методом географически взвешенной регрессии // Известия Саратовского у-та. Нов. сер. Сер. Экономика. Управление. Право. 2015. Т. 15, вып. 4. С. 381-387.
- Andrew F. Hayes Li Cai. Using heteroskedasticity-consistent standard error estimators in OLS regression: An introduction and software implementation // Behavior Research Methods 2007, 39 (4), P. 709-722.
Количество просмотров публикации: Please wait