Введение понятия производной в школьный курс математики до сих пор вызывает споры между методистами. Одни считают, что производную достаточно изучать только в вузе, другие считают ее введение необходимым. Так, например, Мордкович А.Г. считает, что функциональная линия должна быть ведущей при обучении математике в школе. Вне зависимости от этих разногласий учитель стоит перед необходимостью учить детей элементам анализа. Пропедевтика математического анализа начинается в средней школе, а ключевое понятие математического анализа «производная», вводится в курсе средней школы [3].

Все вышеизложенные противоречия между специалистами, в частности, связаны со сложностями учащихся в усвоении школьниками понятия производной . Для того чтобы овладеть производной учащимся необходимо иметь хорошие представления о бесконечно малых и больших величинах, пределе, приращении функции, дифференцировании и др.

Наше исследование связано с изучением сложившихся тенденций в обучении решению задач, связанных с производной функции в старшей школе и разработки комплекса заданий, способствующих помочь учащимся, учителю в сдаче Единого государственного экзамена.

Для того, чтобы составить представление о типах задач на применение производной в базовом уровне ЕГЭ по математике обратимся к открытому банку заданий Федерального Института Педагогических Измерений (ФИПИ) [1], так как именно он является первоисточником всех заданий ЕГЭ, все остальные, представленные в очень большом количестве электронные и бумажные издания, интернет сайты и так далее составлены на основе именно этого интернет ресурса.

Открытый банк заданий базового уровня ЕГЭ по математике содержит разделы:

- алгебра;

- уравнения и неравенства;

- функции;

- начала математического анализа;

- геометрия;

- элементы комбинаторики, статистики и теории вероятностей.

Задания на применение производной представлены в двух разделах: функции и начала математического анализа, причем какой-то системы по их размещению нет.

Мы полагаем, что для эффективного обучения решению этих задач необходимо разбить их по типам в соответствии с темами, способами решения и необходимыми знаниями для решения.

Для лучшего обзора представим основные типы задач с применением производной в виде таблицы 1.

Таблица 1- Основные типы задач с применением производной

Уровень	Базовый	Профильный
№ задания	14	В8	В12
Типы      задач	Задания на характеристики функции и производной	Задания на определение по графику производной функции свойств функции.	Задания на нахождение точек экстремума функции
	Задания на определение значения производной функции в точке	Задачи на определение по графику функции свойств или значений  производной	Задания на нахождение наименьшего и наибольшего значений функции
		Задания на нахождение по графику функции, с проведенной касательной к точке графика значения производной в этой точке
		Задания на определение по графику функции свойств касательной
		Задания на механический смысл производной функции

Проверяемые требования (умения) в заданиях В8 по кодификатору:

- Определять значение функции по значению аргумента при различных спо­собах задания функции;

- Описывать по графику поведение и свойства функций, находить по графику функции наибольшие и наименьшие значения;

- Строить графики изученных функций;

- Вычислять производные и первообразные элементарных функций;

- Исследовать в простейших случаях функции на монотонность, находить наибольшие и наименьшие значения функций.

Рассмотрим некоторые примеры задач.

•   Подготовка  к решению задачи 14 базового уровня

Пример 1.  На рисунке 1 изображен график функции  и отмечены точки -6, 2. В какой из этих точек значение производной наименьшее? В ответе укажите эту точку.

 

Рисунок 1

Алгоритм решения задач на определение значения производной в точке по графику

1. Определить в каких точках графика касательная возрастает
2. Распределить данные в ответе положительные значения по правилу: чем «круче возрастает касательная», тем больше значение
3. Определить в каких точках графика касательная убывает
4. Распределить данные в ответе отрицательные значения по правилу: чем «круче убывает касательная», тем меньше значение
5. В точках, в которых касательная параллельна оси абсцисс или совпадает с ней, значение производной равно нулю

•     Геометрический смысл производной

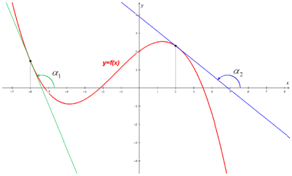
Пример 2. Найдите значение параметра, при котором прямая  будет являться касательной к графику функции  .

Решение представлено рисунке 2.

Рисунок 2 – Решение примера 2

Алгоритм решения задачи с параметрами на геометрический  смысл производной

1. Найти производную функции
2. Найти угловой коэффициент   касательной по ее уравнению
3. Найти абсциссу точки касания, для этого решить уравнение
4. Подставить, найденное значение  в уравнения касательной или функции и найти значения параметров

•  Физический смысл производной функции

Пример 3. Материальная точка движется прямолинейно по закону  , где  — расстояние от точки отсчета в метрах,  — время в секундах, измеренное с начала движения. Найдите расстояние, пройденное точкой от начала движения до остановки.

Решение. Найдем момент времени, когда скорость точки равна нулю. Так как , то из уравнения  находим . Тогда искомое расстояние равно  (м).

Ответ:  25 м.

Таблица 2  – Алгоритм решения задачи на физический  смысл производной

1. Определить, что надо найти в задаче
Расстояние от начала движения	Скорость	Время
2. Найти производную функции
3. Найти время остановки, для этого решить уравнение 4. Подставить найденное значение  в	3. Подставить значение  в	3. Подставить значение  в 4. Решить уравнение, найти t

•  Промежутки монотонности

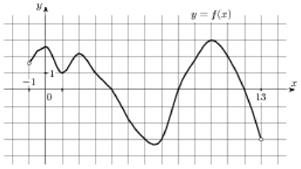
Пример 4. На рисунке 3 изображен график функции , определённой на интервале (—1; 13). Определите количество целых точек, в которых производная функции положительна.

Рисунок 3

Алгоритм решения задачи на нахождение по графику функции  количества целых точек, в которых производная положительная (отрицательная, равна нулю)

1. Если необходимо найти точки, в которых производная положительная, выбрать из указанных на графике точек те, в которых функция возрастает;
2. Если необходимо найти точки, в которых производная отрицательная, выбрать из указанных на графике точек те, в которых функция убывает;
3. Если необходимо найти точки, в которых производная равна 0, выбрать из указанных на графике точек те, в которых функция имеет экстремум.
4. Посчитать количество этих точек.

•    Точки экстремума

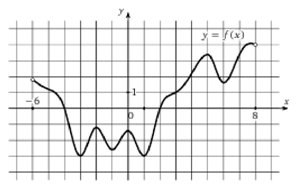
Пример 5. На рисунке 4 изображен график функции , определенной на интервале (-6;8). Найдите: а) количество точек, в которых касательная к графику функции  параллельна прямой y = -1000000; б) сумму точек экстремума функции  .

Рисунок 4

Алгоритм решения задания на точки экстремума (точки, в которых касательная к графику функции параллельна прямым вида )

1. Найти точки экстремума функции (экстремум –это абсцисса );
2. Выбрать те, которые принадлежат указанному интервалу
3. Если необходимо сложить их значения

•   Промежутки монотонности

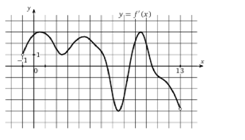
Пример 6. На рисунке 5 изображен график  - производной функции , определенной на интервале (—1; 13). Найдите промежутки возрастания функции  . В ответе укажите сумму целых точек, входящих в эти промежутки.

Рисунок 5

Алгоритм решения зада на нахождение промежутков возрастания (убывания) функции по графику производной

1. Если необходимо найти промежутки возрастания функции, то на графике производной ищем промежутки, в которых производная положительная, то есть график расположен выше оси абсцисс
2. Если необходимо найти промежутки убывания функции, то на графике производной ищем промежутки, в которых производная отрицательная, то есть график расположен ниже оси абсцисс
3. Находим сумму целых значений x из этих промежутков, либо находим длину наибольшего (наименьшего) из промежутков, либо количество этих точек.

Анализ школьных учебников, учебных пособий и научно-методической литературы по проблеме исследования показал, что несмотря на то, что теоретические знания и практические умения на тему производной необходимы для решения одной задачи базового и двух задач профильного уровня в школьной литературе не только нет выделенного блока таких заданий, но и вообще отсутствуют прототипы некоторых заданий, что в свою очередь затрудняет подготовку к ЕГЭ.

В открытом банке задания на производную ФИПИ расположены в хаотичном порядке, их изучение позволило нам разделить их на типы по содержанию и способу решения.

Подробный разбор каждого типа заданий на производную, позволил выделить различные приемы и способы решения задач на производную, а также выявить в них «подводные камни», «задачи-ловушки» и так далее.

Изучение элементов математического анализа в школе имеет несомненную важность в развитии представлений учащихся о структуре математики и ее приложений. Именно приложения производной, ее геометрическое и механическое толкования и являются принципиальными при формировании содержания задач ЕГЭ. Это вопросы применения производной в исследовании функций, в прикладных задачах и определение по графику производной свойств функции, а также обратная задача.

Систему упражнений для подготовки к ЕГЭ рекомендовано строить так, чтобы она способствовала систематизации основополагающих понятий, давала новое видение изученного материала и  его качественное усвоение.

В нашей работе мы выделили основные типы задач, содержащихся в открытом банке заданий ФИПИ ЕГЭ, обратили внимание на сложности в  их решении, рассмотрели требования ФГОС и ЕГЭ, провели анализ учебных пособий и задач ЕГЭ по математическому анализу, составили систему задач, дающую представление учащимся и учителю, о предлагаемых задачах на ЕГЭ. Таким образом, задачи исследовательской работы выполнены.

Библиографический список

1. Федеральный институт педагогических измерений [Электронный ресурс] URL: http://www.fipi.ru/. Режим доступа: (Дата обращения: 9.06.2016).
2. Стандарты образования. Электронный журнал об образовании и воспитании [Электронный ресурс] URL:  http://www.edustandart.ru. Режим доступа: (Дата обращения: 19.05.2016).
3. Мордкович А.Г. Алгебра и начала анализа. 10 – 11 классы./Задачник для общеобразовательных учреждений /- 8-е изд., стер. – М., Мнемозина,- 2007. – С315.
4. Мордкович А.Г. Беседы с учителями математики: концептуальная мето­дика, рекомендации, советы, замечания. Обучение через задачи /- М., Школа-Пресс, -1999. – С272.
5. Стандарты образования. Электронный журнал об образовании и воспитании [Электронный ресурс] URL:  http://www.edustandart.ru. Режим доступа: (Дата обращения: 19.05.2016).

---

Количество просмотров публикации: Please wait

Все статьи автора «Габитова Альбина Ринатовна»