Факторный анализ (ФА), как метод интерпретации, позволяющий придать содержательный смысл результатам исследования, имеющим числовую природу, нашел широкое применение во многих областях научных исследований [1 - 4]. Так, например, в психологии рассматриваемый метод применяется для изучения свойств личности, её поведения с помощью ответов на вопросы психологических тестов [1]. В социологии факторный анализ активно применяется для обработки результатов анкетирования, которое является одним из основных инструментов изучения состояния общественного мнения [2].

Такая популярность метода объясняется в первую очередь тем, что он реализован в прикладных программах статистической обработки данных, например, таких, как SPSS и STATISTICA. Вследствие чего, пользователи, не имеющие специальной математической подготовки и не владеющие математическим аппаратом метода, но понимающие его назначение, сущность и возможности могут использовать факторный анализ в своих исследованиях.

Тем не менее, метод имеет ряд ограничений, которые, главным образом, связаны с метризуемостью пространства исходных переменных. Для адекватного применения метода ФА необходимо точно определить тип шкалы, в которой они были измерены.

В связи с этим проблема применимости метода для обработки таблиц с результатами анкетирования, данные в которых представлены в порядковых, номинальных и дихотомических шкалах является актуальной.

Согласно алгоритму метода процедура ФА включает в себя следующие этапы:

1. Построение корреляционной матрицы системы переменных с использованием коэффициента линейной корреляции Пирсона;

2. Определение новых признаков, являющихся линейными комбинациями первоначальных и включающих в себя большую часть общей дисперсии наблюдаемых данных. Этот этап реализуется с использованием методов главных компонент, главных факторов, максимального правдоподобия и других [4 - 6].

3. В случае, если выделенные факторы, невозможно достаточно наглядно интерпретировать, то используют их вращение, позволяющее найти более наглядное объяснение факторной структуры [4 - 6].

Таким образом, в основе процедуры факторного анализа лежит этап построения матрицы коэффициентов линейной корреляции Пирсона, которая и определяет в дальнейшем процесс выделения новых латентных переменных, а, следовательно, и содержательный смысл исходных данных. В свою очередь, коэффициент линейной корреляции Пирсона рассчитывается только для нормально распределенных данных, представленных в интервальной шкале.

Однако, при обработке результатов анкетирования, часто приходится иметь дело с порядковыми, номинальными и дихотомическими шкалами. Например, респондентам предлагается оценить предложенные суждения по шкале Р. Лайкерта, содержащей несколько градаций (3, 5, 7, 9 и т.д.) или выразить свое отношение к проблеме одним из высказываний – «согласен»-«не согласен», «да»-«нет».

В связи с этим возникает вопрос о правомерности применения метода для обработки результатов анкетирования. Т.е. правомерно ли использовать ФА для исследования структуры данных, представленных в порядковой, номинальной и дихотомической шкале.

Включение в исследование порядковых переменных будет зависеть от балльности шкалы. В зависимости от количества используемых баллов порядковые шкалы условно можно разделить на шкалы с низким и высоким числом градаций. Установлено, что шкалы с 5-ю градациями и выше, обладают свойствами как порядковых, так и интервальных шкал [6, 7], иначе говоря, являются псевдо-интервальными. Переменные, измеренные в таких шкалах, допустимо использовать в качестве исходных данных для процедуры ФА. Причем чем больше выбор ответов на порядковой шкале, тем ниже вероятность серьезных ошибок при интерпретации результатов. Тем не менее, перед применением метода рекомендуется проводить предварительный этап анализа корреляционной зависимости между переменными. Для этого сравниваются матрицы коэффициентов корреляции, рассчитанные для переменных таблицы исходных данных по формулам Пирсона и Спирмена (или Кендалла). Если расхождение между элементами матриц незначительны, то есть искажения, полученные из-за шкалирования не слишком велики, то использование ФА является правомерным. В свою очередь шкалы с низким числом градаций не обладают свойствами интервальных, кроме того, данные, измеренные в таких шкалах, нарушают допущение о нормальности, а, следовательно, не могут служить базой для проведения ФА, т.к. его результаты могут привести к получению ошибок в факторном решении, а, следовательно, к неверным выводам.

При использовании номинальных шкал каждый объект исследования относится к определенной группе (например, при ответе на вопрос об образовании респондент выбирает один из вариантов: 1 – высшее, 2 – среднее специальное, 3 – среднее). То есть номинальная шкала представляет собой конечный набор состояний или свойств объекта. Для нее невозможно установить отношение порядка, нулевую точку и интервальность. Следовательно, коэффициент линейной корреляции Пирсона нельзя использовать в качестве характеристики зависимости между переменными, классифицированными по этой шкале. Таким образом, применение ФА для номинальных переменных невозможно.

В случае анализа дихотомических переменных, следует отметить, что согласно сущности метода, каждая переменная оказывается под влияние двух типов факторов – общего и частного:

,

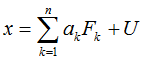где

x – переменная,

n – количество факторов,

k – номер фактора (k=1,…n),

F_k – общий фактор,

U – частный фактор.

Если предположить, что k=1 и факторы F и U принимают только два значения, то итоговые переменные должны принимать, четыре различных значения, что приводит к противоречивости использования дихотомических переменных в качестве исходных данных для анализа [5]. Кроме того, дихотомические переменные значительно ослабляют коэффициент линейной корреляции Пирсона. Поэтому применение метода для их анализа данных невозможно [5].

Необходимо отметить, что в общем случае все переменные, для которых проводится ФА, должны быть измерены в одной шкале. Тем не менее, на практике это требование в большинстве случаев не выполняется. Если в таблице исходных данных преобладают интервальные и ранговые переменные с большим числом градаций, то применение ФА является обоснованным. Тем не менее, нужно учитывать возможное искажение факторной структуры, связанное с искажение коэффициента корреляции.

Несмотря на все ограничения для исходных данных, некоторые исследователи говорят о допустимости применения ФА в отношении порядковых и номинальных переменных в эвристических целях, при условии получения простой факторной структуры и высоких значений факторных нагрузок переменных, определяющих каждый фактор [5, 6].

Подводя итог, можно сделать следующие выводы о возможности использования ФА для обработки результатов анкетирования. Применение метода считается правомерным, если он используется для анализа переменных, измеренных в интервальной шкале или в порядковой с большим числом градаций и имеющих согласованные матрицы корреляции, построенные с использованием коэффициента линейной корреляции Пирсон и Спирмена (или Кендалла).

Использование ФА для обработки порядковых переменных с низким числом градаций, номинальных или дихотомических переменных может привести к получению искаженной информации, которая на самом деле не содержится в данных и, как следствие, к получению неверных выводов. Анализ таких переменных осуществляется с применением других методов, в частности нелинейного метода главных компонент, не накладывающего ограничений на тип используемой шкалы.

1. Митина О. В., Михайловская И.Б. Факторный анализ для психологов. – М.: Учебно-методический коллектор «Психология». – 2001. – 169 с.
2. Фомина Е. Е. Применение факторного анализа для обработки результатов анкетирования // Социосфера. – 2016. – № 3. – С. 122-127.
3. Самсонова А. В. Факторный анализ. Направления применения и неиспользованные возможности // Вестник Балтийской Педагогической Академии. – 2005. – вып. 62. – С. 67-75.
4. Буреева Н. Н. Многомерный статистический анализ с использованием ППП «STATISTICA». Учебно-методический материал по программе повышения квалификации «Применение программных средств в научных исследованиях и преподавании математики и механики». – Нижний Новгород. – 2007. – 112 с.
5. Факторный, дискриминантный и кластерный анализ: Пер. с англ. / Дж.-О. Ким, Ч. У. Мьюллер, У. Р. Клекка и др.; Под ред. И. С. Енюкова. – М.: Финансы и статистика.  – 1989. – 215 с.
6. Иберла К. Факторный анализ / Пер. с нем. В.М. Ивановой; Предисл. А.М. Дуброва. – М.: Статистика. – 1980. – 389 с.
7. Толстова Ю. Н. Измерение в социологии. – М.: КДУ. – 2007. – 288 с.

Все статьи автора «Фомина Елена Евгеньевна»