Захарова О.И., научный руководитель, кандидат технических наук,
доцент кафедры «Информационные системы и технологии»
Поволжский государственный университет телекоммуникаций и информатики
При изучении объектов, характеризуемых большим числом факторов, часто бывает важно определить, какие из этих факторов в большей степени влияют на интересующие нас свойства объектов.
Предварительная оценка значимости факторов может быть сделана на основе логического анализа, научных исследований или интуитивно. Однако более точно поставленная задача может быть решена на основе вычисления оценки информационной значимости факторов, которая дает возможность количественно определить степень их значимости.
Применительно к распознаванию образов информативность фактора – это оценка количества информации, которую несет в себе фактор о принадлежности объекта к тому или иному классу.
Таким образом, информативным и мы будем считать те факторы, информативность которых превышает заданное критическое значение. Если же информативность фактора меньше этого критического значения, то этот фактор неинформативный (или малоинформативный).
Количество информации является мерой, которая характеризует значимость фактора с точки зрения распознавания. В то же время количество информации не имеет никакой связи с обще надежностью распознавания и не зависит от правила решения, используемого распознавания системой.
Иногда при небольших изменениях режима эксплуатации объектов информативный фактор может стать либо малоинформативным, либо вообще неинформативным, это показывает неполноту наших знаний о степени неустойчивости процессов, ведущих к появлению отказов. Выход из этого положения один – детальное исследование реальных физических процессов, лежащих в основе развития отказов.
Информативность фактора может быть оценена различными критериями.
Рассмотрим несколько из них:критерий Шеннона;
критерий Пирсона;
критерий Фишера.Критерий Шеннона - предполагает оценивать информативность как средневзвешенное количество информации, приходящиеся на различные градации признака. Под информацией в теории информации понимают величину устраненной энтропии.
Итак, информативность j – ого признака:
где G - количество градаций признака; K - количество классов; ![]() - вероятность i-той градации признака.
- вероятность i-той градации признака.
 , где
, где ![]() - частота появления i-той градации в K - том классе; N - общее число наблюдений.
- частота появления i-той градации в K - том классе; N - общее число наблюдений.
![]() - вероятность появления i-той градации признака в K - том классе
- вероятность появления i-той градации признака в K - том классе
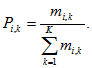
Пример:
При анализе кредитоспособности заемщиков банка важное значение имеет работает человек или нет. Так как этот признак относится к качественно информации, то для его обработки применяется прием условного кодирования. В данном случае – альтернативного кодирования, то есть такого, при котором признак может принимать одно из двух возможных значении: 0 – кредит не одобрен, 1 – кредит одобрен. Было проанализировано 20 человек, из которых у 9 – высшее образование, а у 11 – средне – специальное. Результат приведен в Таблице 1.
Таблица 1 – Исходные данные
|
Номер градации признака i
|
Значения градации
|
Номер класса
|
|
|
1(высшее образование)
|
2(средне – специальное образование)
|
||
|
Частоты появления градаций
|
|||
|
1
|
0
|
4
|
9
|
|
2
|
1
|
5
|
2
|
Подсчитаем информативность по критерию Шеннона:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Значение информативности:
![]()
Определение информативности по χ2 - критерию Пирсона. Предположим, что выполнено n измерений некоторой случайной величины ![]() :
: ![]() ,(1). И есть основание полагать, что результаты распределены нормально с плотностью вероятности
,(1). И есть основание полагать, что результаты распределены нормально с плотностью вероятности
.gif)
Параметры закона распределения m и ![]() обычно неизвестны. Вместо неизвестных параметров подставляют значения их оценок, которые вычисляются по следующим формулам:
обычно неизвестны. Вместо неизвестных параметров подставляют значения их оценок, которые вычисляются по следующим формулам:
![]()
.gif)
В качестве критерия проверки выдвинутой гипотезы примем критерий согласия Пирсона (критерий согласия “ χ2 ”)
![]()
Где k – число интервалов, на которое разбито выборочное распределение, ![]() - частоты эмпирического распределения;
- частоты эмпирического распределения; ![]() - частоты теоретического распределения. Из формулы вытекает, что критерий характеризует близость эмпирического и теоретического распределений: чем меньше различаются
- частоты теоретического распределения. Из формулы вытекает, что критерий характеризует близость эмпирического и теоретического распределений: чем меньше различаются ![]() и
и ![]() , тем меньше значение
, тем меньше значение ![]() . Доказано, что при
. Доказано, что при ![]() закон распределения случайной величины(5) независимо от того, какому закону распределения подчинена генеральная совокупность, стремится к закону распределения
закон распределения случайной величины(5) независимо от того, какому закону распределения подчинена генеральная совокупность, стремится к закону распределения ![]() с r степенями свободы.
с r степенями свободы.
Пример: Проверить с помощью критерия χ2 при уровне значимости 0,05 гипотезу о том, что выборка объема n = 20, представленная интервальным вариационным рядом в таблице 2, извлечена из нормальной генеральной совокупности.
Таблица 2 – Исходные данные
| Номер Интервала I |
Границы Интервала |
Частота |
| 1 | 0 – 2 | 9 |
| 2 | 2 – 4 | 11 |
1. Сформулируем нулевую и альтернативную гипотезы: Н0 - эмпирическое распределение соответствует нормальному, Н1 - эмпирическое распределение не соответствует нормальному.
Для проверки нулевой гипотезы необходимо рассчитать наблюдаемое значение критерия χ2набл по формуле и сравнить его с критическим значением χ2кр.
2. Определим параметры предполагаемого (теоретического) нормального закона распределения.
Найдем середины интервалов ![]() и относительные частоты
и относительные частоты ![]() . Получим следующие значения:
. Получим следующие значения:
| 1 | 3 | |
Найдем оценку математического ожидания:
![]()
Вычислим оценки дисперсии и стандартного отклонения:
![]()
![]()
Выполним расчет теоретических частот ![]() .
.
Последовательно находим для интервала (-8, 2)
![]()
![]()
Для интервала (2, 4) находим
![]()
![]()
4. Найдем значение χ2набл

Поскольку ![]() (24,51>6,0), то можно считать, что гипотеза о нормальном распределении генеральной совокупности противоречит опытным данным.
(24,51>6,0), то можно считать, что гипотеза о нормальном распределении генеральной совокупности противоречит опытным данным.
Определение информативности по F-критерию Фишера основано на степени различия дисперсий значений фактора в выборках класса A и класса B. Если дисперсия фактора, характеризующего объекты класса A - 2AS существенно не отличается от дисперсии значений фактора у объектов класса B - 2BS , то можно сделать вывод о том, что данные совокупности объектов мало чем отличаются друг от друга. В этом случае фактор признается малоинформативным для распознавания.
Для проверки гипотезы H0: 2 2A B S = S вычисляется контрольная величина F.
.gif)
Вычисленное значение F сравнивается с табличным значением Fтаб(K1, K2), где K1и K2 – число степеней свободы соответственно большей и меньшей дисперсий (K=N-1).Если F =Fтаб, гипотеза H0 отвергается, фактор информативен. Если F <Fтаб, фактор неинформативен.
В результате предварительного выбора некоторой совокупности признаков и Определения их вероятностных характеристик, а также распределения вероятностей классов имеется наиболее полное описание каждого из классов. Однако такое полное описание для распознавания может не потребоваться. С одной стороны оно может содержать большую избыточность, с другой – иметь ненужные с точки зрения распознавания сведения.
Поэтому возникает задача минимизации признакового пространства. Она представляет собой количественный анализ полученных вероятностных характеристик и окончательное определение совокупности признаков, которые необходимо использовать в процессе распознавания. Основную роль здесь играет то количество информации, которое несет каждый признак. При этом задача минимизации состоит в том, чтобы найти минимальное количество признаков, обеспечивающих заданную надежность распознавания. Это сократит время распознавания и позволит упростить конструкцию распознающей системы.
Количество просмотров публикации: Please wait


