Применение компьютера для определения времени простой психофизиологической реакции [1, с.70; 2, с.232; 3, с.8] позволяет гибко изменять условия эксперимента. В частности, нами было показано, что простая психофизиологическая реакция на раздражение (ППФР) зависит от результата предварительного раздражения [3, с.8-9], т.е. реакция на раздражение сильно замедляется, если раздражение произошло непосредственно за предыдущей реакцией, и тем больше, чем ближе за предыдущей реакцией было следующее раздражение. По-видимому, мы имеем дело с торможением простой психофизиологической реакции (ТППФР). Это некая аналогия торможения возврата внимания [4, с.42-43]. Мы предположили, исходя из общих соображений, что это торможение спадает экспоненциально, по мере восстановления реагировать на следующее раздражение. В сообщении [3, с.8-9] было продемонстрировано, что спад торможения ТППФР имеет многокомпонентный характер. Однако это предположение имело предварительный характер.
В нашем следующем сообщении мы попытались смоделировать зависимость ТППФР от предварительного времени ожидании на примере анализа зашумленного экспоненциального спада и выяснили, что эта зависимость может быть достаточно легко идентифицирована в виде суммы экспонент, при этом влияние шума можно в значительной степени нивелировать без потери точности [5, c.70].
В настоящем сообщении мы представляем результаты анализа реальной зависимости ТППФР от интервала ожидания. Ход эксперимента проводился следующим образом: испытуемому подавался световой раздражитель. В ответ на это испытуемый реагировал нажатием кнопки мыши. Затем цикл повторялся, причем задавалось время от нажатия кнопки предыдущего нажатия до появления данного сигнала (время ожидания) и время от появления данного сигнала до нажатия кнопки как реакция на данные сигнал (время ППФР). На Рис. 1 изображена зависимость величины времени реакции ППФР от величины предварительного ожидания (интервала времени от предварительной реакции на раздражитель). Как мы видим из Рис. 1, значения величины времени ППФР сильно изменяются в зависимости от того, каков интервал времени от предыдущего реагирования был задан (ромбики), причем на первое место выходит очень большой разброс. Однако есть способ значительного улучшения этой зависимости. В работе [6, с.99-101] Кукиновым А.М. математически строго было доказано, что, при наличии монотонно уменьшающейся зависимости, экспериментальные данные можно упорядочить по рангу, формируя новую зависимость, монотонно уменьшающуюся, (т.е. расположить значения времени реакции в порядке уменьшения) которая будет в результате наиболее близка к истинной зависимости.
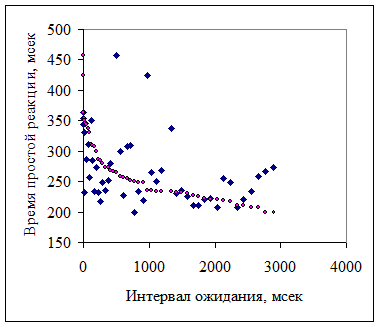
Рис. 1 Зависимость времени простой реакции от временного интервала после предварительного реагирования. Большие ромбики – реальное расположение значений, маленькие кружки – порядковое ранжирование значений времени реакции по мере уменьшения значений.
Мы поступили таким образом, и результирующая зависимость (маленькие кружки) дают нам кривую, спадающую со временем ожидания, причем она сначала уменьшается быстро, а потом все медленнее, в пределе стремясь к какой-то постоянной величине. Основанием для такой перестановки было вычисление в соответствии с [6, с. 106] критерия Кендала, который оказался равным 0,31, и достоверность утверждения, что данная зависимость была монотонно уменьшающейся, оказалась равна 0,998, откуда можно было утверждать, что наше предположение о монотонном уменьшении верно. Таким образом, наше утверждение, что время реакции на раздражение зависит от интервала времени от предыдущего реагирования, и снижается с увеличением этого интервала, достаточно подтверждено, и мы имеем право говорить о торможении ТППФР после реакции на раздражение.
Далее нам предстоит выяснить характер зависимости ТППФР от предварительного реагирования. Кукинов [6, с.102-106] предлагает несколько вариантов дальнейшего улучшения экспериментальной зависимости, кроме простого ранжирования значений. Мы в работе [5, с.68-70] проверили эти варианты и пришли к выводу, что наиболее подходящим являются: 1- упорядочение по рангу экспериментальных данных, 2- замена последних точек на кривой, которая после определенного снижения наклона, вновь быстро начинает снижаться, постоянными величинами, равными точке, с которой началась замена, 3- сглаживание кривой по 3 точкам [7, с.144-145], 4- нахождение значений 1 производной с дальнейшим ранжированием полученных значений и 5- обратное восстановление зависимости с использованием ранжированных значений производной.
В качестве модели поведения мы приняли зависимость, описываемую уравненим (1):
где Yt =время ППФР в текущий момент времени, t – текущий момент времени от предыдущей ППФР, Ao –постоянная величина ППФР в момент времени, бесконечный от предыдущей реакции ППФР, A1, A3 ,A5 – амплитуды 1,2,3 компонент спада торможения ППФР; A2, A4 , A6, – константы спада соответственно 1,2,3 компонент торможения ППФР.
Экспериментальные данные сравнивались с моделью, и вычислялась сумма квадратичных отклонений R2:
R2=(Yi эксп - Yi выч)*(Yi эксп - Yi выч) (2),
где Yi эксп - эксперименальное значение времени ППФР, Y выч – вычисленное из модели (1) значение ППФР. Критерием подбора решения с помощью метода оптимизации была минимальная величина R2. Оптимизация проводилась путем подбора значений амплитуд и коэффициентов уравнения (1) с помощью программы «Поиск решения» в EXCEL. Результаты приведены в Таблице 1.
| № | Характеристики изменений данных | Параметры зависимости, мсек | R2 | ||||||
| A1 | A2 | A3 | A4 | A5 | A6 | Ao | |||
| 1 | Реальные значения | 77,8 | 5,2 | 30,8 | 91,6 | 61,3 | 3133,8 | 193,1 | 188665,6 |
| 2 | Упорядоченные по рангу значения | 179,1 | 1,2 | 115,6 | 202,7 | 148,0 | 4704,4 | 74,2 | 622,2 |
| 3 | Упорядоченные по рангу значения с отсечкой резкого спада последних значений | 181,0 | 1,1 | 107,6 | 187,8 | 18,9 | 834,9 | 211,8 | 655,8 |
| 4 | Как 3, сглаженные данные, 3 компоненты | 133,9 | 2,6 | 110,4 | 210,2 | 10,9 | 695,9 | 215,4 | 519,3 |
| 5 | Как 3, сглаженные, 2 компоненты | 133,9 | 2,6 | 118,5 | 231,2 | - | - | 214,0 | 529,9 |
| 6 | Как 3, сглаженные, 1 компонента | 163,7 | 105,4 | - | - | - | - | 225, | 10223,7 |
| 7 | Как 4, но с упорядочением по рангу производной, 3 компоненты | 181,5 | 0,9 | 64,5 | 25,7 | 106,5 | 393,6 | 181,7 | 58,6 |
| 8 | Как 4, но с упорядочением по рангу производной, 2 компоненты | 149,7 | 3,4 | 125,6 | 284,9 | - | - | 185,6 | 664,8 |
| 9 | Как 4, но с упорядочением по рангу производной, 1 компонента | 180,6 | 99,9 | - | - | - | - | 199,7 | 10639,9 |
Проанализируем Таблицу 1. Аппроксимация экспериментальных точек по уравнению (1) дает нам 3 компоненты с резко отличными компонентами: времена релаксации равны 1,2, 202 и 3130 мсек. (№1). При этом величина Ao, т.е. величина времени реакции при бесконечно большом интервале времени ожидания составляет 193 мсек. Однако величина ошибки R2 составляет очень большую величину, что не позволяет принимать полученные данные достоверными. Упорядочение приводит к резкому снижению R2, как это и указывалось в статье [6]. Полученные значения кинетических констант значительно отличаются от №1. Между тем, у данного испытуемого при задании постоянно как можно быстрее подряд несколько раз нажимать на кнопку реагирования временной интервал между нажатиями составлял примерно 150 мсек., и этот факт находится в противоречии с величиной А0=74,2 мсек в варианте 2.
Таким образом, кроме простого упорядочения по рангу необходимы дополнительные манипуляции. Мы уже говорили, что при упорядочении данных в области больших времен ожидания наблюдается новое увеличение спада ППФР. Это связано как с наличием ошибочных тестов, когда испытуемый реагирует даже быстрее подачи раздражения, так и наличием флуктуаций в реагировании. В результате упорядочения по мере увеличения интервала ожидания происходит быстрое снижение времени ППФР, затем замедление этого снижения, а потом наблюдается вновь увеличение снижения. Такая картина наблюдалась и в модельном эксперименте, когда анализировался зашумленный экспоненциальный спад [5, с.70]. Поэтому мы, начиная с точки нового увеличения скорости снижения данных в кривой зависимости времени ППФР от интервала ожидания, фиксировали дальнейшие точки на том же уровне. В строке №3 показаны результаты итераций в этом случае. Величина R2 почти не изменяется по сравнению со строкой №2, что указывает примерно на тот же характер достоверности, что и в случае простого упорядочения. Амплитуды быстрых компонент насколько уменьшаются, времена релаксации близки к №2. Значительно изменяется медленная компонента: резко уменьшается амплитуда и время релаксации.
Следующим моментом манипуляций данных является сглаживание кривой, как это мы указывали ранее. И эта манипуляция снижает величину R2 с 655 до 519, даже лучше чем в случае простого ранжирования данных (строка № 4). Значения кинетических величин остаются в том же диапазоне, что и у № 3, только медленная компонента становится быстрее.
Следующие строки, №№ 5 и 6, в качестве моделей представляли собой 2- и 1- компонентные спады. Это привело к изменению кинетических параметров, но и к увеличению ошибки, а это свидетельствует о меньшей достоверности результата. Таким образом, наши данные указывают о многокомпонентности ТППРФ.
В попытке приблизить результаты к истинным, мы использовали метод, предложенный Кукиновым [6,с.102-106]: вычисление производных, ран-жирование этих величин и воссоздание с их использованием новой зависимости. Эти данные показаны в строках №№ 7-9 аналогичных строкам №№ 5-7 в отношениях числа компонент. В результате мы видим аналогию в поведении ошибки: она наименьшая в случае модели с 3 компонентами спада ТППФР, что также подтверждает многокомпонентность ТППФР. При этом значения R2 становятся совсем маленькими: 58,6 против 519 у аналогичного варианта. Однако при этом наблюдается резкое снижение времен релаксаций всех трех компонент. При этом кинетики спада ТППФР снижаются гораздо быстрее, чем в случае простого упорядочения, а ведь это – наиболее близкая к истине зависимость. При анализе данных изменений, мы пришли к выводу, что получается это по следующей причине. На рис. 1 видно, что упорядоченная по рангу зависимость представляет собой монотонную, но не совсем гладкую кривую: наблюдаются резкие ступеньки. При упорядочении значений 1-й производной все эти резкие ступеньки перемещаются влево, смещая в целом всю кривую влево. Таким образом, ![]() происходит видимое ускорение спада. По этой причине, несмотря на кажущееся уменьшение R2, мы пришли к выводу о том, что этот подход неверен. Другой подход Кукинова [6,с.102-106], порядковое приближение с использованием рангов, улучшения не принесло. В результате происходило сильное понижение левой части зависимости, выпрямление экспоненциального спада, приближение к прямому спаду.
происходит видимое ускорение спада. По этой причине, несмотря на кажущееся уменьшение R2, мы пришли к выводу о том, что этот подход неверен. Другой подход Кукинова [6,с.102-106], порядковое приближение с использованием рангов, улучшения не принесло. В результате происходило сильное понижение левой части зависимости, выпрямление экспоненциального спада, приближение к прямому спаду.
Таким образом, в результате мы пришли к выводу, что при анализе зависимости ТППФР от величины интервала ожидания следует осуществлять следующие операции с данными: 1- упорядочение величин времени реакции и времен ожидания, 2- фиксация значений времени реакции в диапазоне больших величин ожидания в точке нового увеличения снижения кривой (повышения 1-й производной спада), 3- сглаживания зависимости для уменьшения ступенек в спаде, 4- использование модели ТППФР как многокомпонентного экспоненциального спада с постоянной составляющей.
Величина ошибки R2, равная 519,3, дает среднеквадратичное отклонение ![]()
![]()
![]() = 3,2, что по сравнению с изменениями времени реакции (150-600) достаточно небольшая величина. В результате мы можем говорить, что предлагаемый подход позволяет проводить различные сравнительные исследования достаточно нового явления, ТППФР, поскольку выясняется, что у этого явления есть достаточно сложная структура.
= 3,2, что по сравнению с изменениями времени реакции (150-600) достаточно небольшая величина. В результате мы можем говорить, что предлагаемый подход позволяет проводить различные сравнительные исследования достаточно нового явления, ТППФР, поскольку выясняется, что у этого явления есть достаточно сложная структура.
Библиографический список
- Кулаков А.А. Лабораторная работа «Определение простой психомоторной реакции» //сборник материалов XIV Всероссийская конференция школа «Химия и инженерная экология» 27 июня 2014 с.70.
- А.Л. Сальманов, Д.В Ежов, А.А. Кулаков, Программа определения простой и дифференцированной психомоторной реакции на раздражитель // ХХ Туполевские чтения, Межд. Молодеж. Конф.,2012, т.3, ч.1. с.232-233
- Кулаков А.А. Влияние предварительного реагирования на скорость простой психомоторной реакции. / Материалы VII Межд. научно-практ.конф. «Актуальные направления фундаментальных и прикладных исследований» 19-20 октября2015 г. North Charleston, USA Том 3, с.8-10
- Уточкин И.С., Феликман М.В. Торможение возврата внимания. Часть 1. Виды и свойства. / Психологический журнал, 2006, т. 27, №3, с. 42-48
- Кулаков А.А. Анализ зашумленного экспоненциального спада как моделирование торможения простой психофизиологической реакции / III международной научно-практической конференции «Современные проблемы развития фундаментальных и прикладных наук».v. 3, Прага, 2016, c. 67-75
- Кукинов А.М. Применение порядковых статистик и ранговых критериев для обработки наблюдений. / В. кн: Поиск зависимости и оценка погрешности., М. Наука., 1985, с. 97-110
- Дьяконов В.П. Справочник по алгоритмам на языке бейсик для персональных ЭВМ. М., Неука, 1987, 240 с.
Количество просмотров публикации: Please wait


