Динамические системы со сложной и хаотической динамикой в настоящее время вызывают значительный интерес у исследователей и инженеров, специализирующихся в различных областях науки и техники. При этом результаты фундаментальных и прикладных исследований подобных динамических систем являются основой для разработки современных высокоэффективных радиоэлектронных устройств как гражданского, так и военного назначения. Среди основных областей науки и техники, в которых применение подобных устройств способно обеспечить существенное преимущество по сравнению с традиционно используемыми технологиями, необходимо отметить создание систем позиционирования, локальной навигации и радиолокации повышенной точности гражданского и военного назначения, высокозащищённых систем связи и передачи информации, медицинские системы неинвазивной диагностики различных заболеваний, системы шифрования данных, генераторы случайных чисел, устройства преобразования сигналов различного назначения и т.д.

Очевидно, что популярность детерминированного хаоса в области прикладных и фундаментальных исследований в дальнейшем будет только возрастать, однако для оптимизации процесса разработки источников хаотических колебаний с требуемыми характеристиками необходим простой и точный инструмент для моделирования устройств со сложной динамикой на стадии их разработки. В противном случае процесс разработки сведётся к методу последовательных приближений – изготовлению нового экспериментального макета путём исследования и корректировки предыдущего. Однако неизвестно приведёт ли данный метод к какому-либо положительному результату, особенно при разработке СВЧ-генераторов хаоса [1, с. 105]. В любом случае данный метод требует существенных временных и материальных затрат. Таким образом, до этапа макетирования целесообразно провести моделирование будущего генератора хаотических колебаний. В низкочастотной области с моделированием подобных схем проблем не возникает: существует множество простых моделей нелинейных элементов, в том числе биполярных и полевых транзисторов [2, с.1 , 3, с. 867], предоставляемых разработчиками и включенных в широко распространённые системы автоматизированного проектирования (САПР). Однако с переходом в диапазон сверхвысоких частот необходимо кроме основных характеристик компонентов учитывать, их паразитные параметры, а также инерционность обратной связи, и распределённый характер составляющих импеданса активного элемента [1, с. 121, 4, с. 42]. Задача моделирования генератора хаоса на основе СВЧ-диодов осложняется тем, что доступных моделей подобных активных элементов, которая может быть использована при моделировании генератора хаоса в САПР, на данный момент нет.

В то же время доступен другой метод моделирования, состоящий в анализе системы уравнений, составленной на основе принципиальной или эквивалентной схемы [1, с. 203, 5, с. 421, 6, с. 4]. При этом существует возможность учесть основные паразитные параметры и эффекты [7, с. 491, 8, с. 330, 9, с. 53]. Для моделирования динамических систем со сложной и хаотической динамикой, аналитические методы решения дифференциальных уравнений либо полностью неприменимы, либо их использование сопряжено с существенными трудностями, по этой причине для получения практически обозримых результатов используются численные методы решения [10, с. 2, 11, с. 110, 12, с. 128, 13, с. 19].

Однако, применение численных методов для решения систем дифференциальных уравнений, обладающих сложной нерегулярной динамикой, может привести к некорректным результатам [11, с. 112]. Исследуемая система может иметь регулярный, но более сложный аттрактор, витки которого близко расположены, что может приводить к перескокам численной траектории в пределах аттрактора вследствие ошибок в вычислениях, связанных с некорректностью решаемой задачи.  Для проверки достоверности полученного численного решения, необходимо проводить сравнение результатов, полученных при разных шагах интегрирования (при разных величинах допуска ошибки) [11, с. 112]. Если при разных шагах интегрирования полученное численное решение обладает свойствами хаотичности, то можно сделать вывод, что причиной хаотичности решения являются свойства самой динамической системы, а не ошибки численного решения.

В большинстве научных источников система дифференциальных уравнений, описывающая исследуемую нелинейную систему, решаются методом Рунге-Кутта 4-го порядка [1, с. 53, 12, с. 132, 14, с. 95], однако, в большом количестве работ, посвященных исследованию систем со сложной и хаотической динамикой, метод решения системы дифференциальных уравнений не указан. При этом какое-либо обоснование выбора того или иного метода численного решения систем дифференциальных уравнений полностью отсутствует. Упоминание о точности полученного численного решения при анализе систем со сложной и хаотической динамикой, либо хотя бы грубая его оценка также встречается в научной периодической печати крайне редко, хотя численному исследованию динамических систем с хаотической динамикой посвящено достаточно большое количество работ как в России, так и за рубежом. При этом возникает вопрос, имеющий важное практическое значение: насколько точен и эффективен тот или иной метод численного решения систем дифференциальных уравнений, описывающих динамическую систему со сложной или хаотической динамикой.

При этом анализ точности численного решения различными методами следует проводить на специальной тестовой задаче, к которой в данном случае предъявляются особенные требования, главное из которых состоит в том, что при изменении управляющих параметров системы в ней должны наблюдаться различные динамические режимы, в том числе режим динамического хаоса.

Одними из наиболее распространенных активных элементов, на основе которых возможна практическая реализация генераторов хаотических колебаний СВЧ- и ММ-диапазона, являются диод Ганна и лавинно-пролётный диод. Что делает целесообразным разработку тестовой системы на основе эквивалентной схемы, включающей указанные активные элементы. Динамические системы на основе указанных активных элементов относятся к классу регенеративных систем, поэтому подобная тестовая система будет описывать не только реальные радиотехнические устройства, в том числе СВЧ-диапазона, включающие лавинно-пролётные диоды или диоды Ганна, но также и все устройства, относящиеся к классу регенеративных системы.

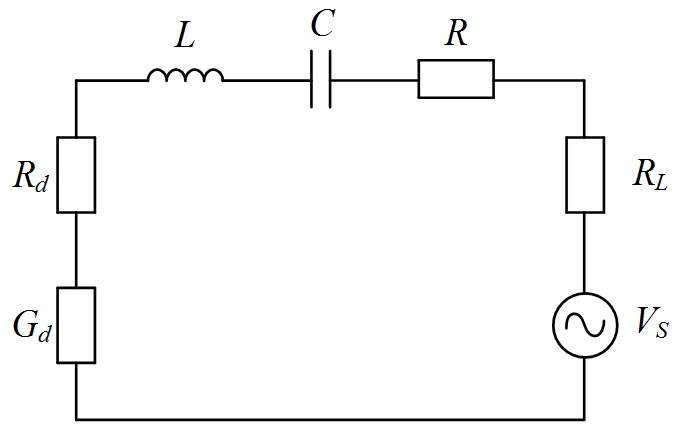
На рис.1 представлена теоретическая модель генератора на диоде Ганна по переменному току.

Рис.1. Эквивалентная схема СВЧ-генератора на диоде Ганна

На рис. 1 использованы следующие обозначения: R, L, C – эквивалентные значения сопротивления потерь, индуктивности и ёмкости резонатора; источник напряжения V_S представляет собой поле внешнего источника в резонаторе; R_d и G_d – активная и реактивная составляющие импеданса активного элемента; R_l – сопротивление нагрузки.

Дифференциальное уравнение, составленное на основе эквивалентной схемы СВЧ-генератора на диоде Ганна и описывающее динамику системы в различных режимах работы, после незначительных логически очевидных преобразований и нормализации имеет следующий вид [15, с. 327]:

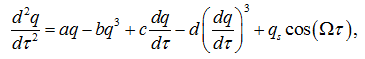       (1)

где dq/dt = i – мгновенное значение тока, τ = ω_rt – нормализованное время, ω_r=(LC)^-1/2 – резонансная частота колебательного контура, q_s и Ω – заряд, эквивалентный амплитуде и нормализованная угловая частота поля внешнего источника, присутствующего в резонаторе. Коэффициенты a, b, c, d – связаны с активной и реактивной частями импеданса диода Ганна и резонатора следующим образом:

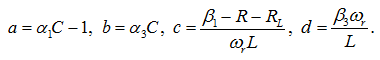
Очевидно, что коэффициенты a, b, c, d сложным образом зависят от величины напряжения смещения через параметры β₁, β₃, α₁ и α₃. Так как α₁ и α₃ связаны с параметрами эквивалентной емкости, то их значения определяются резонансной частотой. Параметры β₁ и β₃ связаны с эквивалентным сопротивлением диода Ганна, поэтому они играют большую роль в анализе возникновения колебаний. Кроме того, значение параметра β₃ много меньше по сравнению с величиной β₁, поэтому параметр d принимает значения меньшие величины параметра c [15, с. 328].

Необходимо отметить, что получить решение уравнения (1) весьма затруднительно [15, с. 328], поэтому для упрощения дифференциального уравнения целесообразно ввести новую переменную p = dq/dt. В результате подобного преобразования уравнение примет следующий вид:

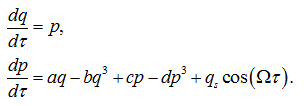    (2)

Традиционно для тестирования численных методов решения дифференциальных уравнений используются тестовые задачи, точное аналитическое решение которых известно, что позволяет сравнить полученное численное решение с точным как для качественного анализа, так и для количественной оценки погрешности численного решения [16,с. 3]. Однако, точное аналитическое решение возможно только в гармоническом режиме работы исследуемой динамической системы. В случае исследования динамической системы в режиме работы, отличном от гармонического, особенно в режим динамического хаоса, получить точное аналитическое решение невозможно. В лучшем случае можно говорить о приближенной оценке решения [17, с. 2], которое получено путём тех или иных упрощений и допущений в постановке задачи, что не позволяет использовать его в качестве точного решения при оценке численных методов. Таким образом, требование наличия точного аналитического решения тестовой задачи в рассматриваемом случае теряет свою актуальность. В данной ситуации необходимо использовать иные способы оценки точности численного решения.

Таким образом, составленное дифференциальное уравнение (2) описывает динамику широкого спектра динамических систем, относящихся к классу регенеративных систем, в том числе СВЧ-генераторов на основе лавинно-пролётных диодов и диодов Ганна в различных режимах работы, в том числе режиме динамического хаоса [18, с. 41]. Поэтому его целесообразно использовать в качестве тестовой задачи для оценки точности и эффективности численных методов решения систем дифференциальных уравнений, описывающих системы с сложной и хаотической динамикой. Преимущество использования данного уравнения в качестве тестового, кроме того, что оно описывает динамику широкого спектра реальных систем и устройств, состоит в том, что в зависимости от заданного набора значений параметров, возможно получить различные динамические режимы, в том числе автоколебательный режим, многочастотный режим и режим динамического хаоса.

Источники финансирования и выражение признательности

Исследование выполнено при финансовой поддержке Российского Фонда Фундаментальных Исследований в рамках научного проекта № 16-07-00631 а.

1. Генерация хаоса. Под общ. ред. Дмитриева А.С.-М: Техносфера, 2012.-424 с.
2. Бирюков В.Н., Пилипенко А.М., Семерник И.В. Таблично-аналитическая модель полевого транзистора для криогенных температур [Электронный ресурс] // Инженерный вестник Дона, 2012.-№4, Ч. 2.-Режим доступа: http://ivdon.ru/magazine/archive/n4p2y2012/1402(доступ свободный).
3. Бирюков В.Н., Пилипенко А.М., Семерник И.В., Шеховцова И.В. Диагностика дифференциальных параметров моделей полевых транзисторов // Радиотехника и электроника.-2015.-т.60, №8.-С. 865-872.
4. Дмитриев А.С., Панас А.И. Динамический хаос: Новые носители информации для систем связи.-М.: Физматлит, 2002.-252 с.
5. Atsushi Uchida. Optical communications with chaotic lasers. Applications of nonlinear dynamics and synchronization.-Wiley-VCH,2012.-630p.
6. Рыскин Н.М., Шигаев А.М. Сложная динамика простой модели распределённой автоколебательной системы с запаздыванием // Журнал технической физики.-2002.-т.72.-№7.-С. 1-8.
7. Семерник И.В., Алексеев Ю.И., Демьяненко А.В. Модель для анализа динамики развития хаотических колебаний в генераторе на лавинно-пролётном диоде при наличии неоднородности в выходной линии передачи // Материалы VII Международной  научной конференции «Излучение и рассеяние электромагнитных волн («ИРЭМВ-2013»)».-Таганрог: Изд-во ЮФУ, 2013.-С. 489-493.
8. Семерник И.В., Алексеев Ю.И., Демьяненко А.В. Модель для теоретического анализа режимов работы генератора на лавинно-пролётном диоде с учётом собственного отражённого сигнала // Известия высших учебных заведений. Физика.-2013.-т.56, № 8/2.-С. 329-331.
9. Алексеев Ю.И., Демьяненко А.В., Семерник И.В. Исследование хаотических состояний автоколебательных систем. Генератор на лавинно-пролетном диоде. Монография.-Saarbrücken, Deutschland.: LAP LAMBERT Academic Publishing GmbH&Co.KG, 2013.-133 c. ISBN-13: 978-3-659-49178-8.
10. Рыскин Н.М., Шигаев А.М. Сложная динамика простой модели распределённой автоколебательной системы с запаздыванием // Журнал технической физики.-2002.-т.72.-№7.-С. 1-8.
11. Магницкий Н.А. Теория динамического хаоса.-М.: ЛЕНАНД, 2011.-320 с.
12. Максимов Н.А., Панас А.И., Савельев С.В. Генерация хаотических колебаний в системе связанных однотранзисторных генераторов СВЧ диапазона // 14th Int. Crimean conference “Microwave & Telecommunication Technology” (CriMiCo’2004).-2004.-pp. 128-129.
13. Семерник И.В., Алексеев Ю.И., Демьяненко А.В. Точность решений, получаемых при численном анализе автоколебательных СВЧ-систем в состоянии детерминированного хаоса // Нелинейный мир.-2014.-т.12, №1.-С. 18-24.
14. Анищенко В.С. Сложные колебания в простых системах: Механизмы возникновения, структура и свойства динамического хаоса в радиофизических системах.-М.: Книжный дом «ЛИБРОКОМ», 2009.-320 с.
15. Sarkar B.C., Koley C., Guin A.K., Sarkar S. Some numerical and experimental observations on the growth of oscillations in an X-band Gunn oscillator // Progress in electromagnetic research B.-2012.-Vol.40.-pp. 325-341.
16. Пилипенко А.М., Бирюков В.Н. Исследование эффективности современных численных методов при анализе автоколебательных цепей//Журнал радиоэлектроники,2013, № 9, С.1-11.
17. I.V. Semernik, A.V. Demyanenko. Analysis of Possibility of Application the Analytical Method for Solving Differential Equations Describing the Nonlinear System with Complex Dynamics. International Siberian Conference on Control and Communications (SIBCON), 12-14 May 2016.
18. Алексеев Ю.И., Семерник И.В., Демьяненко А.В. Динамика хаотического состояния генератора СВЧ на лавинно-пролетном диоде // Нелинейный мир, 2014, т.12, №3, С. 40-44.

Все статьи автора «Семерник Иван Владимирович»