Квантовые компьютеры способны разрушить большую часть, если не абсолютно все традиционные криптосистемы, которые широко используются в практике. Конкретно, системы, основанные на задаче факторизации целых чисел (например, RSA). Некоторые криптосистемы, как система RSA с четырех тысячными битными ключами, считаются полезными для защиты классических больших компьютеров от атак, но, вероятно являются абсолютно бесполезными против атак на большие квантовые компьютеры.

Одной из альтернатив пост-квантовых систем являются системы, основанные на решетках (lattice based). Данные системы известны высоким уровнем безопастности, основанной на «наихудших случаях» (worst-case hardness). Они основаны на сложности проблем решеток, основной из которых является проблема кратчайшего вектора (SVP).

На самом деле, мы рассматриваем приближенный вариант, когда мы находим вектор решетки, длина которого в α(n) раз больше кратчайшего ненулевого вектора. α(n) -коефициент апроксимация, n- размер решетки. Самый известный алгоритм проблем решеток – это LLL algorithm. [1]

Данный алгоритм протекает в полиномиальное время с коэффициентом аппроксимации 2^O(n).

В 1987 году Шнор расширил LLL алгоритм и этим улучшил коэффициент аппроксимации, но при этом увеличил время исполнения алгоритма [2]. Шнор заменил ядро алгоритма LLL, блоками большего размера.

Были предложены стойкие к колизиям хеш функции, основанные на решетках. Аджтай (Ajtai) предложил семейство односторонних функций [3], безопасность которых основана на наихудшем случае, SVP с коэффициентом аппроксимации n^c, где n – константа. Позже Гольдреих (Goldreich) показал, что данные функции стойки к колизиям. Для построения данного семейства хеш функций используются параметры, целые числа: n, m, q и d.

Выбор параметра n определяет безопастность хеш функции. Ключ к хеш функции задается матрицей M, выбранной равномерно из Z_q^n×m. Хеш функция

f_M : {0, . . . , d−1}^m → Z_qⁿ. Функция сопоставляет mlogd битам  nlogq бит,  для компрессии ввода, m >  log q/ log d. Данную хеш функцию очень легко реализовать, т.к. мы используем только сложение и умножение по модулю q, размер которого O(log n). Но нужно отметить проблему эффективности этих функций, размер их ключа растет квадратично в n, поэтому данные функции являются неэффективными. Из-за атак на данные функции комбинаторным методом [4,5], для получения безопасности 100 бит, нужно использовать ключ размером 500000 бит.

Чтобы увеличить эффективность, можно заменить матрицу M блоковой матрицей, каждый блок которой является циркулянтной матрицей:

M = [M⁽¹⁾ | . . . | M^(m/n)].

Данная структура блока уменьшает размер, нужный для хранения ключа, с nm до m элементов и также уменьшает время исполнения алгоритма, нужное для вычисления произведения матрицы на вектор My mod q.

Изменение структуры матрицы  привело к нахождению коллизии. При умножении каждого блока на постоянный вектор v_i *1 = (v_i, . . . , v_i), вывод функции f_Mтоже будет постоянным вектором  c * 1. Т.к. c может принимать q разных значений, то коллизия может быть найдена за полиномиальное время q или даже O(√q).  Данная проблема была решена с помощью Peikert-а и Rosen-а и с помощью Lyubashevsky и Micciancio, используя идеальные матрицы.

Для построения данного семейства хеш  функций используются параметры, целые числа: n, m, q, d и вектор f ∈ Z_n. В качестве ключа берется m/n векторов a₁, . . . ,a_m/n выбранных равномерно из Zⁿ_q . Хеширование происходит следующим образом:

f_M : {0, . . . , d − 1}^m → Z_qⁿ , где  f_M (y) = [F∗a₁ | . . . | F∗a_m/n]y mod q.

В качестве M берется блочная матрица с структурированными блоками M⁽ⁱ⁾ = F∗a⁽ⁱ⁾ .

Для безопасности, основанной на «наихудших случаях», ветор f должен удовлетворять следующим условиям:

1. для двух единичных векторов u₁, u₂ вектор [F∗ u₁] u₂ должен иметь маленькую норму
2. Многочлен f(x) = xⁿ + f_nxⁿ⁻¹ + · · · + f₁ ∈ Z[x] должен быть не сократим на целые числа

В [6] были предложены значания ветора f, удовлетворяющие обоим условиям:

f = (1, . . . , 1) ∈ Z_n, где n + 1 простое число
f = (1, 0, . . . , 0) ∈ Zn, где n степень двойки.

Семейство хеш функций SWIFFT представляет оптимизированный вариант хеш функции, описанной выше, и является довольно эффективным благодаря использованию  FFT в Z_q. Вектор f = (1, 0, . . . , 0) ∈ Zn, где n степень двойки.

Для построения данного семейства хеш функций используются параметры, целые числа: n, m, d и параметр q – простое число, такое, что 2n делит q-1.

В качестве ключа берется m/n векторов b₁, . . . ,b_m/n выбранных равномерно из Zⁿ_q .

Принимаются m/n векторов : y₁,  . . . , y_m/n ∈ {0, . . . , d − 1}ⁿ

На выходе мы получаем вектор: ∑_i=1^m/nb⁽ⁱ⁾ ◦ Wy⁽ⁱ⁾ ∈ Z_n ^q; ◦ – покомпонентное векторное произведение. W ∈ Z^n×n_q, обратимая матрица в Z_q.

Функция хеширования переводит ключ и ввод функции в W*f_M(y) mod q,

где M = F∗a₁ | . . . | F∗a_m/n]; a⁽ⁱ⁾= W^-1 b⁽ⁱ⁾

Мультипликативная группа целых чисел по модулю q, Z_q^* имеет элемент w порядка 2n. За W возьмем матрицу Вандермонда (Vandermonde) с элементами:

w, w³,w⁵, … , w^2n-1; W = [w^(2i-1)(j-1)]^n,n _i=1,j=1.

Для избежания атак комбинаторным методом и атак, основанных на решетках, рекомендуются следующие параметры: n= 64; q= 257; m= 254; d= 2; w= 42; размер ключа – 8192 бит; размер ввода – 1024 бит ; размер вывода – 513 бит.

Были предложены схемы шифрования с открытым ключом, основанные на решетках. Голдреих, Голдвассер и Халеви предложили криптосистему: GGH, являющуюся аналогом криптосистемы McEliece, основанной на теории алгебраического кодирования [7].

Закрытым ключом является секретная матрица S, чьи столбцы формируют базис решетки L, данный базис состоит из коротких, почти ортогональных векторов.

Открытым ключом является открытая матрица B, формирующая плохой базис той же матрицы. Микианчио (Micciancio) предложил использовать  HNF (Hermite Normal Form) матрицы S.

Для шифрования сообщения, мы шифруем его как вектор m случайным образом, генерируем вектор ошибки v и высчитываем шифр: c = Bm + v

v сгенерировано из {-p,p}ⁿ. p- параметр безопасности.

Для расшифровки вычисляем: m = B⁻¹S[S^-1c].

В 1999 году, Nguyen опубликовал атаку на GGH,способную взломать систему для размеров матрицы до 350. Эта атака успешна из-за двух уязвимостей системы:

Первая заключается в том, что векторы ошибок всегда очень коротки по сравнению с векторами решетки. Это приводит к тому, что проблему CVP, т.е. проблему самого близкого вектора, становится легче решить.

Вторая уязвимость заключается в выборе вектора ошибки. Nguyen предложил несколько вариантов исправления второй уязвимости, но все они приводят к увеличению первой.

Из-за данной атаки приходится увеличивать размер матрицы, что делает систему неэффективной.

Также надо отметить, что данная система не является семантически безопасной.

В 1996 году Хофштейн, Пифер и Силверман предложили криптосистему NTRU.

NTRU обычно описывается как кольцевая криптосистема многочленов. Тем не менее, связь между открытым и закрытым ключами определяет решетку, которая называется решеткой NTRU. Базис для этой решетки может быть получен из открытого ключа. Кроме того, закрытый ключ криптосистемы соответствует определенным коротким векторам в этой решетке. Таким образом, естественная атака на эту систему – это попытка решить проблему кратчайшего вектора в данной решетке. Тем не менее, не обязательно использовать решетки во время шифрования и дешифрования.

Закрытым ключом является короткий вектор (f , g) ∈ Z²ⁿ. Открытый ключ –  h = p[R*f ]^-1g mod q, где p – это маленький модуль, R это циклический поворот, переводящий вектор  (x₁, x₂, … , x_n)^T в (x_n, x₁, … , x_n-1)^T, p – это большой модуль.

Шифрование происходит следующим образом: сообщение шифруется как вектор m ∈ {1,0,-1}ⁿ, для случайности используется вектор r ∈ {1,0,-1}ⁿ, содержащий

d_r записей -1, а всех остальных – 0. d_r –граница целого числа для r.

Шифр высчитывается: c = m + [R∗h]r mod q

Для расшифровки:

red = [R*f ]c (mod q);  все коеффиценты red должны лежать в интервале: [-q/2;q/2].

Сообщение высчитываем: m = [R*f ]_p^-1red (mod p);

Коперсмит и Шамир (Coppersmith, Shamir) осуществили атаку на закрытый ключ системы. Целью атаки является обнаружить векторы f и g или векторы, близкие к ним, которые можно использовать для расшивровки шифра. Вектор (f, g) и его попарные вращения представляют собой векторы в решетке NTRU. Евклидова норма этого вектора равна (2d_f − 1 + 2d_g)^1/2. Объем решетки NTRU задается как Det (L) = qⁿ и размерность решетки 2n. Ожидается, что кратчайший вектор имеет длину приблизительно det(L) ^1/2n = q^1/2

Т.к. (2d_f − 1 + 2d_g)^1/2<< q^1/2, с большой вероятностью вектор (f, g) является кратчайшим вектором решетки, значит, его попарные вращения являются также кандидатами ны самый короткий вектор. Также эти векторы можно использовать для расшифровки шифра.

Коперсмит и Шамир показали, что в случае, если полученный вектор больше, чем (f, g) на какую-то постоянную величину, можно скомбинировать несколько таких векторов и этим расшифровать шифр.

При использовании современных алгоритмов сокращения решетки коеффициент апроксимации кратчайшей векторной задачи все равно экспоненциален в n.

Howgrave-Graham показал, что возможно улучшить эту атаку, если скомбинировать ее с комбинаторной атакой. Чтобы противостоять данной атаке, надо увеличить параметры системы.

Открытый ключ системы имеет размер n log₂(q) . Время выполнения алгоритма зависит от n и от  границ целых чисел. Для увеличения эффективности системы в роли закрытого ключа можно брать f= u+pf_r, где u – это первый единичный вектор, а записи f_rслучайно выбраны из (1, 0, −1) в зависимости от d_f. Этим мы увеличиваем эффективность, так как мы избавляемся от шага умножения.

Криптосистема NTRU является намного более эффективной чем GGH и AD.

AD криптосистема была предложена Ajtai-Dwork-ом в 1997 году. Данная система определяется в евклидовой настройке векторного пространства, используя стандартную евклидову норму. Параметр безопасности n определяет размерность векторного пространства.

Закрытый ключем выбираится вектор u случайным образом из шара B размера n, с радиусом n^-c, для целого c>0. На n размерном кубе C определено распеределение U следующим образом:

берется x из {x ∈ C:, <x,u> ∈ Z } случайным образом, рисуются n векторов ошибки e₁,e₂,…,e_nиз шара B тоже случайным образом. Выдается v = x + ∑ⁿ_i=1e_i.

Для выбора открытого ключа из U случайным образом берутся векторы w₁, w₂, … , w_n и  v₁,v₂, … , v_m. w_i должны бать выбраны таким образом, чтобы параллелепипед, который они образуют, не был бы очень плоским, если это не так, то генерируется новый ключ. Шифрование выполняется на один бит за один раз. Для шифрования бита 0 берутся

b₁,b₂, … , b_m  случайным образом из {0,1} и уменьшается на ∑_ib_iv_iпо модулю параллелепипед, который образуют w_i. Для шифрования бита 1 случайным образом выбирается n размерный вектор из параллелепипеда, и он используется как шифр.

Для расшифровки высчитывается внутреннее произведение векторов c и u. Если расстояние (<c,u>, Z) <= n^-1, тогда c расшифровывается как 0, в  другом случае как 1.

Нгюен и Штерн (Nguyen , Stern) показали возможную атаку на данную криптосистему. Они свели различия между нулем и единицей к аппроксимации SVP в пределах коэффициента n^0.5-eps или CVP в пределах коэффициента n^1.33. Как показали Голдреих и Голдваисер (Goldreich , Goldwasser), аппроксимация CVP с таким коэффициентом не является NP трудной.

Для расшифровки с CVP, Нгюен и Штерн строят решетку размерности n+m в R^2n+m_, которая включает такие w_iи v_i,что шифрование нулей находится близко от решетки.

Позже Нгюен и Штерн осуществили атаку на закрытый ключ системы с помощью построения решетки в R^n+m, зависящей только от v_iи потом с помощью приближения внутреннего произведения v_iи u, с помощью умного использования коротких векторов в решетке. При достаточном количестве этих приближений, секретный вектор u может быть в достаточной степени приближен для взлома системы.

Регев (Regev) предложил криптосистему LWE[8], данная криптосистема считается самой эффективной системой, основанной на решетках.

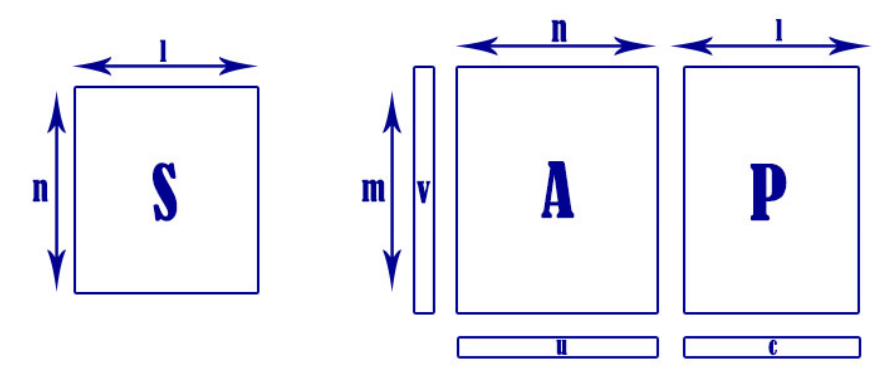
Закрытым ключом системы является матрица S ∈ Zq ^nxl, выбранная случайным образом. q,n и l целые числа.

Открытым ключом является (A,P = AS+E) ∈ Z_q ^mxn x Z_q ^mxl, где A ∈ Z_q ^mxn, выбранная случайным образом. E ∈ Z_q ^mxl, где данные выбираются согласно распределению Ψ_α, над Z_q, полученному путем выборки обычной переменной со средним значением 0 и отклонением αq/(2π)^1/2, округлением результата до ближайшего целого числа и уменьшением его по модулю q.

Шифрование происходит следующим образом: дается элемент из пространства сообщения e ∈ Z_t^l  и открытый ключ (A,P), выбирается вектор v ∈ {-d, -d+1, … , d}^m случайным образом, d – целое число, и выдается шифр: (u = A^Tv,c = P^Tv + f(e)) ∈ Z_qⁿ x Z_q^l. 

Расшифровка происходит следующим образом: Дается шифр (u,c) Z_qⁿ x Z_q^l и закрытый ключ: S ∈ Zq ^nxl и выдается: f^-1(C-S^Tu)

Рис. 1 Криптосистема LWE

Данную систему довольно легко реализовать, используя только сложение и умножение по модулю q. Для оптимизации времени выполнения можно t установить степенью двойки и если откладывать операции сокращения по модулю.

Данная система обладает следующими свойствами:

Размер открытого ключа:  nl log q

Размер закрытого ключа:  m(n+l) log q

Размер сообщения: l log t

Размер шифра: (n+l) log q

Фактор увеличения шифрования: (1+n/l)loq/logt

Операции, нужные для шифрования одного бита: O(m(1+n/l))

Операции, нужные для расшифровки одного бита: O(n)

Также были предложены системы электронной подписи, основанные на решетках.

Были предложены системы электронной подписи GGH и NTRUSign[9].

Закрытым ключом является секретная матрица S, чьи столбца формируют базис решетки L, данный базис состоит из коротких, почти ортогалнальных векторов.

Открытым ключом является открытая матрица B, формирующая плохой базис той же матрицы.  Лучше всего использовать  HNF (Hermite Normal Form) матрицы S.

Для шифрования сообщения мы отображаем его в точку m ∈ Rⁿ, используя секретный базис, затем мы округляем m до рядом находящейся точке n ∈ L(S), используя секретный базис. Это происходит с  помощью процедуры округления Бабая (Babai’s)

n = S[S^-1m].

Для верификации  пары подписи и сообщения (m,n) нужно проверить, что

n ∈ L(B) = L(S), используя открытый ключ B, и что расстояние от n до m маленькое.

 

Джентри и Шидло (Gentry ,Szydlo) заметили, что каждая подпись дает утечку информации о секретном ключе. Через несколько лет Нгюен и Регев (Nguyen, Regev) показали, что данная утечка ведет к атаке на сектретный ключ.

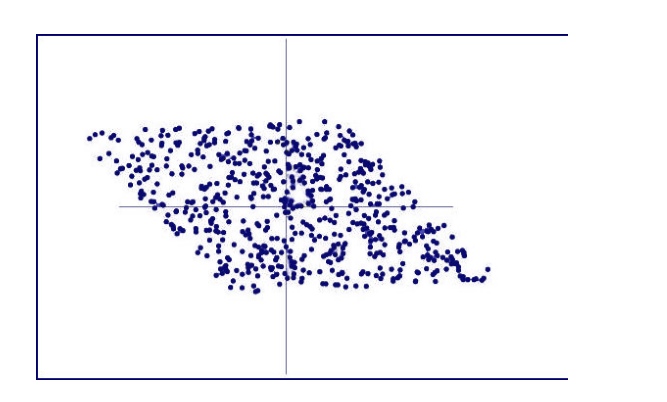
Основная идея атаки в том, что разница m-n распределена равномерно. Следовательно, учитывая достаточное количество таких пар, мы в конечном итоге приходим к алгоритмической проблеме – так называемой скрытой проблеме параллелепипеда (рис 2).

Рис 2. Скрытая проблема параллелепипеда

Решение данной проблемы приводит к данной атаке. Для защиты от данных атак наиболее эффективными мерами являются методы искажения. Скрытый параллелепипед заменяется более сложными фигурами, что помогает предотвратить данные атаки. Данные методы защиты замедляют генерацию подписи и увеличивают размер закрытого ключа.

Джентри, Пейкерт и Вайкунтанатан (Gentry, Peikert, Vaikuntanathan) определили схему под названием «preimage sampleable trapdoor functions» и показали как построить ее на основе «наихудших случаев» проблем решетки. Данная конструкция может быть использоваться как вариант GGH с доказательством безопасности. Также данная схема не дает утечек информации о секретном базисе. Это достигнуто с помощью замены процедуры округления Бабая, процедурой отбора Гаусса. Система имеет квадратичную сложность, как в случае размера ключа, так в случае времени верификации.

Любашевский и Микианчио предложили схему электронной подписи (Lyubashevsky, Micciancio) с безопастностью, основанной на «наихудших случаях» проблем решетки, схема является асимптотически эффективной, как в случае размера ключа, так в случае времени верификации имеет линейную сложность[10]. Данная система использует новую одноразовую систему подписи, основанную на хешировании. Такого типа схемы могут быть преобразованы в полноценные схемы подписи с использованием стандартных конструкций дерева только с логаритмической потерей эффективности. Одноразовая схема подписи основана на хеш функции, резистентной к колизиям, основанной на идеальных решетках. Хэш-функция h, может быть выбрана в процессе генерации ключа, или быть фиксированным параметром. Вводимые данные функции -это векторы v₁, … v_m/n∈Zqⁿ. Закрытым ключем функции является случайно выбранная пара x₁, … x_m/n∈Zqⁿи v₁, … v_m/n∈Zqⁿ, выбранная в соответствии с соответствующим распределением, которое генерирует короткие векторы с высокой вероятностью. Открытым ключом является образ данных двух значений ввода: X = h (x₁, … x_m/n) и V= h (v₁, … v_m/n). Сообщения представлены в виде коротких векторов: m ∈Zqⁿ. Подпись высчитывается так:

sig = (sig₁, … x_m/n) = ([F*m]x_{1 +} v₁, … [F*m]x_{m/n +} v_m/n) mod q.

Для верификации подписи проверяется, является ли sig последовательностью коротких векторов, которая хешируется в [F*m]X + V mod q.

Безопасность схемы опирается на то, что даже после того, как злоумышленник увидит подпись, значение секретного ключа скрыто от него.

Как мы видим, несмотря на то, что предложены криптосистемы для пост-квантовой эпохи, основанные на решетках, на них фиксируются атаки и они являются не эффективными. Таким образом для создания и реализации безопасных и эффективных пост-квантовых криптосистем, основанных на решетках, необходимо провести довольно большую работу.

РАБОТА ВЫПОЛНЕНА В РАМКАХ НАУЧНОГО ГРАНТА «НАЦИОНАЛЬНОГО НАУЧНОГО ФОНДА  ШОТА РУСТАВЕЛИ» [№ YS15_2.1.2_9].

Библиографический список

1. Lenstra, A.K., Lenstra, Jr., H.W., and Lovász, L.: Factoring polynomials with rational coefficients. Math. Ann., 261(4):515–534 (1982).
2. Schnorr, C.P.: A hierarchy of polynomial time lattice basis reduction algorithms. Theoretical Computer Science, 53(2-3):201–224 (1987).
3. Ajtai, M.: Generating hard instances of lattice problems. In Complexity of computations and proofs, volume 13 of Quad. Mat., pages 1–32. Dept. Math., Seconda Univ. Napoli, Caserta (2004). Preliminary version in STOC 1996.
4. Wagner, D.: A generalized birthday problem. In Advances in cryptology (CRYPTO), volume 2442 of LNCS, pages 288–303. Springer (2002).
5. Blum, A., Kalai, A., and Wasserman, H.: Noise-tolerant learning, the parity problem, and the statistical query model. Journal of the ACM, 50(4):506–519 (2003). Preliminary version in STOC’00.
6. Lyubashevsky, V. and Micciancio, D.: Generalized compact knapsacks are collision resistant. In 33rd International Colloquium on Automata, Languages and Programming (ICALP) (2006).
7. Гагнидзе А.Г., Явич М.П., Иашвили Г.Ю. Пост-квантовые криптосистемы // Современные научные исследования и инновации. 2016. № 5 [Электронный ресурс]. URL: http://web.snauka.ru/issues/2016/05/67264
8. Regev, O.: Lattice-based cryptography. In Advances in cryptology (CRYPTO), pages 131–141 (2006).
9. Hoffstein, J., Graham, N.A.H., Pipher, J., Silverman, J.H., and Whyte, W.: NTRUSIGN: Digital signatures using the NTRU lattice. In Proc. of CT-RSA, volume 2612 of Lecture Notes in Comput. Sci., pages 122–140. Springer-Verlag  (2003).
10. Lyubashevsky, V. and Micciancio, D.: Asymptotically efficient lattice-based digital signatures. In Fifth Theory of Cryptography Conference (TCC), volume 4948
    of Lecture Notes in Computer Science. Springer (2008).

---

Количество просмотров публикации: Please wait

Все статьи автора «Явич Максим Павлович»