Введение. В понятие морфологической структуры насаждений входят вопросы пространственного распределения деревьев древостоя, подроста и подлеска, горизонтальной и вертикальной сомкнутости полога. В процессе измерительных работ могут изучаться также таксационно-дешифровочные показатели насаждений: диаметры и протяженности крон деревьев, высоты до наибольшего диаметра кроны, связи протяжения кроны с общей высотой или диаметра ствола на 1,3 м., зависимости между диаметрами крон и стволов на 1,3 м. и др. При изучении данных вопросов следует иметь в виду то, что ряд выводов по строению древостоев в тех или иных источниках нередко противоречив. Вызвано это игнорированием категорий объектов лесной таксации, недостаточной глубиной математического анализа или не полнотой исходного материала, отрывом развития леса от лесорастительных условий и др. [1]. В настоящее время нет специальной отрасли знаний – морфологии насаждений и, следовательно, нет научно обоснованных показателей, характеризующих внешний их облик [2]. В научной литературе приводятся отдельные данные по форме вертикальной и горизонтальной проекции крон, их изменениям и количеству в зависимости от возраста, полноты, возрастной структуры и других показателей [3]. Вопросы изучения горизонтальной и вертикальной структуры, сомкнутости крон и полога нашли отражение в работах А.А. Вайса [4-13]. Развитие данного вопроса важно не только с целью автоматизировании и упрощении дешифрирования, но и для лесоводственных исследований, так как все это позволит лучше узнать природу насаждений.
Цель исследования. Целью является изучение площади поверхности форм крон деревьев сосны, так как данный вопрос является неотъемлемой частью морфологической структуры насаждений. Исходя из этого, были поставлены следующие задачи:
- определение площади поверхности крон (вертикальная структура) и сравнение её с эталонной формой фотографии с учетом масштаба;
- определение площади поперечного сечения крон деревьев (горизонтальная структура) и сравнение её с эталонной формой фотографии с учетом масштаба;
- установление эмпирических формул для вычисления площади горизонтальной и вертикальной поверхностей проекций крон сосны в максимально полных насаждениях.
Объекты и методы исследований.
В качестве объектов исследования было выбрано насаждение с модальным таксационным составом и характеристиками (таблица 1).
Таблица 1- Таксационные характеристики объектов исследования

Номер	Состав	А,  лет	Н, м	D, см	Бонитет	Тип леса	Полнота	Запас на га, м3
1	10С	83	23	26	2	СЗЛРТ	1,1	360

Методика исследования соответствовала общепринятым подходам лесной таксации. В каждой ступени толщины от 8 см до 40 см было выбрано по три модельных дерева, а в 40 и 44 ступенях по два дерева. У каждого дерева с помощью мерного шеста был определен средний радиус и диаметр по сторонам света. К каждому модельному дереву приставлялся 3-х метровый шест и фотографировался. Так же замерялся радиус крон по сторонам света с помощью мерного шеста. 
В камеральных условиях определялся масштаб для каждой фотографии. Далее с фотографий на миллиметровку переносились кроны (видимая и ядровая часть крон). Для определения вертикальной структуры у каждой кроны через равное расстояние был сделан замер диаметра (таблица 2). У каждой кроны была посчитана площадь поверхности. 
Визуально определив форму крон и сравнив с замерами диаметров каждую крону можно отнести к той или иной фигуре. Примеры форм крон приведены на рисунках 1 и 2.

Рисунок 1. Форма крон 8-24 ступеней толщины

Рисунок 2 . Форма крон 28 -44 ступеней толщины

Визуально определив форму крону, было установлено, что до 24 ступени толщины крона деревьев соответствует правильной, стереометрической фигуре прямоугольнику, а после 24 ступени такой плоскостной фигуре как круг.
Для того чтобы выявить степень несоответствия определили площадь вертикальной поверхности с правильной стереометрической фигурой прямоугольником и сравнили значения с площадью, рассчитанной по фотографии (таблица 3). 

Площадь прямоугольника находили по формуле:

s=a*b , (1)
где s – площадь прямоугольника, м²;
a – длина, м;
b – ширина, м.

Площадь круга находиться по формуле:

S=  , (2)

где S- площадь круга, м²; 
R- радиус круга, м.

Таблица 3 – Сравнение площадей поверхностей вертикальной проекции крон деревьев сосны

Ступень толщины, см	Площадь поверхности крон (стереометрический способ), м2	Площадь поверхности крон (фотография),  м2	Ошибка,%
8	4,75	7,06	-67,3
8	8,18	7,69	+6,4
8	4,71	4,13	+14,0
12	15,68	9,42	+66,5
12	16,62	10,22	+62,6
12	8,31	8,83	-5,9
16	30,34	19,19	+58,1
16	10,26	10,62	-3,3
16	10,70	5,19	+106,2
20	13,78	19,74	-31,2
20	10,01	14,26	-29,8
20	22,32	23,77	-6,1
24	1,09	1,67	-34,6
24	32,13	37,89	-15,2
24	11,50	16,30	-29,4
28	12,42	28,64	-143,4
28	5,95	12,76	-146,67
28	20,58	28,23	-27,1
32	44,94	30,94	+45,2
32	31,85	35,41	-10,0
32	16,97	11,99	+41,6
36	39,95	34,77	+14,9
36	37,83	40,82	-7,3
36	20,45	37,71	-45,8
40	57,31	64,19	-10,7
40	36,96	46,58	-20,6
44	135,54	61,12	+121,8
44	56,29	76,31	-26,2

Диапазон ошибок площади поверхности крон определенных стереометрическим способом и площади поверхности крон установленных фотографическим способом варьировал от +121,8 до -146,67 %.
Для установления вида коррекционных формул и определения площадей поверхностей крон (вертикальная структура) на основе таблицы 3 были построены графики связи величины ошибок и диаметров деревьев (для диаметров до 24 см рисунок 3., деревья от 28 см и выше рисунок 4). Для каждой совокупности были получены формулы (3), (4). 

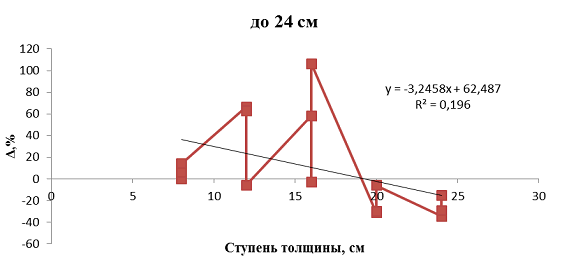
Рисунок 3. Связь погрешностей в определении площади крон с размерами деревьев по диаметру (до 24 см)

 

S=L*Dk*((-3*d_1,3+60)/100+1) , (3)

где S – площадь вертикальной проекции крон, м²;

L- длина кроны, м;

Dк – диаметр кроны, м;

d_1.3 - диаметр на высоте груди, см.

С увеличением диаметра кроны величина ошибки уменьшается.

S=П*R₂²*((7*d_1,3-250)/100+1) , (4)

где S- площадь вертикальной поверхности крон, м²;

П-3,14;

R – радиус круга, м;

d_1.3 - диаметр на высоте груди, см.

Величина ошибки после 28 ступени толщины с возрастанием диаметра увеличивается.

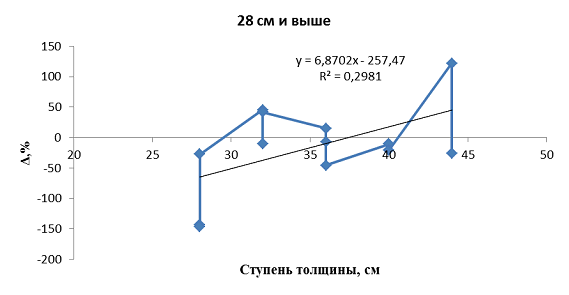
Рисунок 4. Связь погрешностей в определении площади крон с размерами деревьев по диаметру (28 см и выше)

Для того чтобы в дальнейшем перейти к определению объема кроны необходимо знать две составляющих, вертикальную и горизонтальную проекцию. Ранее было установлено, что горизонтальная проекция по средним значениям радиуса имеет форму круга [14], что позволяет представить крону как объемную фигуру.
У каждого дерева были сделаны замеры радиусов по сторонам света и рассчитаны ошибки (таблица 4). 

Таблица 4 – Площади горизонтальной проекции крон по сторонам света

Сту-пень тол-щи-ны, см	Пло-щадь пове-рхно-сти крон (сте-рео-метричес-кий спо-соб), м2	Пло-щадь поверх-ности крон (фото-гра-фия),  м2	Оши-бка (по С), %	Оши-бка (по В), %	Оши-бка (по Ю, %	Оши-бка  (по З), %	Оши-бка  (по С/Ю), %	Оши-бка (по В/З), %	Ошибка по сторо-нам света, %
8	1,23	1,22	-25,4	-25,4	36,0	7,8	7,8	-8,2	1,0
8	2,61	2,65	70,0	-20,1	-32,4	-45,3	27,9	-32,4	-1,1
8	3,30	3,10	65,7	-86,6	-60,9	39,1	14,1	-15,2	6,1
12	5,94	5,46	36,0	-19,0	-35,4	10,6	3,6	-3,7	8,8
12	3,46	3,17	-53,3	-30,6	9,3	55,6	-20,0	18,1	8,4
12	1,65	1,79	-130,2	6,8	52,4	31,5	-21,8	19,6	-7,8
16	13,20	5,14	39,1	14,1	-73,5	4,8	-10,0	9,5	6,7
16	4,71	5,71	-30,6	39,9	33,4	-60,1	4,0	-4,1	-17,5
16	5,51	13,02	-64,6	-105,6	18,0	85,8	-19,8	18,0	1,4
20	4,34	5,12	-283,2	47,7	53,6	59,3	-74,0	53,6	-15,2
20	5,00	5,11	-41,2	-81,3	54,7	37,3	13,4	-14,3	-2,0
20	9,07	6,63	83,0	-12,1	-191,0	32,2	-12,1	11,4	37,0
24	0,50	0,55	0,0	0,0	0,0	0,0	0,0	0,0	-9,1
24	15,37	14,44	-164,8	-77,8	68,1	77,5	-20,1	18,3	1,1
24	2,27	2,17	50,2	65,4	-300,0	50,2	-83,0	58,1	4,4
28	23,75	21,26	30,0	70,2	66,1	-314,7	49,7	-66,6	10,5
28	6,60	5,08	-246,7	69,6	85,6	-45,7	-25,6	22,7	29,9
28	12,40	11,42	35,2	-192,6	79,5	-6,4	60,4	-88,0	1,1
32	19,04	20,69	-58,5	20,2	5,0	23,8	-24,7	22,0	-0,9
32	27,33	28,92	22,3	9,9	-32,8	-3,4	-3,4	3,4	-0,9
32	10,46	10,59	23,1	-20,1	13,2	-20,1	18,3	-20,1	-1,0
36	50,24	50,69	23,4	-82,3	-62,6	75,0	-15,6	14,4	-0,9
36	26,18	23,79	6,0	2,6	69,3	-121,8	42,0	-53,3	11,0
36	16,97	15,03	22,3	-72,1	63,7	-45,0	45,0	-58,3	11,4
40	65,72	59,82	31,0	-44,5	3,3	3,3	17,7	-19,4	9,9
40	42,99	43,57	89,5	-171,8	-180,8	87,7	0,0	0,0	-1,3
44	59,42	61,15	-103,1	-16,7	81,9	-14,3	14,4	-15,5	-2,8
44	60,45	60,33	-48,7	25,0	50,1	-45,9	7,3	-7,5	0,2

Сведения таблицы 4 показывают, что с увеличением числа измерений величина погрешностей в большинстве случаев уменьшается. По данным ошибок четырех измерений был построен график (рисунок 5) и получено итоговое уравнение для определения площади поверхности:

S=П*Rcр²*((0,06*d_1,3+1,7)/100+1) , (5)

где S – площадь горизонтальной проекции крон, м²;

П-3,14;

R_ср - средний радиус, м;

d_1.3 - диаметр на высоте груди, см.

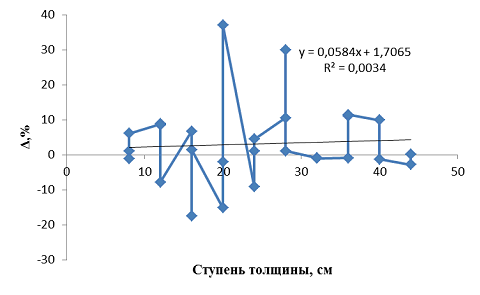
Рисунок 5. Связь погрешностей в определении площади горизонтальных проекций крон с размерами деревьев по диаметру

В результате проведенных исследований был предложен ряд эмпирических формул для вычисления площадей горизонтальной и вертикальной поверхностей проекций крон сосны в максимально полных насаждениях. При этом величина ошибок указывала на нецелесообразность использования стереометрического подхода для определения площади поверхности крон на данном участке. Для устранения ошибок необходимы более тщательные измерения, программные средства и т.д.

Библиографический список

1. Верхунов П.М. Изучение строения древостоев. Методические указания по дипломному проектированию. — Йошкар-Ола: Марийский политехнический институт имени М. Горького, 1981. — 45 с.
2. Самойлович  Г.Г. Применение аэрофотосъемки и авиации в лесном хозяйстве. Л.: 1972. 64 с.
3. Скоробогатько Н.Д. Строение дешифровочных показателей полога модальных еловых древостоев в равнинной части Прикамья и сосновых насаждений Курской области для автоматизированного дешифрирования аэрофотоснимков [Электронный ресурс]. Режим доступа: http://www.science-bsea.bgita.ru/2004/leskomp_2004/skorobogatko.htm/   Дата доступа 02.06.2016.
4. Вайс А.А. Научные основы оценки горизонтальной структуры древостоев для повышения их устойчивости и продуктивности (на примере насаждений Западной и Восточной Сибири): диссертация на соискание ученой степени доктора сельскохозяйственных наук, специальность 06.03.02. 2014. 418 с.
5. Вайс А.А. Научные основы оценки горизонтальной структуры древостоев для повышения их устойчивости и продуктивности: автореферат диссертации на соискание ученой степени доктора сельскохозяйственных наук, специальность 06.03.02. 2014. 33 с.
6. Вайс.А.А., Оскорбин П.А. Динамика пространственной структуры темнохвойных древостоев Западной Сибири//Известия высших учебных заведений:Лесной журнал.2009.№1.с.21-28.
7. Вайс А.А. Связь текущего прироста деревьев с морфологическими и социальными показателями на примере древостоев Восточной Сибири//Политехнический сетевой электронный журнал Кубанского государственного аграрного университета.2009.№ 47.с.113-129.
8. Вайс А.А. Исследование продуктивности сосняков таежной зоны на основе таксационно-дешифровочных признаков//Вестник Московского государственного университета леса-Лесной вестник.2005. № 6. с.18-22.
9. Вайс А.А. Моделирование толщины деревьев на основе сомкнутости полога биогруппы и морфологических признаков//Актуальные проблемы лесного комплекса. 2005. №12. с. 66-69.
10. Вайс А.А, Пчелинцев В.И. Динамика морфологических признаков соснового древостоя//Актуальные проблемы лесного комплекса.2004.№8. с.16-17.
11. Вайс А.А. Современные научные исследования в области таксации и лесоустройства//Исследования в области естественных наук. 2015.№3(39). с. 14-18
12. Вайс А.А. Аллометрические закономерности соотношения фитомассы хвои и диаметров древостоев в сосновых разнотравных древостоях Приангарского района//Международный журнал экспериментального образования. 2015. №11-2.с. 303-304.
13. Вайс А.А., Вараксин Г.С. Разряды защитной высоты в полезащитных насаждениях юга Средней Сибири//Лесная таксация и лесоустройство.2015.№1(52). с.22-26.
14. Ветошкина И.Н., Вайс А.А. Форма горизонтальной проекции крон деревьев сосны обыкновенной в условиях Идринско-Курагинского лесостепного округа Минусинской котловины // Современные научные исследования и инновации. 2016. № 1 [Электронный ресурс]. URL: http://web.snauka.ru/issues/2016/01/62475 (дата обращения: 24.05.2016).

---

Количество просмотров публикации: Please wait

Все статьи автора «Ветошкина Ирина Николаевна»