Абелевы группы без кручения ранга 2, представимые в виде подпрямой суммы абелевых групп без кручения ранга 1 образуют важный для изучения подкласс класса абелевых групп без кручения конечного ранга, а описание таких групп достаточно актуально в теории абелевых групп. В работах автора [1] – [4] ранее изучались группы из данного подкласса.
Определение 1. Пусть ![]() прямое произведение абелевых групп. Подгруппа G группы А называется подпрямой суммой групп Аi, если отображение
прямое произведение абелевых групп. Подгруппа G группы А называется подпрямой суммой групп Аi, если отображение ![]() для каждого номера i, где
для каждого номера i, где ![]() – проекция прямого произведения А на прямой сомножитель Аiявляется эпиморфизмом [5].
– проекция прямого произведения А на прямой сомножитель Аiявляется эпиморфизмом [5].
Группа G является подпрямой суммой групп А и В тогда и только тогда, когда существует группа F и такие эпиморфизмы ![]() и
и ![]() , что
, что ![]() для любых элементов
для любых элементов ![]() и
и ![]() [5].
[5].
Группу F назовем порождающей группой, а эпиморфизмы ![]() и
и ![]() – определяющими эпиморфизмами для группы G – подпрямой суммы групп А и В.
– определяющими эпиморфизмами для группы G – подпрямой суммы групп А и В.
Необходимые термины и обозначения приведены в работах [1-10].
Также будем использовать стандартные обозначения: ![]() – наибольший общий делитель целых чисел х и у,
– наибольший общий делитель целых чисел х и у, ![]() – соответственно, их наименьшее общее кратное.
– соответственно, их наименьшее общее кратное.
В данной статье продолжено изучение строения одного подкласса класса абелевых групп – так называемых специальных или s-групп (определение дается ниже) – в зависимости от основного элемента.
Далее, всюду в статье, если не сказано иначе, все группы абелевы, группы А и В – рациональные делимые, G – подпрямая сумма групп А и В, порождающую группу которой обозначаем через F, а также введем обозначения: ![]() и
и ![]() .
.
Символом ![]() обозначаем циклическую абелеву группу, порожденную элементом
обозначаем циклическую абелеву группу, порожденную элементом ![]() , символом
, символом ![]() множество всех подпрямых сумм групп А и B с порождающей группой
множество всех подпрямых сумм групп А и B с порождающей группой ![]() .
.
Определение 2. Абелева группа называется рациональной если она изоморфна группе Q рациональных чисел или ее подгруппе [5].
Определение 3. Абелева группа А называется делимой, если для любого натурального числа п: пА = А [5].
Пусть Т – некоторое числовое множество, х – некоторый элемент произвольной группы, тогда ![]() будем обозначать множество
будем обозначать множество ![]() .
.
Определение 4. Пусть группа ![]() ,
, ![]() ,
, ![]() . Будем говорить, что группа G обладает основным элементом
. Будем говорить, что группа G обладает основным элементом ![]() , если
, если ![]() ,
,![]() . Такую группу мы будем называть специальной или s-группой.
. Такую группу мы будем называть специальной или s-группой.
Пусть G – s-группа с основным элементом ![]() . Введем следующие обозначения:
. Введем следующие обозначения:
.gif)
где n – натуральное число ![]() , p простое число, т, т’ – целые числа, взаимно простые с числом р.
, p простое число, т, т’ – целые числа, взаимно простые с числом р.
Предложение 1. Для любого натурального числа п множество ![]() с операцией сложения является группой.
с операцией сложения является группой.
Доказательство. Пусть п – произвольное натуральное число. Покажем сначала, что ![]() (*) для любого целого числа k.
(*) для любого целого числа k.
Пусть ![]() . Условие (*) очевидно для взаимно простых чисел k и d, так как
. Условие (*) очевидно для взаимно простых чисел k и d, так как ![]() и, следовательно, по определению, принадлежит
и, следовательно, по определению, принадлежит ![]() .
.
Пусть ![]() , и пусть
, и пусть ![]() ,
, ![]() . Поскольку, очевидно,
. Поскольку, очевидно, ![]() , а также, как известно, числа
, а также, как известно, числа ![]() и
и ![]() взаимно просты, то получаем:
взаимно просты, то получаем:
.gif)
Далее рассмотрим два произвольных элемента

из множества ![]() и покажем, что их сумма также принадлежит
и покажем, что их сумма также принадлежит ![]() .
.
Пусть ![]() , причем
, причем ![]() ,
, ![]() . Тогда
. Тогда
.gif)
 ,
,
Поскольку, как нетрудно видеть, ![]() , то, следовательно,
, то, следовательно, ![]() . Откуда вытекает, что
. Откуда вытекает, что ![]() есть группа.
есть группа.
Докажем аналогичное утверждение для множества ![]() .
.
Предложение 2. Пусть G – s-группа. Для любого простого числа р множество ![]() образует группу подгруппу группы G.
образует группу подгруппу группы G.
Доказательство. Покажем также сначала, что произведение ru содержится в ![]() для любого целого числа r и любого элемента
для любого целого числа r и любого элемента ![]() .
.
Пусть для некоторых простого числа р и натурального числа i элемент .gif) . Тогда для взаимно простых чисел k и p, очевидно,
. Тогда для взаимно простых чисел k и p, очевидно, .gif) .
.
Пусть ![]() , где
, где ![]() , и пусть
, и пусть ![]() . Тогда
. Тогда
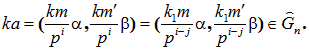
Установим теперь замкнутость множества ![]() относительно операции сложения. Рассмотрим два произвольных элемента
относительно операции сложения. Рассмотрим два произвольных элемента
.gif) и
и .gif)
из множества ![]() и покажем, что их сумма также принадлежит
и покажем, что их сумма также принадлежит ![]() .
.
Пусть ![]() . Тогда
. Тогда
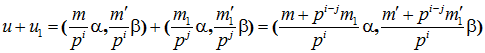 .
.
Поскольку, как нетрудно видеть,
то, следовательно, ![]() . Откуда вытекает, что
. Откуда вытекает, что ![]() есть группа.
есть группа.
Предложение 3. ![]() для любого натурального числа i и для любого простого числа p.
для любого натурального числа i и для любого простого числа p.
Доказательство непосредственно следует из определения множества ![]()
Определение 5. Пусть группы А и В изоморфны рациональной группе .gif) для некоторого простого числа р. И пусть для некоторой группы G* выполняются следующие условия:
для некоторого простого числа р. И пусть для некоторой группы G* выполняются следующие условия:
1) группа G* является подпрямой суммой групп А и В, с порождающей группой ![]() ;
;
2) группа G* обладает основным элементом.
Тогда группу G* будем называть р-специальной (или ps-группой).
Теорема 1. Пусть G – s-группа с основным элементом ![]() . Тогда, для любого простого числа р, выполняются условия:
. Тогда, для любого простого числа р, выполняются условия:
подгруппа ![]() группы G является рs-группой;
группы G является рs-группой;
группа ![]() может быть получена как объединение своих подгрупп, образующих бесконечную возрастающую цепь:
может быть получена как объединение своих подгрупп, образующих бесконечную возрастающую цепь:
где ![]() .
.
Доказательство. Рассмотрим группу ![]() для некоторого простого числа p. Тогда по определению,
для некоторого простого числа p. Тогда по определению, ![]() для некоторых рациональных групп
для некоторых рациональных групп ![]() и
и ![]() . Покажем, что группа
. Покажем, что группа ![]() образует подпрямую сумму групп
образует подпрямую сумму групп ![]() и
и ![]() , порожденную группой
, порожденную группой ![]() , с основным элементом
, с основным элементом ![]() .
.
Пусть элемент .gif) , причем числа т и рi взаимно просты. Тогда найдется такое целое число m‘ взаимно простое с числом рi, что элемент
, причем числа т и рi взаимно просты. Тогда найдется такое целое число m‘ взаимно простое с числом рi, что элемент .gif) принадлежит группе
принадлежит группе ![]() – подгруппе группы
– подгруппе группы ![]() . Но, по предложению 2 [5], если m” также целое число, причем числа m” и m‘ не сравнимы по модулю рi в кольце целых чисел, то элемент
. Но, по предложению 2 [5], если m” также целое число, причем числа m” и m‘ не сравнимы по модулю рi в кольце целых чисел, то элемент .gif) и, следовательно,
и, следовательно, ![]() .
.
Таким образом, доказано, что проекция ![]() является эпиморфизмом. Аналогично доказывается, что эпиморфизмом также является проекция
является эпиморфизмом. Аналогично доказывается, что эпиморфизмом также является проекция ![]() .
.
Следовательно, можем сделать вывод, что во-первых группа ![]() есть подпрямая сумма групп
есть подпрямая сумма групп ![]() и
и ![]() , а, во-вторых, порождающей группой является группа
, а, во-вторых, порождающей группой является группа ![]() .
.
Из определения групп ![]() и
и ![]() для каждого целого положительного числа i, непосредственно следует условие 2.
для каждого целого положительного числа i, непосредственно следует условие 2.
Теорема 2. Пусть G – s-группа с основным элементом ![]() и с порождающей группой
и с порождающей группой ![]() , и пусть элемент
, и пусть элемент ![]() , причем
, причем ![]() . Тогда существуют и причем, с точностью до нумерации, единственные простые числа р1, р2, …, рr такие, что
. Тогда существуют и причем, с точностью до нумерации, единственные простые числа р1, р2, …, рr такие, что
где
Д о к а з а т е л ь с т в о. Пусть п – целое положительное число, ![]() . И пусть для некоторых целых чисел k и т взаимно простых с числом п элемент
. И пусть для некоторых целых чисел k и т взаимно простых с числом п элемент ![]() . Тогда, очевидно, имеет место следующее равенство:
. Тогда, очевидно, имеет место следующее равенство:
где s, t, k’ и m’ – целые числа, причем k’ и m’ – наименьшие положительные, что ![]() ,
, ![]() . Кроме того,
. Кроме того, ![]() и
и ![]() (см. [4]), следовательно,
(см. [4]), следовательно, ![]() .
.
Пусть ![]() каноническое разложение числа п на простые множители. Как известно, такие простые числа р1, р2, …, рrсуществуют и единственны с точностью до нумерации. Нетрудно видеть, что найдутся целые числа х1, у1, х2, у2, …, хr, yr такие, что
каноническое разложение числа п на простые множители. Как известно, такие простые числа р1, р2, …, рrсуществуют и единственны с точностью до нумерации. Нетрудно видеть, что найдутся целые числа х1, у1, х2, у2, …, хr, yr такие, что
.gif) .
.Введя обозначения:
.gif) ,
, 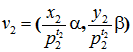 , …,
, …, .gif) ,
,а также ![]() , мы докажем требуемое утверждение.
, мы докажем требуемое утверждение.
Библиографический список
-
Трухманов В.Б. О некоторых свойствах подпрямой суммы бесконечных циклических абелевых групп //
Современные научные исследования и инновации. 2014. № 10-1 (42). С. 15-19. -
Трухманов В.Б. О подгруппах прямой суммы бесконечных циклических абелевых групп //
Исследования в области естественных наук. 2014. № 7 (31). С. 45-50. -
Трухманов В.Б. О некоторых специальных и р-специальных группах // Исследования в области естественных наук. 2014. № 6 (30). С. 5.
-
Трухманов В.Б. O подпрямой сумме делимых рациональных групп и ее основных элементах // Современные научные исследования и инновации. 2015. №4-1(48). С. 6-10.
-
Фукс Л. Бесконечные абелевы группы. Т.1. М.: Мир, 1974. 335 с.
-
Широков Л.В. Накрытия и их свойства // Современные научные исследования и инновации. 2014. № 9-1 (41). С. 5-11.
-
Широков Л.В. Класс пространств L и его свойства // Альманах современной науки и образования. 2014. № 8 (86). С. 181-183.
-
Широков Л.В. О некоторых свойствах d-регулярных отображений // Альманах современной науки и образования. 2014. № 9 (87). С. 152-155.
-
Широков Л.В. Современные проблемы радиоэлектроники с позиций теории конформных отображений / Ямпурин Н.П., Широков Л.В., Садков В.Д., Потехин В.А. Монография / Арзамасский филиал ННГУ, АПИ филиал НГТУ. Арзамас: Изд-во Арзамасского филиала ННГУ , 2014. 209 с.
-
Shirokov L.V. On some forms of embeddings of topological spaces // Russian Mathematical Surveys. 1987. Т. 42. № 2. С. 297-298.
Количество просмотров публикации: Please wait


