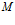Математическое прогнозирование – выявление событий, подтвержденными какими либо формулами, расчетами, образованными в единую и логическую цепочку и имеющими верные для расчета исходные данные.
Для произведения математического прогнозирования численности населения, по исходным данным за прошлые годы, мной было выбрано программное обеспечение CurveExpert1.4, так как в ней по исходным данным можно смоделировать график и найти функцию и ее переменные [1]. В данном случае формула будет иметь вид M=ƒ(t).
Составляющие формулы:
-
M – численность населения;
-
t- время, берем его от нуля до последнего по счету года.
Далее переходим непосредственно к самому программному обеспечению. В значения столбца X подставляем значения времени t, затем в столбец Y подставляем значение численности населения
M. Начинаем моделирование данных по исходным значениям таблицы 1.
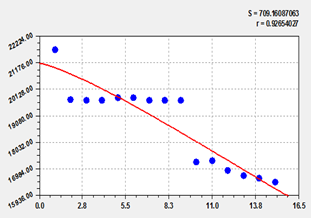
Результаты моделирования смотри на рисунке 1.
 |
 |
| а | б |
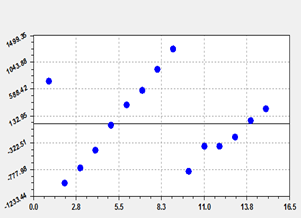
Рис.1 Результаты идентификации численности населения от года:
а – график модели; б – остатки от модели.
Произведя моделирование, выявили формулу, более точно описывающую данные численности населения по годам. Формула имеет вид
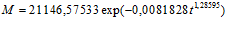(1)
Далее произведем расчет численности населения по данной формуле, и сравним расчетные данные с теоретическими. Найдем максимальную погрешность формулы. Результаты расчетов смотри в таблице 1.
Таблица 1. Численность населения по годам
| Год | Время
t, лет |
Числ. насл,
|
Расчетные значения: | ||
 |
ɛ |  ,% |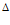
|||
| 2000 | 0 | 21700 | 21146.74 | 553.26 | 2.54 |
| 2001 | 1 | 21700 | 20974.30 | 725.7 | 3.34 |
| 2002 | 2 | 19723 | 20728.70 | -1005.7 | -5.09 |
| 2003 | 3 | 19700 | 20447.37 | -747.37 | -3.79 |
| 2004 | 4 | 19700 | 20141.82 | -441.82 | -2.24 |
| 2005 | 5 | 19800 | 19818.52 | -18.52 | -0.09 |
| 2006 | 6 | 19800 | 19481.72 | 318.28 | 1.60 |
| 2007 | 7 | 19700 | 19134.57 | 565.43 | 2.87 |
| 2008 | 8 | 19700 | 18779.48 | 920.52 | 4.67 |
| 2009 | 9 | 19690 | 18418.38 | 1271.62 | 6.45 |
| 2010 | 10 | 17253 | 18052.89 | -799.89 | -4.63 |
| 2011 | 11 | 17300 | 17684.36 | -384.36 | -2.22 |
| 2012 | 12 | 16930 | 17313.92 | -383.92 | -2.26 |
| 2013 | 13 | 16721 | 16942.59 | -221.59 | -1.32 |
| 2014 | 14 | 16624 | 16571.22 | 52.78 | 0.31 |
| 2015 | 15 | 16460 | 16200.58 | 259.42 | 1.57 |
| 2016 | 16 | 15831.32 | |||
| 2017 | 17 | 15464.05 | |||
| 2018 | 18 | 15099.29 | |||
Проведя расчет согласно формуле (1), получили расчетные данные площадей земель лесного фонда по годам:
-
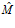- расчетная численность населения; -
ɛ- разность между теоретической численностью населения и расчетной;
-
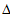,% – относительная погрешность формулы.
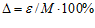
Максимальная погрешность формулы (1) является 6.45%. Значит, доверительная вероятность формулы составляет 93.55% [2]. Это хороший показатель можно продолжить расчет и прогнозировать численность населения. Как видите в таблице 1. Рассчитаны вероятная численность населения с 2016 по 2018 года. Для продолжения дальнейшего прогнозирования будем дополнять данные, и производить перерасчет каждый следующий год.
Библиографический список
- Мазуркин П.М. Математическое моделирование. Идентификация однофакторных статистических закономерностей: Учебное пособие П.М. Мазуркин, А.С. Филонов. Йошкар-Ола: МарГТУ, 2006. 292 с.
- Мазуркин. П.М. Статистическая эконометрика: Учебное пособие. Йошкар-Ола: МарГТУ, 2006. 376 с.
Количество просмотров публикации: Please wait