Введение.
В работе представлены результаты исследований, касающихся вопросов оптимизации характеристик интегрированных инвестиционных проектов. Поводом для проведения данных исследований послужили появившиеся в последнее время публикации (см., например, книгу Кириллов Ю.В., Досужева Е.Е. Методическое обеспечение оценки коммерческой эффективности инновационно-инвестиционных проектов. Барнаул, 2014 и работы этих авторов, представленные в списке литературы к ней), в которых сделана попытка сформулировать задачу нахождения наилучших соотношений (сочетаний) для параметров инвестиционных проектов в виде оптимизационных задач и предложить методы для их решения. Условимся предлагаемые в этой книге оптимизационные модели обозначать везде ниже идентификатором МДК_ОРТ, а на саму книгу ссылаться следующим образом: [ККД2014]. То есть запись, например, вида «[ККД2014], с. 130» означает отсылку на страницу 130 данной книги, а «см. модель МДК_ОРТ» – отсылает на одну из моделей авторов книги. 
В настоящей публикации содержатся результаты анализа некоторых методик оптимизации параметров инвестиционных проектов, они является продолжением исследований, посвященных вопросам оценивания эффективности интегрированных проектов, их оптимизации и управлению этими проектами [1].
Постановка задачи.
Положим, что в интегрированный проект (ИП) входят в качестве частных (основных, базовых) проектов проекты из следующих классов: продолжающихся проектов, заканчивающихся проектов, проектов, сменяющих другие проекты в рамках ИП и, наконец, новых оригинальных проектов (см. [2], [6], [16], [19] и др.). 
Требуется найти наилучшее сочетание параметров базовых и вспомогательных (неосновных, небазовых) проектов в смысле некоторых показателей эффективности ИП. Будем обозначать ИП как . 
Входные и выходные финансовые потоки проектов четырех классов ,  известны и имеют вид: , ,  – входные потоки (инвестиций, вложений) и ,  – выходные потоки (доходов). Полагаем, что оптимизацию параметров ИП  будем проводить на временном интервале ,  – время начала, а  – горизонт планирования и управления для ИП. В рассмотрение могут быть введены также проекты, в рамках которых происходит анализ и управление ИП. Они относятся к классу проектов  [2], [16]. 
Очевидно, финансовые потоки частных проектов могут перекрываться на интервалах , ,  и , , – это времена начала и окончания участия частных проектов в ИП. 
Обозначим обобщенные выходной и входной финансовые потоки ИП как  и ,  соответственно;  и  – элементы выходных и входных потоков проектов , , .
Если воспользоваться методом детализации финансовых потоков для оценивания дохода и доходности ИП, то это позволит учесть влияние основных и неосновных (внешних, вспомогательных) проектов друг на друга через финансовые потоки между ними. Тогда доход ИП может быть оценен величиной  – это накопленный в рамках неосновного (внешнего) проекта  (возможно, это проект, связанный с депозитным счетом в банке) общий доход ИП. Заметим, что свободные средства ИП могут быть проведены через неосновные или основные проекты в рамках ИП. Вспомогательные (неосновные) проекты могут быть как внешними, так и внутренними для анализируемого ИП. Общий доход ИП – это сумма значений доходов каждого проекта из класса . Так, для одного проекта  выполняется: ,  – доход ИП,  – ставка депозита для проекта .
Оптимизация параметров ИП.
В работе [ККД2014] (см., например, [ККД2014], с. 130, 133 и работы авторов, представленные в [ККД2014] в списке литературы) рассмотрена задача оптимизации ИП на основе показателей (чистого приведенного дохода),  (дисконтированного срока окупаемости),  (рентабельности). Как будет показано ниже, эта задача может быть существенно упрощена и найдено ее точное решение.
Итак, следуя обозначениям из [ККД2014], положим, что известны потоки проекта:  – входной поток (инвестиций) проекта (в обозначениях настоящей работы – это поток )=, для моментов времени , принимающих значения );  – длительность этапа инвестирования в проект;  – элементы выходного потока (доходов) проекта (в обозначениях данной работы – это поток , для моментов времени , принимающих значения );  – длительность этапа получения доходов от проекта;  – ставка дисконтирования или наращивания потоков проекта.
С использованием введенных в рассмотрение обозначений предлагается оценивать следующие показатели эффективности инвестиционного проекта (см. [ККД2014], с. 129 и др.).
Во-первых, по формуле

находится оценка показателя чистого приведенного дохода проекта.
Во-вторых, используя формулу
,

здесь  – это доходы проекта, приведенные ко времени ,
 ,
 – это все инвестиции проекта, приведенные ко времени , 
, 
 – ставка дисконтирования финансовых потоков проекта,
оценивается значение показателя дисконтированного срока окупаемости проекта.
Затем, в соответствии с формулой

, 

находится оценка рентабельности проекта (или дисконтированного индекса доходности). 
Наилучшее сочетание параметров проекта в моделях МДК_ОРТ предлагается находить, например, решая оптимизационную задачу. Формальный вид одной из таких задач следующий.
Требуется найти экстремум критериальных функций вида

 
 (1)

при ограничениях на элементы потоков проекта:

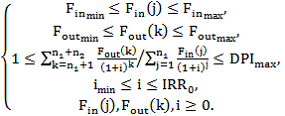 (2)

Здесь  – верхняя граница для ставки . 
К сожалению, модель МДК_ОРТ, представленная оптимизационной задачей (1)-(2), содержит много неточностей и опечаток. Рассмотрим подробнее основные из них.
Во-первых, показатели  и  являются функционально зависимыми и связанными. Таким образом, в задаче (1)-(2) можно оставить только один из двух показателей, например, , а другой () из задачи (1)-(2) исключить.
Во-вторых, решение задачи (1)-(2) является тривиальным, и оно имеет вид: ,   Здесь, в отличие от модели МДК_ОРТ, для каждой из переменных  и  введены свои нижние и верхние границы.
Далее, следует заметить, что задача (1)-(2) включает в себя показатель , который, на самом деле, не оценивает срок окупаемости проекта. Можно легко показать, что формула для  
,

оценивает значение срока окупаемости для другого (можно сказать, «искусственного») проекта. Это обстоятельство объясняется тем, что при выводе формулы для  была произведена замена исходного выходного потока проекта на другой поток, причем, последний к исходному проекту абсолютно никакого отношения не имел. 
Еще следует заметить, что задача (1)-(2) поставлена некорректно с экономической точки зрения. Хорошо известно, что элементы выходного потока проекта (доходы проекта, искомые переменные задачи – ) зависят от элементов входного потока (затрат, инвестиционных вложений, искомые переменные задачи – ). В таком случае в число ограничений задачи (1)-(2) необходимо ввести ограничения, связывающие искомые переменные  и . 
Еще одно немаловажное обстоятельство связано с тем, за счет чего могут быть снижены затраты (вложения, издержки, объемы инвестиций) проекта до оптимальных значений , и увеличена доходная часть проекта до оптимальных значений )? На практике, как правило, сначала решают вопрос об источниках снижения издержек (затрат) и увеличении доходов. Затем в соответствии с этими изменениями пересчитывают показатели эффективности проекта. Снижение затрат проекта () может быть осуществлено, например, через выбор новых источников финансирования, новых схем расчета по кредитам и т.д. Обычно задача оптимизации параметров проекта является дискретной, алгоритм ее решения – это перебор (возможно, направленный) вариантов инвестиционных схем реализации проекта. Увеличение доходов проекта () можно осуществить, например, повышая цены на производимую продукцию. 
Заметим, что в ограничении  на значение рентабельности  ограничение сверху является лишним. Его можно заменить на эквивалентное ему ограничение . 
Исходя из экономического смысла искомых переменных задачи (1)-(2), должны выполняться неравенства: ,  и ,  отсюда следует, что ограничения  и  являются лишними. Аналогично следует пересмотреть и ограничение на ставку дисконтирования  .
Учитывая вышесказанное, оптимизационную задачу (1)-(2) можно существенно упростить. Вот один из вариантов такой упрощенной формы для задачи (1)-(2).
Требуется найти максимальное значение критерия 

 (3)

при ограничениях на элементы потоков проекта:

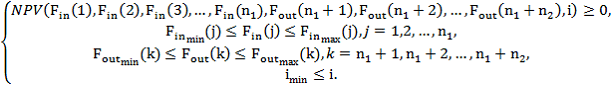(4)

Решение упрощенной задачи (3)-(4) совпадает с решением исходной задачи (1)-(2) и имеет вид: 
,  
Управление свободным капиталом и заимствованиями.
В работе [ККД2014] (см. [ККД2014], с. 137, 139, 141 и др.) рассмотрены оптимизационные модели, в которых отражены используемые в проектах собственные (СК) и заемные (ЗК) средства. Так, например, в ней введены в рассмотрение ограничения на искомые элементы финансовых потоков проекта вида . Такие ограничения должны подчеркнуть то обстоятельство, что входной поток проекта формируется за счет собственного капитала в объеме СК. Следует, однако, заметить, что СК является (как и финансовые потоки проекта вообще) динамической характеристикой проекта. Более того, СК формируется (образуется) элементами финансовых потоков ИП, т.е. зависит от них, является производной от них. Заметим, что процесс взаимного влияния финансового потока и СК таков, что сначала за счет потока формируется поток доходов (выходной поток проекта) , на его основе формируется СК, а затем (в следующие моменты времени) за счет СК генерируются элементы входного финансового потока . 
Условно и схематично такие преобразования потоков и их взаимное влияние друг на друга можно представить, например, следующим образом:

Аналогичные замечания можно сделать и относительно ограничений вида  (см., например, [ККД2014], с. 139 и др.). Ограничения такого вида должны были подчеркнуть, что входной финансовый поток  порождается только заемными средствами в количестве ЗК. 
Отметим, что процесс взаимодействия финансовых потоков, СК и ЗК в общем случае достаточно сложен. Аналогично тому, как это было сделано для отражения влияния СК на элементы финансовых потоков проекта, представим схему влияния на них СК и ЗК:

Попытки описать такое взаимодействие сделаны, например, в работах [2], [3], [12], [13], [14], [16], [20].
В [ККД2014, с. 144 и др.] для решения многокритериальных оптимизационных задач предлагается использовать метод нормализации критериев. Однако показано, что этот метод является S_p-неустойчивым и на практике им пользоваться, к сожалению, нельзя. Подробнее об этом свойстве метода нормализации критериев изложено в работах [5], [8], [10].

Выводы. 
В работе рассмотрены слабые позиции некоторых методик оптимизации параметров ИП.
Предложены к рассмотрению методики и сделаны ссылки на соответствующие публикации, в которых рассмотрены подходы, позволяющие обойти эти проблемы.
В основу предлагаемых схем оптимизации ИП положены критерии и методики, основанные на методе детализации финансовых потоков проектов.

1. Наумов А.А., Наумова А.А., Ветров А.Н. О проблемах некоторых методик оценивания эффективности интегрированных проектов// Современные научные исследования и инновации. 2015. № 10 [Электронный ресурс]. URL: http://web.snauka.ru/issues/2015/10/58835 (дата обращения: 02.11.2015).
2. Наумов А.А., Наумова А.А. Новый подход к оцениванию доходности и оптимизация интегрированных проектов// Современные научные исследования и инновации. 2015. № 8 [Электронный ресурс]. URL: http://web.snauka.ru/issues/2015/08/57215 (дата обращения: 31.08.2015).
3. Наумов А.А., Наумова А.А. О некорректности одной модели оптимизации структуры капитала// ISJ Theoretical&Applied Science, Materials of the ISPC «European Innovation», 30.09.2014, Martigues, France. 2014. № 9 (17). С. 170-173.
4. Наумов А.А., Наумов Ал.А. Контекстная зависимость инвестиционных проектов и оптимизация их параметров// ISJ Theoretical&Applied Science, Materials of the ISPC «European Scientific Achievements», 30.10.2014, Brighton, UK. 2014. № 10 (18). С. 56-58.
5. Наумов А.А. К проблемам метода нормализации критериев в задачах векторной оптимизации// Theoretical&Applied Science, Materials of the ISPC «Theory and Practice», 30.08.2013, Munich, Germany. 2013. № 8 (4). С. 24-26.
6. Наумов А.А. К моделям совместного управления проектами// Theoretical&Applied Science, Materials of the ISPC «Theory and Practice», 30.08.2013, Munich, Germany. 2013. № 8 (4). С. 87-89.
7. Наумов А.А. К аналитическим решениям некоторых экономико-математических задач// Theoretical&Applied Science, Materials of the ISPC «Results &Perspectives», 30.09.2013, Florence, Italy. 2013. № 9 (5). С. 93-97.
8. Наумов А.А. К S_p-неустойчивости метода нормализации критериев решения многокритериальных задач оптимизации// Theoretical&Applied Science, Materials of the ISPC «Results &Perspectives», 30.09.2013, Florence, Italy. 2013. № 9 (5). С. 14-16.
9. Наумов А.А., Крюков С.В. К проблемам одной модели управления совместными инвестиционными проектами// Финансовая аналитика: проблемы и решения. 2013. № 40 (178). С. 53-56.
10. Наумов А.А. К свойству S_p-инвариантности методов решения многокритериальных задач оптимизации// Theoretical & Applied Science, Materials of the ISPC «Advances in techniques&technologies», 30.10.2013, Milan, Italy. 2013. №10(6). С. 1-4.
11. Наумов А.А. Перераспределение общего дохода между участниками интегрированного проекта// Theoretical & Applied Science, Materials of the ISPC «Advances in techniques&technologies», 30.10.2013, Milan, Italy. 2013. №10(6). С. 129-132.
12. Наумов А.А. Оптимизация структуры заимствований и вложений доходов инвестиционного проекта// Theoretical & Applied Science, Materials of the ISPC «Advances in techniques&technologies», 30.10.2013, Milan, Italy. 2013. №10(6). С. 133-136.
13. Наумов А.А. К вопросу об упрощении двух задач оптимизации инвестиций// Финансовая аналитика: проблемы и решения. 2013. № 46 (184). С. 26-30.
14. Наумов А.А., Наумова А.А. Оценивание эффективности интегрированных проектов на основе метода детализации финансовых потоков// Современные научные исследования и инновации. 2015. № 7 [Электронный ресурс]. URL: http://web.snauka.ru/issues/2015/07/56645 (дата обращения: 31.07.2015).
15. Наумов А.А., Наумова А.А. К оцениванию эффективности интегрированных проектов// Современные научные исследования и инновации. 2015. № 8 [Электронный ресурс]. URL: http://web.snauka.ru/issues/2015/08/56856 (дата обращения: 25.08.2015).
16. Наумов А.А., Наумова А.А. Новый подход к оцениванию доходности и оптимизация интегрированных проектов// Современные научные исследования и инновации. 2015. № 8 [Электронный ресурс]. URL: http://web.snauka.ru/issues/2015/08/57215 (дата обращения: 31.08.2015).
17. Наумов А.А., Наумова А.А. Анализ эффективности инвестиционных проектов с учетом инфляции// Экономика и менеджмент инновационных технологий. 2015. № 5 [Электронный ресурс]. URL: http://ekonomika.snauka.ru/2015/05/8887  (дата обращения: 15.06.2015).
18. Наумов А.А., Наумова А.А. К оцениванию эффективности инновационных проектов на основе метода детализации финансовых потоков// ISJ Theoretical&Applied Science, Materials of the ISPC «Education & Innovation», 30.06.2015, Avignon, France. 2015. № 6 (26). С. 85-94.
19. Наумов А.А. Теоретические и прикладные вопросы моделирования бизнес-процессов. Модели, алгоритмы, программы. LAP LAMBERT Academic Publishing, 2012.
20. Наумов А.А. Методы анализа и синтеза инвестиционных проектов. Эффективность, риски, управление. LAP LAMBERT Academic Publishing, 2013.
21. Наумов А.А. Управление портфельными инвестициями. Эффективность, риски, оптимизация. LAP LAMBERT Academic Publishing, Saarbrucken, 2014.
22. Наумов А.А., Баженов Р.И. О проблемах классических показателей эффективности инвестиционных проектов// Современные научные исследования и инновации. 2014. № 11 [Электронный ресурс]. URL: http://web.snauka.ru/issues/2014/11/40825  (дата обращения: 20.11.2014).
23. Список трудов. [Электронный ресурс]. URL: https://sites.google.com/site/anatolynaumov2011/home/spisok-trudov-list-of-papers (Дата обращения 23.11.15).

Все статьи автора «Наумов Анатолий Александрович»