Следует:определить величину начального накопленного суммарного кинетического момента системы инерционных исполнительных органов, при котором за заданное время (полчаса) можно совершить разворот космического аппарата, максимально быстро по времени, с использованием инерционных исполнительных органов – маховиков в любом пространственном направлении, так как в разные времена года необходимы различные направления разворота космического аппарата. 
проверить для требуемых значений накопленного суммарного кинетического момента системы инерционных исполнительных органов времена разворота для двух способов максимальных по быстродействию разворотов – плоского разворота вокруг оси Эйлера и разворот с максимальной текущей проекцией угловой скорости на вектор конечного разворота. 
Рассматривается система инерционных исполнительных органов, состоящая из 4-х маховиков, оси вращения которых перпендикулярны разным граням правильного многогранника тетраэдра. При этом область вариации кинетического момента системы ИИО в первом приближении представляет собой шар радиуса R = 1.633 h, где h – модуль вектора кинетического момента одного маховика при его максимальной скорости вращения. 
Рассмотрение продолжительности времени разворота проводится для случая разворотов относительно инерциальной системы координат. Кинематические уравнения задаются в кватернионной форме. Применятся следующий способ разворота: [3], [4]- плоский разворот вокруг вектора конечного поворота с максимальной угловой скоростью (рис.1). 

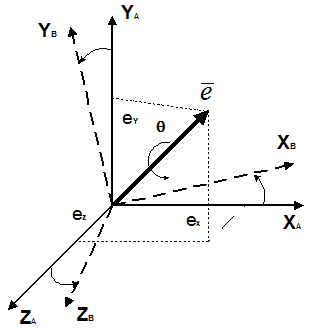
Рисунок1. Эйлерова ось вращения , определяющая поворот системы координат. Здесь  - инерциальная, а  – связанная системы координат.

Обозначим суммарный вектор накопленного кинетического момента космического аппарата и инерционных исполнительных органов через . Считаем, что за время разворота приращением вектора за счет действия моментов внешних сил можно пренебречь. Тогда вектор остается неизменным в инерциальной СК.
Из кватерниона рассогласования положения космического аппарата, найдём мгновенную ось разворота, относительно которой для оптимальности времени будем совершать плоский разворот в пространстве:  .
Обозначим угловую скорость вокруг вектора конечного поворота через . Тогда , где через H обозначен суммарный кинетический момент инерционные исполнительные органы, а через  тензор моментов инерции космического аппарата. При развороте с максимальной угловой скоростью модуль вектора  равен . В этом случае получаем уравнение . Решая его, найдем [4]: 

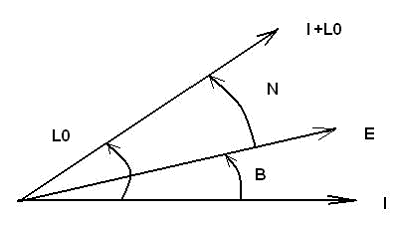
Рисунок2. Связь между связанной системой координат  и инерциальной  , с учётом кватерниона разворота .

Второй способ – пространственный разворот с максимальной текущей проекцией угловой скорости на вектор конечного разворота. Введём новые обозначения для нового способа решения (см. рис. 2). Данный способ предложен Чертоком М.Б. (РКК «Энергия» им. С.П. Королева). В данном способе найдем угловую скорость разворота, минимизировав функции , при условии . Решая задачу методом множителей Лагранжа, найдем компоненты вектора :

Далее найдем угловую скорость разворота[2] 
Результаты.
Проводилось математическое моделирование двух вариантов разворотов КА. 
Максимальный управляющий момент системы ИИО полагался равным (управляющий момент системы маховиков в произвольном направлении). Тензор моментов инерции считался диагональным (центробежные моменты инерции отсутствуют). При этом максимальное угловое ускорение, создаваемое системой маховиков вокруг вектора конечного поворота составляет[3,4]:

Здесь R = 30 Нмс,- максимальный кинетический момент создаваемый корпусом КА. 

Использовались следующие варианты начального накопленного суммарного кинетического момента, при которых выполняется сходимость метода и удовлетворяются точности по углу разворота и угловым скоростям:2) ,3)  Разворот проводился по 26 различным направлениям, с углом разворота 180°[1].

Табл.1. Требуемые времена разворота для различных направлений разворота и начального суммарного кинетического момента.

1)В 34 случаях предпочтительнее первый метод, а в 44 случаях – второй метод.
2)Вместе с тем из таблицы видно, что времена разворота приблизительно одинаковы в большинстве случаев разворотов, и отличаются, как правило, на 5—10%. 
3)Все три набора начального суммарного кинетического момента удовлетворяют требованию ограничения времени разворота, за исключением трёх пространственных направлений, что обусловлено тензором инерции КА, причём отличие составляет 8 %, что входит в допуск. Таким образом, искомая величина начального суммарного кинетического момента составляет ~_.
4) С точки зрения простоты вычислений, а, следовательно, и используемых ресурсов бортовой ЦВМ предпочтительнее первый метод.

Заключение.

Проведено сравнение двух способов разворота КА за минимальное время. 
Для каждого из способов написана программа на языке СИ. 
Приведены результаты для различных вариантов начального суммарного кинетического момента и различных траекторий разворота. 
Выбран способ разворота для бортового алгоритма.
Выбрана величина начального суммарного кинетического момента

1. Алиев-Хетагов Р. С. Расчёт продолжительности оптимального по времени разворота космического аппарата при смене режимов ориентации. Вестник СибГАУ. №5(45)/2012.
2. Бранец В.Н., Казначеев Ю.В., Черток М.Б. Оптимальный разворот твердого тела с одной осью симметрии. Космические исследования. Том XXII вып.3. -М. Наука 1984г.
3. Платонов В.Н. О точности стабилизации космического аппарата дистанционного зондирования Земли без использования информации инфернальных датчиков. Космическая  техника и технологии. №3(6)/2014
4. Платонов В.Н. Одновременное управление движением центра масс и вокруг центра масс при манёврах космических аппаратов на геостационарной и высокоэллиптических орбитах с использованием электрореактивных двигателей. Космическая  техника и технологии. №1/2013

Все статьи автора «Алиев-Хетагов Рашид Саядуллаевич»