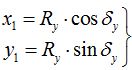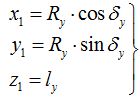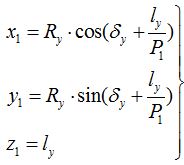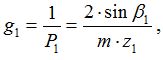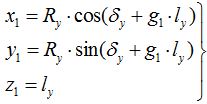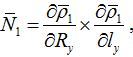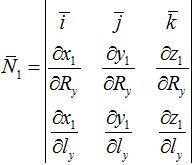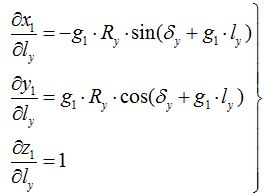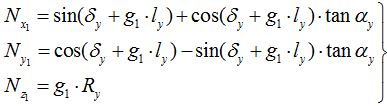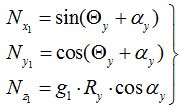При решении задач проектирования зуборезного обкатного инструмента [1-2] предполагается, что его режущие кромки располагаются на некоторой инструментальной поверхности (ИИП), при этом ИИП и обрабатываемая поверхность изделия в точке контакта имеют общую касательную, а соответственно и общую нормаль. Тогда, если контакт двух сопряженных поверхностей непрерывен, в точках контакта нормальная составляющая скорости относительного движения поверхностей равна нулю. Аналитически это выражение записывается так [4-6]:

                                                                   (1)

На основе уравнения (1) базируется кинематический метод определения уравнения поверхности, огибающей боковую поверхность зуба зубчатого колеса (ЗК).

Ранее, в работе [3],  были определены проекции вектора относительной скорости V . В настоящей работе рассмотрим вывод зависимостей вектора нормали N к профилю ЗК. Для чего необходимо задать параметры зубчатой дели.

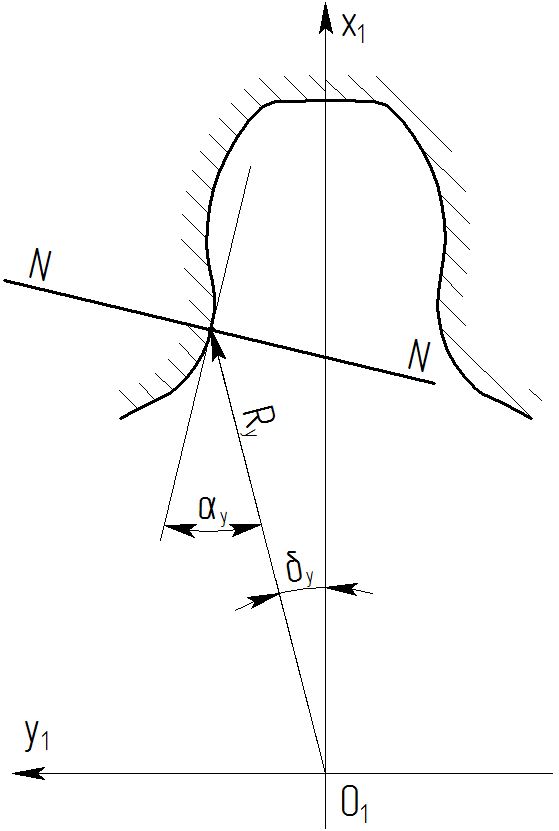
В общем случае, параметры зубчатого колеса внутреннего зацепления будем определять следующими параметрами:

• R­­­_y – радиус текущей точки;
• δ_y – полярный угол относительно выбранного начального положения;
• α_y – угол между радиус-вектором и касательной к профилю.

Значения δ_y и α_y имеют положительные значения профиля, как указано на рис.1. Для противоположной стороны профиля значения этих углов изменяются на противоположные.

Рисунок 1 – Параметры зубчатого колеса внутреннего зацепления

Тогда уравнение профиля зубчатого колеса в торцовой плоскости в подвижной системе детали O₁x₁y₁z₁, ось z₁ которой жестко связанна с осью ЗК, будет записана в виде системы уравнений (2).

                                                                                                                (2)

Теперь перейдем от торцового профиля к определению винтовой поверхности. Образование эвольвентной винтовой поверхности схематически показано на рис. 2. Для определенности будем считать, что профиль располагается на правой винтовой поверхности. Введем координату l_y, определяющую расстояние от торцовой плоскости до рассматриваемой точки в направлении оси z₁.

                                                                                                     (3)

Рисунок 2 – Образование эвольвентной винтовой поверхности зуба колеса

Дадим профилю винтовое движение относительно оси z₁ с параметром P₁. При этом, поворот профиля на некоторый угол φ_y обусловит перемещение вдоль оси z₁ на величину (4).

                                                                                                       (4)

Тогда уравнение винтовой поверхности можно записать в виде:

                                                                                                         (5)

Или с учетом формулы (4), из которой следует, что:

то:

                                                                                          (6)

Учитывая широкое распространение прямозубых колес, параметр P₁ удобно заменить на обратную ему величину:

                                                                                        (7)

где β₁ – угол наклона винтовой линии зубьев изделия.

Тогда при значении β₁ = 0 отпадает необходимость определения значения P₁ = ∞.

                                                                                          (8)

Определим координаты вектора нормали к боковой поверхности зубьев зубчатого колеса. Вектор нормали определяется по формуле (9).

                                                                                            (9)

cчитая винтовую поверхность векторной функцией криволинейных координат R_y и l_y:

                                                                                              (10)

                                                                                                  (11)

Найдем входящие в определитель частные производные, учитывая что:

                                                                                                 (12)

                                                                                                                                                 (13)

                                                                                                                                                  (14)

Отсюда следует:

                                                                                                                                                    (15)

Упростим уравнения, учитывая при этом, что:

                                                                                                                                                    (16)

Тогда получим:

                                                                                                                                                     (17)

Полученные расчетные зависимости для определения вектора нормали к профилю изделия необходимы для решения задачи профилирования обкаточного резца – определения кинематическим методом уравнения поверхности, огибающей боковую поверхность зуба ЗК.

1. Цвис Ю.В. Профилирование режущего обкатного инструмента. М.: МАШГИЗ, 1961. – 156с.
2. Волков Н.Н. Исследование и разработка инструмента для нарезания цилиндрических зубчатых колес с внутренними зубьями по методу зуботочения.: Дис. канд. тех. наук. – М., 1981. – 222с.
3. Кирютин А.С. Векторный метод определения скорости относительного движения при проектировании обкаточных резцов для обработки эвольвентных зубчатых колес внутреннего // Машиностроитель. 2015. № 7. – С. 15-19, ил. 2.
4. Литвин Ф.Л. Теория зубчатых зацеплений. М.: «НАУКА», 1968. – 584с.: ил.
5. Производство зубчатых колес: Справочник / С.Н. Калашников, А.С. Калашников, Г.И. Коган и др.; Под общ. Ред. Б.А. Тайца. – 3-е изд., перераб. И допол. – М.: Машиностроение, 1990. – 464с.: ил.
6. Радзевич С.П. Кратко о кинематическом методе и об истории уравнения контакта в форме n · V = 0 // Теория механизмов и машин. 2010. №1. Том 8 [Электронный ресурс]. URL:http://tmm.spbstu.ru/15/radzevich_15.pdf
7. Петухов Ю.Е. Формообразование численными методами / Ю.Е. Петухов. – М. : «Янус-К», 2004. – 200 с.
8. Гречишников В.А. Математическое моделирование в инструментальном производстве / Гречишников В.А., Колесов Н.В., Петухов Ю.Е.. – М. : МГТУ «СТАНКИН». УМО АМ, 2003. – 116 с.
9. Петухов Ю.Е. Проектирование инструментов для обработки резанием деталей с фасонной винтовой поверхностью на стадии технологической подготовки производства : дис. … докт. техн. наук : 05.03.01 / Петухов Ю.Е.. – М., 2004. – 393с.
10. Петухов Ю.Е. Численные модели режущего инструмента для обработки сложных поверхностей / Петухов Ю.Е., Колесов Н.В. // Вестник машиностроения. – 2003. – №5. – С. 61-63.
11. Петухов  Ю.Е. Профилирование режущих инструментов среде Т-flex CAD-3D / Петухов Ю.Е. // Вестник машиностроения. – 2003. – №8. – С. 67-70.
12. Петухов Ю.Е. Способ формообразования фасонной винтовой поверхности стандартным инструментом прямого профиля / Петухов Ю.Е., Домнин П.В. // Вестник МГТУ «СТАНКИН». – 2011. – №3. – С. 102-106.
13. Колесов Н.В. Система контроля сложных кромок режущих инструментов / Колесов Н.В., Петухов Ю.Е. // ИТО: Инструмент. Технология. Оборудование. – 2003. – №2. – С. 42-45.
14. Петухов Ю.Е. Компьютерная модель формообразования сложной поверхности / Петухов Ю.Е., Домнин П.В. // Международная научно-техническая конференция «Автоматизация: проблемы, идеи, решения». В 2 т. : сб. науч. ст. – Тула, 2010. – Т. 1. – С. 197-200.
15. Колесов Н.В. Компьютерная модель дисковых фасонных затылованных фрез / Колесов Н.В., Петухов Ю.Е., Баринов А.В. // Вестник машиностроения. – 1999. – №6. – С. 57-61.
16. Петухов Ю.Е. Решение обратной задачи профилирования на базе схемы численного метода заданных сечений /Петухов Ю.Е., Домнин П.В. // Справочник. Инженерный журнал с приложением. – 2011. – №11. – С. 26-29.
17. Колесов Н.В. Математическая модель червячной фрезы с протуберанцем / Колесов Н.В., Петухов Ю.Е. // СТИН. – 1995. – №6. – С. 26-29.
18. Колесов  Н.В. Два типа компьютерных моделей режущего инструмента Колесов/ Н.В., Петухов Ю.Е. // СТИН. – 2007. – №8. – С. 23-26.
19. Петухов Ю.Е. Точность профилирования при обработке винтовой фасонной поверхности / Ю.Е. Петухов, П.В. Домнин // СТИН. – 2011 – №7. – С. 14-17.
20. Петухов Ю.Е., Математическая модель криволинейной режущей кромки спирального сверла повышенной стойкости / Ю.Е. Петухов, А.А. Водовозов // Вестник МГТУ «СТАНКИН». – 2012. – №3. – С. 28-32.
21. Петухов Ю.Е. Некоторые направления развития САПР режущего инструмента / Ю.Е. Петухов // СТИН. – 2003. – №8. – С. 26-30.
22. Петухов  Ю.Е. Затачивание по передней поверхности спиральных сверл с криволинейными режущими кромками / Ю.Е. Петухов, А.А. Водовозов // Вестник МГТУ «СТАНКИН». – 2014. – №1 (28). – С. 39-43.
23. Петухов Ю.Е. Cпособ шлифования фасонных валов. Патент на изобретение RUS 863310  04.05.1979
24. Петухов Ю.Е. Задачи по формообразованию при обработке резанием /Петухов Ю.Е., Колесов Н.В., Юрасов С.Ю.// Вестник машиностроения. 2014. № 3. С. 65-71.
25. Петухов Ю.Е. Определение задних кинематических углов при обработке винтовых фасонных поверхностей стандартными фрезами прямого профиля./ Петухов Ю.Е., Домнин П.В.// Вестник МГТУ Станкин. 2014. № 2 (29). С. 27-33
26. Петухов Ю.Е. Устройство для правки фасонных шлифовальных кругов. Патент на изобретение RUS 823101 21.03.1979
27. Петухов Ю.Е. Способ обработки цилиндрических поверхностей патент на изобретение RUS 904999 04.05.1979
28. Петухов Ю.Е. Компьютерное моделирование обработки винтовой канавки на заготовке концевой фрезы./ Петухов Ю.Е, Домнин П.В.// Известия Московского государственного технического университета МАМИ. 2011. № 2. С. 156-164.
29. Петухов Ю.Е. Прибор для профилирования червячных фрез. Патент на изобретение RUS 878467 07.12.1978
30. Petukhov, Y.E. Shaping precision in machining a screw surface / Y.E. Petukhov, P.V. Domnin // Russian Engineering Research. – 2011. – T. 31. – №10. – С. 1013-1015.
31. Kolesov, N.V. Computer models of cutting tools / N.V. Kolesov, Y.E. Petukhov // Russian Engineering Research. – 2007. – T. 27. – №11. – С. 812-814.
32. Petukhov, Y.E. Determining the shape of the back surface of disc milling cutter for machining a contoured surface / Y.E. Petukhov, A.V. Movsesyan // Russian Engineering Research. – 2007. – T. 27. – №8. – С. 519-521.
33. Petukhov Yu.E. Some directions of cutting tool cad system development./ Petukhov Yu.E.// Russian Engineering Research. 2003. Т. 23. № 8. С. 72-76.
34. Petukhov Yu.E. Curvilinear cutting edge of a helical bit with uniform life./ Petukhov Yu.E.// Russian Engineering Research. 2014. Т. 34. № 10. С. 645-648.
35. Kolesov N.V. The mathematical model of a hob with protuberances./Kolesov N.V., Petukhov Yu.E.// Russian Engineering Research. 1995. Т. 15. № 4. С. 71-75.
36. Engineering Research. – 2007. – T. 27. – №8. – С. 519-521.
37. Petukhov Yu.E. Geometric shaping in cutting./ Petukhov Yu.E., Kolesov N.V., Yurasov S.Yu.// Russian Engineering Research. 2014. Т. 34. № 6. С. 374-380.

Все статьи автора «Кирютин Алексей Сергеевич»