Граф G есть средство описания связей между объектами, это совокупность непустого множества вершин ![]() и наборов множества пар вершин (ребер, соединяющих вершины)
и наборов множества пар вершин (ребер, соединяющих вершины) ![]() . Каждое ребро
. Каждое ребро ![]() соединяет две вершины, которые называют соседними и обозначается так [1]:
соединяет две вершины, которые называют соседними и обозначается так [1]:
![]()
где ![]() – вершины графа. Если
– вершины графа. Если ![]() совпадают, т.е.
совпадают, т.е. ![]() то такое ребро называют петлей.
то такое ребро называют петлей.
Если граф неориентированный, то множество ![]() пар вершин может быть неупорядоченным, если же граф является ориентированным, то множество пар вершин упорядочено, обозначается буквой
пар вершин может быть неупорядоченным, если же граф является ориентированным, то множество пар вершин упорядочено, обозначается буквой ![]() , а ориентированные ребра называют дугами. Каждая дуга
, а ориентированные ребра называют дугами. Каждая дуга ![]() обозначается так:
обозначается так:
![]()
где ![]() – начало, а
– начало, а ![]() – конец дуги.
– конец дуги.
Существуют смешанные графы ![]() где
где ![]() определены аналогично. В таких графах некоторые ребра могут быть как ориентированными, так и неориентированными.
определены аналогично. В таких графах некоторые ребра могут быть как ориентированными, так и неориентированными.
Граф, в котором каждому ребру поставлено в соответствие некое значение, называется взвешенным. Это значение называют весом ребра. Чаще всего данное значение входит в множество вещественных чисел, в данном случае его можно интерпретировать как «длину» или «пропускную способность» соответствующего ребра.
Если ребро e соединяет две вершины u, v, то говорят, что ребро e и вершина u , а также ребро e и вершина v инцидентны. Две вершины, инцидентные одному ребру называются соседними или смежными. Ребра, инцидентные одной вершине, также называются смежными.
Существуют несколько способов представления графа:
– в виде таблицы, где как столбцы, так и строки соответствуют вершинам графа. В каждой ячейке такой матрицы записывается число, указывающее на наличие связи от вершины-строки к вершине-столбцу. В случае взвешенного графа число равняется весу соответствующего ребра. Такую таблицу называют матрицей смежности;
– в виде таблицы, где строки соответствуют вершинам графа, а столбцы соответствуют его ребрам. Ненулевое значение в ячейке указывает на наличие связи между вершиной и ребром. В случае ориентированного графа в ячейку (i,j)ставится «1» в случае, если i является началом дуги j , «-1» если концом и «0» если связь между вершиной и ребром отсутствует. Такую таблицу называют матрицей инцидентности;
– в виде списка, где каждой вершине графа соответствует строка, в которой хранится список смежных вершин. Такую совокупность называют списком смежности;
– в виде списка, где каждому ребру графа соответствует пара вершин, инцидентных ребру. Такой список называется списком ребер.
Используя собранные данные по транспротной системе Архангельской области построим взвешенный граф и использовать алгоритм Дейкстры для обоснования рентабельности возможных проектов реализуем модель в Microsoft Excel.
Алгоритм голландского ученого Эдсгера Дейкстры позволяет найти кратчайшие пути из одной изначально заданной вершины графа до всех остальных, так что его удобно использовать для задачи поиска оптимального маршрута.
Данный алгоритм пошагово перебирает все вершины графа и назначает им метки, которые являются минимальным расстоянием от вершины источника до конкретной вершины.
Главное ограничение данного алгоритма заключается в использовании исключительно положительных значений ребер, отрицательные веса приведут к некорректному решению. Т.к. весом ребер в модели являются расстояние или средняя скорость, отрицательных значений вес никогда не принимает, что означает, что данный алгоритм можно использовать.
Применительно к данной задаче, алгоритм Дейкстры не имеет существенных преимуществ или недостатков по сравнению другими алгоритмами, которые решают ту же задачу другими способами, например, алгоритмом Левита или алгоритмом Форда-Беллмана, так что на практике возможно использование любого из имеющихся алгоритмов.
Следует отметить, что результаты моделирования транспортной сети на примере Архангельской области были представлена авторами в виде взвешенного графа, где вершины – населенные пункты, а ребра – дороги, имеющие в качестве «веса» 2 параметра: протяженность веток и понижающий коэффициент, определяющий среднюю скорость передвижения.[5,6]
Рассмотрим проектирование дополнительных трасс в пределах рассматриваемого региона на примере трассы Архангельск (Мезень) – Нарьян-Мар
В данном случае речь идет о строительстве «с нуля» двухполосной асфальтированной трассы, т.к. на данный момент не существует ни железнодорожной, ни автомобильной, ни даже гравийной или грунтовой дороги, напрямую соединяющие Ненецкий автономный округ с остальной Архангельской областью (зимники не учитываются). Связь осуществляется через авиа и морской транспорт, что не может в полной мере компенсировать отсутствие транспортной инфраструктуры, особенно учитывая, что последний также недоступен зимой. Из-за высокой стоимости доставки продуктов в цены на них в заполярном городе являются одними из самых высоких в стране, так что необходимость автомобильной дороги очевидна.
Автомобильная трасса, соединяющая с областным центром через Мезень, позволила бы избавить Ненецкий автономный округ от изолированности, стать толчком для развития региона и заметно улучшить уровень жизни населения.
Второй рассматриваемый проект – это асфальтирование автодорожных веток Северодвинск – Онега и Онега – Плесецк
Асфальтовая дорога между Северодвинском и Онегой позволила бы увеличить пропускную способность (и среднюю скорость движения) между Онегой и двумя крупными городами — Архангельском и Северодвинском, исключив пробки и заметно развив транспортную инфраструктуру региона, а дорога Онега–Плесецк позволила бы к тому же соединить два важнейших военных объекта друг с другом, что также важно в нынешней непростой политической обстановке.
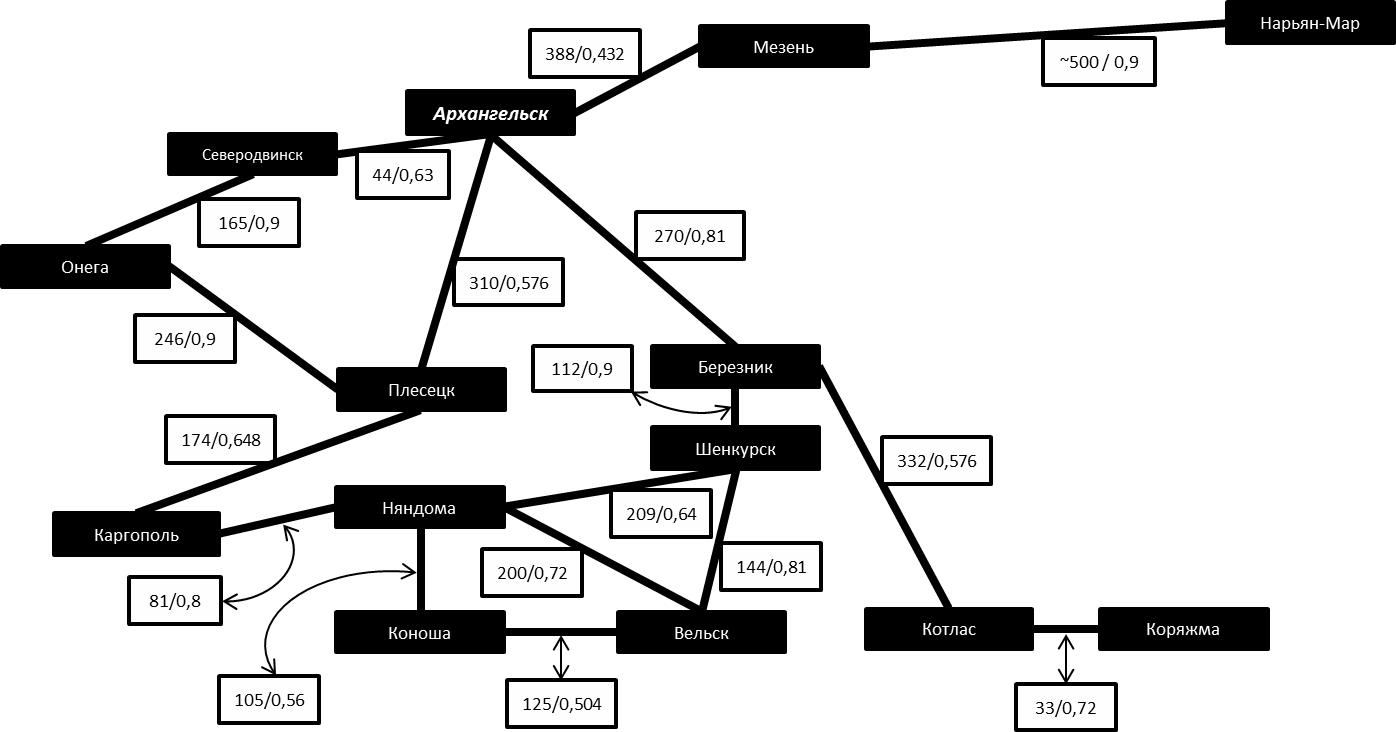
Следует отметить, что среднее время в пути среднестатистического грузового автомобиля по маршруту Северодвинск-Онега-Плесецк при соблюдении всех правил по сравнению с нынешним оптимальным маршрутом Северодвинск-Архангельск-Плесецк [5,6] уменьшится чуть менее чем на 25% (рис. 1).
Рисунок 1 – Граф автомобильных дорог с учетом проектов
Определим матрицу смежности графа (с учетом рассматриваемых проектов):
Таблица 1 – Матрица смежности графа (в час.)
|
Матрица смежности |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
|
|
Мезень |
1 |
- |
- |
12,83 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
7,94 |
|
Северодвинск |
2 |
- |
- |
1,00 |
2,62 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
|
Архангельск |
3 |
12,83 |
1,00 |
- |
- |
4,76 |
7,69 |
- |
- |
- |
- |
- |
- |
- |
- |
|
Онега |
4 |
- |
2,62 |
- |
- |
- |
3,90 |
- |
- |
- |
- |
- |
- |
- |
- |
|
Березник |
5 |
- |
- |
4,76 |
- |
- |
6,88 |
1,78 |
- |
- |
0,16 |
- |
- |
- |
- |
|
Плесецк |
6 |
- |
- |
7,69 |
3,90 |
6,88 |
- |
- |
- |
0,07 |
- |
- |
- |
- |
- |
|
Шенкурск |
7 |
- |
- |
- |
- |
1,78 |
- |
- |
4,67 |
- |
- |
2,54 |
- |
- |
- |
|
Няндома |
8 |
- |
- |
- |
- |
- |
- |
4,67 |
- |
1,45 |
- |
3,97 |
2,68 |
- |
- |
|
Каргополь |
9 |
- |
- |
- |
- |
- |
3,84 |
- |
1,45 |
- |
- |
- |
- |
- |
- |
|
Котлас |
10 |
- |
- |
- |
- |
8,23 |
- |
- |
- |
- |
- |
- |
- |
0,65 |
- |
|
Вельск |
11 |
- |
- |
- |
- |
- |
- |
2,54 |
3,97 |
- |
- |
- |
3,54 |
- |
- |
|
Коноша |
12 |
- |
- |
- |
- |
- |
- |
- |
2,68 |
- |
- |
3,54 |
- |
- |
- |
|
Коряжма |
13 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
0,65 |
- |
- |
- |
- |
|
Нарьян-Мар |
14 |
7,94 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
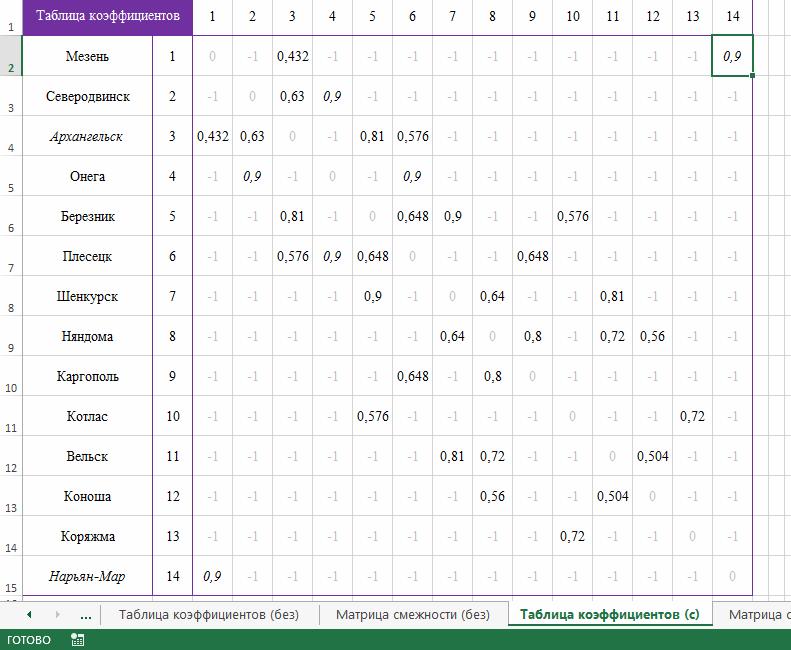
Значения матрицы смежности, с которой будет работать макрос в M.Excel, зависят от выбранного транспорта и коэффициента для соответствующего ребра (рисунок 2).
|
|
Рисунок 2 - Таблица коэффициентов
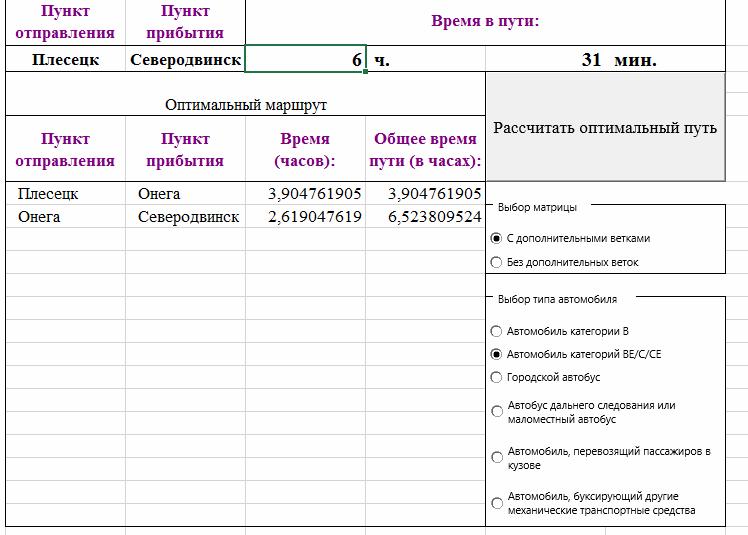
Результаты реализации разработанной модели транспортной инфраструктуры региона [5,6] с учетом новых проектов представлены на рисунке 3:
Рисунок 3 – Расчет времени в MS Excel для грузовиков с учетом дополнительных веток
Использование математических моделей, описанных в работе, на практике позволит проводить более детальный анализ и прогнозирование для принятия экономических решений.
Библиографический список
- Домнин Л.Н. Элементы теории графов: учеб. Пособие. Изд-во Пенз. Гос. Ун-та, 2007. – 144 с.
- Швецов В.И. Математическое моделирование транспортных потоков: Автоматика и телемеханика 2003.
- Гасников А.В., Кленов С.Л., Нурминский Е.А., Холодов Я.А., Шамрай Введение в математическое моделирование транспортных потоков: Учебное пособие / Под редакцией Гасникова А.В. – М.: МЦНМО, 2012.
- Урыков В.А., Зеленина Л.И. Математические модели транспортных потоков // Современная техника и технологии. 2015. № 6 [Электронный ресурс]. URL: http://technology.snauka.ru/2015/06/6051 (дата обращения: 17.06.2015).
- Зеленина Л.И., Урыков В.А. Моделирование транспортной инфраструктуры и развитие сельского хозяйства приарктических регионов // Сельское, лесное и водное хозяйство. 2015. № 6 [Электронный ресурс]. URL: http://agro.snauka.ru/2015/06/2461 (дата обращения: 02.07.2015).
- Зеленина Л.И., Урыков В.А. Моделирование транспортной инфраструктуры приарктических регионов // Исследования в области естественных наук. 2015. № 6 [Электронный ресурс]. URL: http://science.snauka.ru/2015/06/10204 (дата обращения: 01.07.2015).
Количество просмотров публикации: Please wait