В современном обществе все более востребованы креативные, творческие люди, умеющие самостоятельно разрешать сложные профессиональные и жизненные проблемы, находить нужную для этого информацию. Успешным становится человек, стремящийся совершенствовать свои способности, навыки, умения, не боящийся осваивать новые сферы деятельности, умеющий контактировать с другими людьми, сотрудничать с ними, реалистично оценивающий свои возможности и способный организовать себя для достижения намеченных целей. В этой связи, современная школа нацелена на формирование у учащихся познавательной потребности, умений самообучения, саморазвития, самоорганизации.
В последние годы в психологической и педагогической науке на первый план вышли технологии создания развивающей образовательной среды, стимулирующей самообучение и саморазвитие ребенка. Одним из перспективных направлений является реализация технологии продуктивного обучения в образовательной практике школьников.
Главная особенность продуктивного обучения – активизация процесса получения знаний на основе развития творческого мышления учащегося, развитие у него инициативности в организации своей познавательной деятельности.
Проблема развития творческого, креативного мышления начала разрабатываться учеными с середины XX века. Значительный вклад в исследование данной проблемы внес известный американский психолог Дж. Гилфорд, выявивший критерии креативности: оригинальность, гибкость, беглость и разработанность мышления, а также классифицировавший мышление на конвергентное и дивергентное.
Конвергентное мышление – это однонаправленное, последовательное, логическое мышление, играющее важную роль в формировании учебных действий ребенка.
Дивергентное мышление, в отличие от конвергентного, основано на поиске различных вариантов решений задачи и, соответственно, поиске многих вариантов правильных ответов. В раскрытии и развитии творческого потенциала ребенка роль задач дивергентного типа очень высока, поскольку их решение позволяет ему проявлять гибкость, беглость и оригинальность мышления.
В процессе изучения математики открываются большие возможности в развитии не только логического, абстрактного мышления, но и творческого, в частности, путем использования дивергентных задач.
Приведем примеры различных видов математических задач подобного типа.
1. Задачи комбинаторного характера
«В закрытой корзине лежат яблоки зеленого и красного цвета. Сколько яблок нужно достать из корзины не глядя, чтобы хотя бы два из них были одного цвета»?
Данная задача решается следующим образом. Достаем одно яблоко. Предположим, оно красного цвета. Достаем другое яблоко. Оно может быть либо красного, либо зеленого цвета. Если оно красное, то задача решена. Но гарантии, что оно красное, у нас нет – оно может быть зеленым. В этом случае придется достать еще одно яблоко. Тогда, какого бы цвета оно не было – красное или зеленое, у нас будет два яблока одного цвета. Таким образом, правильный ответ – три яблока.
Несмотря на то, что задача имеет единственный правильный ответ и единственно правильное объяснение этого ответа, она является дивергентной, поскольку, решая ее, ребенок должен сообразить, что их трех яблок будут либо все красные, либо все зеленые, либо два красных и одно зеленое, либо два зеленых и одно красное. В любом случае, будет два яблока одного цвета (не важно, какого).
2. Прогностические задачи
«Разделите квадрат на четыре равные части».
Варианты деления представлены на рисунке. Как правило, ребята легко находят первые три варианта, остальные три – не опираются на привычные, шаблонные решения.

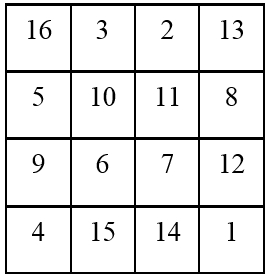
3. Задачи на магические квадраты
Магический квадрат представляет собой квадратную таблицу, заполненную целыми числами, причем сумма элементов любого столбца, любой строки, и любой из двух главных диагоналей одинакова. Пример магического квадрата представлен на рисунке.
Поскольку универсального способа заполнения магических квадратов не существует, данная задача относится к типу дивергентных.
4. Задачи на составление по заданному решению или уравнению
«Придумайте задачу по данной математической модели:
x = у
а = 2b
3c =2d
6т = 11n
5. Задачи, связанные с движением
«Из пунктов А и В, расстояние между которыми 30 км, выехали одновременно в противоположных направлениях два автомобиля, со скоростью 60 км в час каждый. Найти расстояние между автомобилями через один час после начала движения».
Из условия задачи видно, что данных для ее решения недостаточно, так как непонятно, удаляются ли автомобили друг от друга или сближаются. При решении следует предусмотреть оба варианта недостающего условия задачи. Соответственно, мы получаем два правильных ответа:
1) 60 + 60 + 30 = 150 (км)
2) 60 + 60 – 30 = 90 (км).
6. Задачи на построение и конструирование геометрических фигур
1) «Во что превращается окружность, если ее дорисовать другими геометрическими фигурами?»
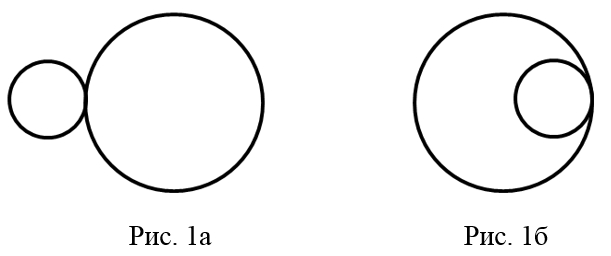
2) «Найти расстояние между центрами двух окружностей, радиусами 5 см и 2 см, касающимися друг друга».
В задаче неопределенность условия связана с тем, что не известно расположение окружностей относительно друг друга. В связи с этим, необходимо рассмотреть два варианта касания (рис. 1а; рис. 1б).
Мы рассмотрели лишь некоторые из возможных видов дивергентных задач. К этому типу относятся также задачи, связанные с разнообразием измерения величин; на состав и представление чисел; на общность признаков; на разработку версий причин событий; на преодоление инерции мышления; с недостающими данными, и др. Кроме того, в целях развития творческого мышления на уроках математики целесообразно использовать конвергентные задания, преобразовав их в дивергентные.
Библиографический список
- Бобылев Е.Л. Психология искусства Л.С. Выготского как общественная техника чувств // Высшее образование сегодня. – 2007. – № 11. – С. 69-70.
- Бобылев Е.Л. Проблема психологического анализа искусства в гуманитарной науке на стыке 19-20 веков // Приволжский научный вестник. – 2014. – № 11-2 (39). – С. 10-14.
- Трухманов В.Б. Компьютерная среда как средство формирования навыков анализа экономико-математических моделей // Приволжский научный вестник. – 2014. – № 3-2 (31). – С. 118-121.
- Трухманов В.Б. Компьютерные методы расчета регрессионных моделей в психологических задачах // Психология, социология и педагогика. – 2014. – № 7 (34). – С. 65-69.
- Трухманов В.Б., Трухманова Е.Н. Развитие дивергентного мышления школьников на уроках математики // Продуктивное образование: обобщение опыта экспериментальной работы: сборник научно-методических статей. – Арзамас: АГПИ, 2012. – С. 63-66.
- Трухманова Е.Н. Интернет-коммуникации как фактор социализации современных подростков и юношей // Приволжский научный вестник. – 2014. – № 11-2 (39). – С. 186-190.
- Трухманова Е.Н. Психолого-педагогические возможности развития интеллектуально-творческих способностей одаренных школьников // Психологическая наука в образовательном пространстве: матер. пятой регион. науч.-практ. конф. – Н.Новгород: НГПУ, 2008. – С. 156-159.
Количество просмотров публикации: Please wait