Процесс переработки серосодержащих газов, являющихся побочным продуктом многих производств, с рекуперацией элементарной серы по методу Клауса получил широкое применение в химической, нефтехимической и металлургической областях. Несмотря на широкое внедрение различных модификаций данного процесса и достаточно богатый накопленный опыт в проектировании и производстве установок Клауса, на данный момент в промышленных условиях поддерживать процесс на полном уровне конверсии по серосодержащим газам достаточно трудно. В результате неполной переработки реакционных газов, эффективность установки резко снижается. При этом происходит увеличение количества выбросов окислов серы в атмосферу. Окислы являются основным источником образования кислотных дождей, способных уничтожать сельскохозяйственные угодья, леса, поля, приводить к загрязнению земель и водоёмов, вызывая гибель речной фауны. Также выбросы оказывают негативное влияние организм человека и способны вызывать развитие следующих патологий: болезни системы кровообращения, нервной системы, органов дыхания и пищеварения. Для решения этой проблемы необходимо разработать математическую модель процесса рекуперации серы по двухступенчатому методу Клауса.
Математическое описание топки как технологического участка котла-утилизатора сводится к рассмотрению химически реагирующих потоков. Механизмы реакций, происходящих между компонентами потоков, в каждой точке пространстве и в каждый момент времени можно полностью описать через следующие параметры: давление, плотность, температуру, скорость потоков и концентрацию каждого из компонентов [1]. При этом необходимо учитывать, что составы исходных потоков и потока реакционной среды могут изменяться во времени [2].
Для описания процесса горения (окисления) сероводорода, метана и других составляющих потока реакционных газов составим систему уравнений сохранения массы и энергии. При составлении математического описания будем считать, что смесь топливо-воздух предварительно перемешана, а движение химически реагирующего потока ламинарно.
В общем случае уравнение материального баланса для ламинарного пламени можно записать в виде дифференциального уравнения первого порядка в частных производных [1]:
![]()
где: ![]() – массовая доля j компонента реакционной среды;
– массовая доля j компонента реакционной среды;
![]() – плотность реакционной среды;
– плотность реакционной среды;
![]() – средняя массовая скорость центра масс реакционной среды;
– средняя массовая скорость центра масс реакционной среды;
![]() – диффузионный поток j компонента реакционной среды;
– диффузионный поток j компонента реакционной среды;
![]() – массовая доля образования j компонента в химических реакциях. Уравнение материального баланса (1) описывает скорость изменения парциальных плотностей компонентов реакционной среды в результате образования или расходования компонентов реакционного потока и молекулярного переноса за счёт градиента концентраций реагентов.
– массовая доля образования j компонента в химических реакциях. Уравнение материального баланса (1) описывает скорость изменения парциальных плотностей компонентов реакционной среды в результате образования или расходования компонентов реакционного потока и молекулярного переноса за счёт градиента концентраций реагентов.
Для расчёта массовых долей продуктов реакционной среды с учётом влияния температуры горения и давления в топке котла-утилизатора на структуру цепочки химических превращений запишем уравнение минимальной свободной энергии Гиббса [3]:

где: ![]() – количество моль j компонента реакционной среды;
– количество моль j компонента реакционной среды;![]() – химический потенциал j компонента реакционной среды.В состоянии химического равновесия минимальная свободная энергия Гиббса достигает своего критического значения. Для нахождения количества моль каждого компонента реакционной среды в состоянии химического равновесия необходимо решить задачу нелинейного программирования. В качестве ограничений должны выполняться следующие выражения.
– химический потенциал j компонента реакционной среды.В состоянии химического равновесия минимальная свободная энергия Гиббса достигает своего критического значения. Для нахождения количества моль каждого компонента реакционной среды в состоянии химического равновесия необходимо решить задачу нелинейного программирования. В качестве ограничений должны выполняться следующие выражения.
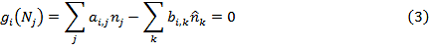
где: ![]() – количество атомов i элемента в j компоненте реакционной среды;
– количество атомов i элемента в j компоненте реакционной среды;![]() – количество атомов i элемента в k компоненте входного потока;
– количество атомов i элемента в k компоненте входного потока;
![]() – количество моль k компонента входного потока.На основании уравнений (2) и (3) составим скалярную функцию Гамильтона.
– количество моль k компонента входного потока.На основании уравнений (2) и (3) составим скалярную функцию Гамильтона.
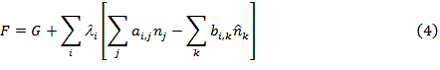
где: ![]() – множители Лагранжа.
– множители Лагранжа.
Для нахождения минимума функции Гамильтона (4) необходимо решить следующую систему уравнений.
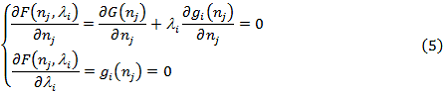
Преобразуем систему уравнений (5) к следующему виду.
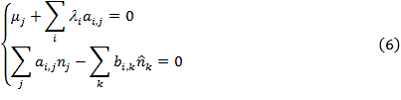
Химический потенциал j компонента реакционной среды можно определить по формуле [3].
где: ![]() – минимальная свободная энергия Гиббса при нормальных условиях;
– минимальная свободная энергия Гиббса при нормальных условиях;![]() – универсальная газовая постоянная;
– универсальная газовая постоянная;
![]() – температура реакционной среды;
– температура реакционной среды;
![]() – давление в топке котла-утилизатора;
– давление в топке котла-утилизатора;
![]() – давление при нормальных условиях;Подставим уравнение (7) в систему уравнений (6) и преобразуем к следующему виду.
– давление при нормальных условиях;Подставим уравнение (7) в систему уравнений (6) и преобразуем к следующему виду.
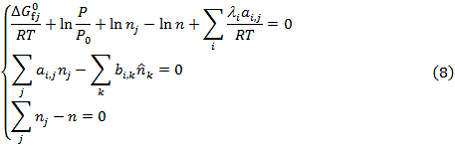
Составим уравнение сохранения энергии на основании уравнения сохранения энергии для ламинарного пламени [1] и уравнения теплового баланса проточного реактора идеального смешения [2]:
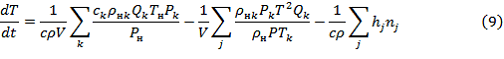
где: ![]() – удельная энтальпия j компонента реакционной среды;
– удельная энтальпия j компонента реакционной среды;
![]() – удельная теплоёмкость k компонента исходных потоков газов при постоянном давлении;
– удельная теплоёмкость k компонента исходных потоков газов при постоянном давлении;![]() – плотность k компонента исходных потоков газов при нормальных условиях;
– плотность k компонента исходных потоков газов при нормальных условиях;
![]() – объёмный расход k компонента исходных потоков газов;
– объёмный расход k компонента исходных потоков газов;
![]() – температура k компонента исходных потоков газов;
– температура k компонента исходных потоков газов;![]() – давление на линии подачи k компонента исходных потоков газов;
– давление на линии подачи k компонента исходных потоков газов;![]() – объём реактора.
– объём реактора.
Данное уравнение описывает изменение температуры реакционной среды во времени в зависимости от изменения параметров входных потоков: расходов и давлений в подводящих трубопроводах сероводорода, метана и воздуха.
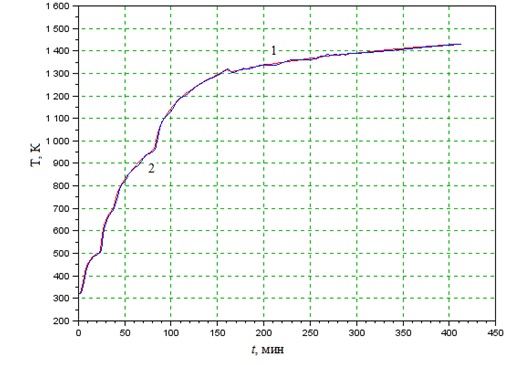
По экспериментальным данным, полученным при пуске котла-утилизатора 32Е 551 волжского завода органического синтеза, и на основании уравнений материального (8) и теплового (9) балансов проведём моделирование изменения температуры реакционной среды в топке котла-утилизатора (Рисунок 1).
Рисунок 1 – Изменение температуры реакционной среды в топке котла-утилизатора, 1 – экспериментальные данные, 2 – полученные по модели
Для анализа качества полученной математической модели определим относительную погрешность моделирования. На рисунке 2 представлен график изменения относительной погрешности моделирования температуры реакционной среды в топке котла-утилизатора.
Относительная погрешность имеет значительные выбросы только в течение первого запуска котла-утилизатора, вызванные низкой температурой реакционной среды и скачкообразным заданием расхода метана (Рисунок 2).
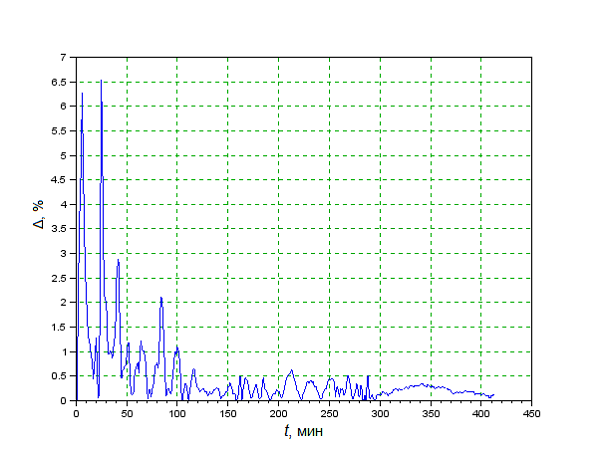
Рисунок 2 – Относительная погрешность моделирования изменения температуры реакционной среды в топке котла-утилизатора
Полученная математическая модель описывает изменение температуры реакционно среды в топке котла-утилизатора в зависимости от изменения расходов и состава поступающих газов. В таком виде математическая модель может быть использована в системе автоматического управления процессом рекуперации серы по двухступенчатому методу Клауса.
Библиографический список
- Варнатц Ю., Маас У., Диббл Р. Горение. Физические и химические аспекты, моделирование, эксперименты, образование загрязняющих веществ/ Пер. с англ. Г.Л. Агафонова. Под ред. П.А. Власова. – М.: ФИЗМАТЛИТ, 2003. – 352 с.
- Новый справочник химика и технолога. Процессы и аппараты химических технологий. Ч. II. – СПб.: НПО “Профессионал”, 2006. – 916 с., ил.
- Пригожин И., Кондепуди Д. Современная термодинамика. От тепловых двигателей до диссипативных структур: Пер. с англ. Ю.А. Данилова и В.В. Белого – М.: Мир, 2002. – 461 с., ил.
Количество просмотров публикации: Please wait