ВВЕДЕНИЕ
Как известно, «общая модель рыночной экономики представляет собой сложную иерархическую систему управления» [1]. Уровень технологического цикла труда есть первый уровень, в котором из предметов труда создаются продукты труда, причем, результаты труда на первом уровне (продукты труда с заданными свойствами) определяются вложенной энергией и управляющей информацией.
Как правило, экономика промышленного производства определяется результатами работы первого уровня управления – работой технологических циклов. «На первом уровне экономического управления создается весь ВВП, все общественное богатство».
«Второй уровень управления экономикой – координационный, производственный уровень, который объединяет различные циклы труда и координирует их деятельность в составе производства определенной продукции» [1].
Моделирование динамики изменения основных экономических показателей осуществляется, как правило, производственной функцией Кобба-Дугласа, описывающей трансформацию ресурсов в производственный результат (одна из разновидностей «неоклассической функции»), и моделью распределения валового продукта Кейнса.
Так, например, «чрезвычайно популярной в экономико-математическом моделировании является система, в которой активные элементы имеют функции затрат типа Кобба-Дугласа»[2,3,4]. Тем не менее, как утверждается в [5], «неоклассические функции являются лишь одним и не самым лучшим классом моделей», так как отражают неэффективное производство на участке убывающей ресурсоотдачи. От абстрактных экономических терминов капитал, сырье, труд производственных функций перейдем к конкретным понятиям изделие – оборудование. Важность такого подхода наиболее ярко проявляется в настоящее время в современной теории автоматического управления, в которой академиком А. А. Красовским [6] была поставлена проблема создания «физической теории управления», отличающейся от абстрактно-математической тем, что в физической теории управления модели и критерии создаются в физических величинах и терминах. Заложенные в математических моделях и критериях реальные факторы и ограничения должны фигурировать и в конечных результатах, определяя границы возможного и невозможного.
ОБЩАЯ ИДЕЯ МОДЕЛИ
Пусть участок дискретной производственной системы представляет собой [6] «закрытую систему А3 , не взаимодействующую со средой или другими системами и состоящую из двух открытых, или взаимодействующих (неизолированных), подсистем А1 (изделия) и А2 (оборудование). Для такой системы А3 необходимо учитывать принцип компенсации энтропии, который гласит, что «в неизолированной, а значит, во взаимодействующей системе энтропия одной системы может быть уменьшена только в том случае, если в процессе взаимодействия с другой или с другими системами происходит компенсирующее увеличение энтропии другой системы». Тогда для двух открытых и взаимодействующих подсистем А1 и А2, находящихся внутри изолированной (закрытой) системы А3 , выражение для изменения энтропии имеет вид ![]() , из которого следует, что если внутри изолированной системы А3 в одной подсистеме (например, А1 ) происходит снижение энтропии (
, из которого следует, что если внутри изолированной системы А3 в одной подсистеме (например, А1 ) происходит снижение энтропии (![]() ), то в другой (А2 ) энтропия должна на такую же величину возрасти (
), то в другой (А2 ) энтропия должна на такую же величину возрасти (![]() ),чтобы удовлетворялось условие
),чтобы удовлетворялось условие ![]() для общей изолированной системы А3. Итак, понижение энтропии в одной части изолированной системы и, следовательно, увеличение порядка требует обязательного повышения энтропии и, следовательно, увеличения беспорядка в другой части этой же системы, чтобы они компенсировали друг друга. Таким образом, если две (А1 и А2) или более открытые подсистемы взаимодействуют друг с другом и вместе составляют общую изолированную (закрытую) систему А3, то последняя остается равновесной, если величина изменения энтропии одной подсистемы будет равна изменению энтропии другой подсистемы, взятому с противоположным знаком».
для общей изолированной системы А3. Итак, понижение энтропии в одной части изолированной системы и, следовательно, увеличение порядка требует обязательного повышения энтропии и, следовательно, увеличения беспорядка в другой части этой же системы, чтобы они компенсировали друг друга. Таким образом, если две (А1 и А2) или более открытые подсистемы взаимодействуют друг с другом и вместе составляют общую изолированную (закрытую) систему А3, то последняя остается равновесной, если величина изменения энтропии одной подсистемы будет равна изменению энтропии другой подсистемы, взятому с противоположным знаком».
Рассмотрим один из простейших вариантов моделирования взаимодействия предметов труда с орудиями труда, учитывающей количество изделий, требующих обработки на входе системы, и количество и качество используемого на производственном участке оборудования.
МОДЕЛЬ УЧАСТКА УРОВНЯ ТЕХНОЛОГИЧЕСКОГО ЦИКЛА ТРУДА
Пусть в начальный момент времени t0 на производственном участке имеется: х0 – количество оборудования со средней производительностью α0 каждый; y0 – количество деталей на входе участка, которое необходимо обработать на данном оборудовании.
В общем случае за время Δt количество деталей на входе участка в результате обработки уменьшится на ![]() (дискретный вариант) или в непрерывном варианте скорость обработки (уменьшения) входного потока изделий определяется выражением:
(дискретный вариант) или в непрерывном варианте скорость обработки (уменьшения) входного потока изделий определяется выражением:
Чем больше оборудования на участке, чем выше его производительность, тем быстрее уменьшается входной поток деталей.
При обработке деталей (увеличение их порядка, определенности) происходит износ оборудования (увеличение беспорядка, хаоса) и производительность оборудования уменьшается пропорционально износу оборудования, поэтому будем считать ![]() . Причем, с учетом коэффициента износа оборудования k(y) получаем
. Причем, с учетом коэффициента износа оборудования k(y) получаем ![]() . Тогда уравнение (1) можно представить в виде:
. Тогда уравнение (1) можно представить в виде:
![]()
или после преобразования
![]()
В свою очередь, обработка деталей вызывает износ оборудования пропорциональный количеству обработанных деталей, причем обработка ymax деталей вызывает полный износ единицы оборудования, а одна деталь вызывает выбытие оборудования на величину ![]() . Учитывая, что скорость выбытия увеличивается с износом оборудования, можно записать скорость выбытия оборудования в зависимости от обработанных деталей
. Учитывая, что скорость выбытия увеличивается с износом оборудования, можно записать скорость выбытия оборудования в зависимости от обработанных деталей
Обработка изделий на участке осуществляется в течение времени технологического цикла (Тц ) для обрабатываемой партии деталей, календарный план обработки которых был предварительно рассчитан при подготовке производства. В качестве функции выхода участка примем количество обработанных деталей на выходе участка через указанное время Тц :
где ![]() .
.
Таким образом, модель производственной функции участка с учетом вышеприведенных уравнений можно представить следующим образом:
.gif) (4)
(4)где ![]() .
.
Простейшая модель технологического участка в виде системы уравнений (4) учитывает, таким образом, взаимовлияние оборудования на исходный массив деталей, а также монотонное постепенное понижение работоспособности оборудования вследствие износа в течение времени производственного цикла обработки изделий, что позволяет использовать модель для широкого класса производственных систем, где только обнаруживается такое взаимодействие.
РАСЧЕТ КОЭФФИЦИЕНТА ИЗНОСА ОБОРУДОВАНИЯ
В уравнении (4) используется коэффициент износа оборудования, зависящий от количества обработанных оборудованием деталей k(y). Вопрос моделирования закономерной динамики износа оборудования путем построения сглаженной кривой износа, показывающей связь между коэффициентом износа и хронологическим возрастом для каждой группы машин одного класса, изложен в [7,8].
Задача исследований оценщиков заключалась в том, чтобы разработать практические модели для обоснованного расчета сроков службы машин и оборудования, отталкиваясь от данных статистики о постепенном выбытии эксплуатируемых объектов при достижении определенного возраста.
Коэффициент износа, как отмечается в [7], есть величина, зависящая от времени и меняющаяся по следующей логистической кривой
где b - параметр, определяющий изгиб и положение линии относительно горизонтальной оси;
а – параметр наклона кривой в средней части;
kmax – максимальное значение коэффициента износа;
t – хронологический возраст оборудования.
В [7] отмечается, что начальное значение коэффициента износа может меняться следующим образом: ![]() , а максимальное значение при среднем износе работающего оборудования составляет приблизительно 0,9, а при старении оборудования без эксплуатации – 0,3.
, а максимальное значение при среднем износе работающего оборудования составляет приблизительно 0,9, а при старении оборудования без эксплуатации – 0,3.
Учитывая, что начальное значение коэффициента износа ![]() , можно найти значение b из выражения
, можно найти значение b из выражения ![]() .
.
Коэффициент а найдем из условия времени наработки на отказ заданного оборудования, при котором ![]() .
.
Таким образом, зная технические характеристики (наработку на отказ, предельный срок эксплуатации) указанного типа оборудования (Тотк ), при котором коэффициент износа оборудования равен 1, можно определить количество обработанных деталей данным типом оборудования за указанное время как ![]() , тогда
, тогда ![]() . В общем случае можно найти кривую износа станка в зависимости от количества произведенных деталей, т.е. от зависимости k(t) перейти к зависимости k(y).
. В общем случае можно найти кривую износа станка в зависимости от количества произведенных деталей, т.е. от зависимости k(t) перейти к зависимости k(y).
Выражение для коэффициента износа с учетом выражения (5) можно представить следующим образом:![]()
![]()
где y – количество обработанных деталей;
α – производительность оборудования.
Так, например, для ![]() ,
, ![]() , расчетном сроке службы оборудования 40000 часов, при производительности нового оборудования 5 изделий в час, выражение (6) будет выглядеть так:
, расчетном сроке службы оборудования 40000 часов, при производительности нового оборудования 5 изделий в час, выражение (6) будет выглядеть так:
Окончательно система уравнений (4), моделирующая производственный участок за время технологического цикла, может быть представлена следующим образом:
.gif) (8)
(8)где ![]() .
.
КАЧЕСТВЕННЫЙ АНАЛИЗ ПОВЕДЕНИЯ МОДЕЛИ
Огрубление модели (8) до модели Ланкастера с постоянными коэффициентами при x и y вида
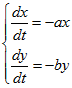 (9)
(9)позволяет нам получить точное решение такой жесткой модели,
«Эволюция x и y происходит вдоль гиперболы, заданной уравнением (10). Гиперболы разделены прямой ![]() . Топологический тип системы на плоскости (x, y) не меняется при изменении параметров a и b на функции a(x,y) и b(x,y) как в случае системы (8), а приводит лишь к искривлению центральной линии». Таким образом, в модели вида (8) нас будут интересовать только такие гиперболы, которые имеют начало ниже разделяющей гиперболы прямой. Только в этом случае гипербола выйдет на ось Х, а это значит, что все детали будут обработаны за конечное время.
. Топологический тип системы на плоскости (x, y) не меняется при изменении параметров a и b на функции a(x,y) и b(x,y) как в случае системы (8), а приводит лишь к искривлению центральной линии». Таким образом, в модели вида (8) нас будут интересовать только такие гиперболы, которые имеют начало ниже разделяющей гиперболы прямой. Только в этом случае гипербола выйдет на ось Х, а это значит, что все детали будут обработаны за конечное время.
ЧИСЛЕННЫЙ ЭКСПЕРИМЕНТАЛЬНЫЙ ПРИМЕР МОДЕЛИРОВАНИЯ ТЕХНОЛОГИЧЕСКОГО ЦИКЛА
Анализ искусственных модельных примеров в MATLAB Simulink расчета технологического цикла показал возможность использования предложенной математической модели (8) при конкретных значениях параметров системы:
Случай 1. Нормальный режим эксплуатации оборудования. Обработка y0 =2000 деталей на х0 =30 станках с начальной производительностью α0 =10 и коэффициентом износа оборудования как в (7). Фазовый портрет представлен на рис.1. Все детали обработаны за конечное время без потери качества. Как видно на рисунке, начало гиперболы (х0 , y0) фазового портрета расположено ниже разделяющей кривой.
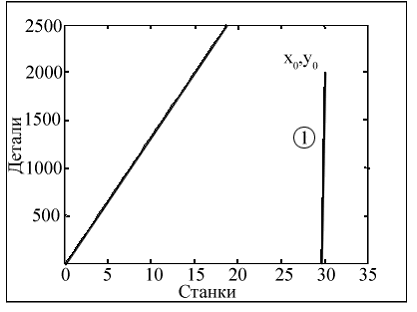
Рис.1. Фазовый портрет отмечен цифрой 1, случай первый
Случай 2. Катастрофическая загрузка оборудования. Обработка y0 =2000 деталей на меньшем количестве станков х0 =6 с начальной производительностью α0 =5 и коэффициентом износа оборудования как в (7) вызывает выбытие всего оборудования, что отражено на фазовом портрете для данного случая (рис.2). Детали не обработаны. Начало гиперболы фазового портрета расположено выше разделяющей кривой.
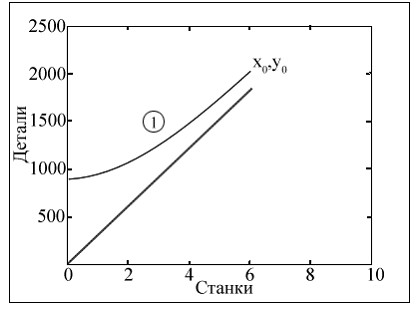
Рис.2. Фазовый портрет отмечен цифрой 1, случай 2
Изменение производительности оборудования влияет на кривизну гиперболы фазового портрета, что представлено на рисунках 3 и 4.
Случай 3. Обработка y0 =2000 деталей на х0 =7 станках с начальной производительностью α0 =5 вызывает напряженный режим обработки деталей, что отражено на фазовом портрете для данного случая (рис.3).
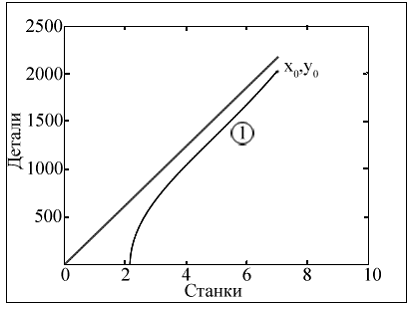
Рис.3. Фазовый портрет (отмечен цифрой 1) обработки y0 =2000 деталей на х0 =7 станках с начальной производительностью α0 =5
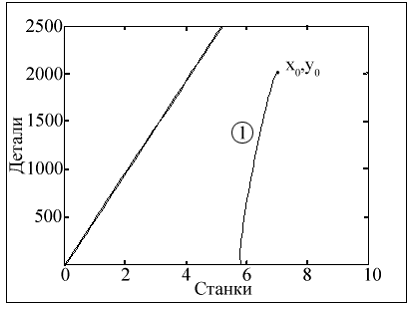
Рис.4. Фазовый портрет обработки y0 =2000 деталей на х0 =7 станках с начальной производительностью α0 =15.
ОСОБЕННОСТИ ФУНКЦИОНИРОВАНИЯ УЧАСТКА, МОДЕЛИРУЕМОГО ПРЕДСТАЛЕННОЙ СИСТЕМОЙ УРАВНЕНИЙ
Время моделирования работы технологического участка отличается от теоретического расчетного времени ввиду того, что теоретическое (начальное) значение производительности оборудования α0 меняется (уменьшается) в результате эксплуатации оборудования. Модельное время технологического цикла tм больше, чем расчетное теоретическое время tр :
Интересные закономерности проявляются при моделировании производственного участка, имеющего оборудование одинаковой надежности, но разной производительности, причем общая производительность заданного количества оборудования (производительность участка) одинаковая, т.е. ![]() .
.
Зависимость обработки заданного количества деталей y0 =2000 при разном количестве оборудования х0 представлена на рис.5., при этом ![]() , т.е. производительность единицы оборудования при росте х уменьшается пропорционально, но производительность участка остается постоянной. Как видно из графика, выполнение плана гарантируется только начиная с 10 станков и более, что не является очевидным фактом, ведь общая производительность участка не меняется. При этом, как представлено на рис.6., при гарантированном выполнении плана время технологического цикла уменьшается с ростом количества станков, что очевидно.
, т.е. производительность единицы оборудования при росте х уменьшается пропорционально, но производительность участка остается постоянной. Как видно из графика, выполнение плана гарантируется только начиная с 10 станков и более, что не является очевидным фактом, ведь общая производительность участка не меняется. При этом, как представлено на рис.6., при гарантированном выполнении плана время технологического цикла уменьшается с ростом количества станков, что очевидно.
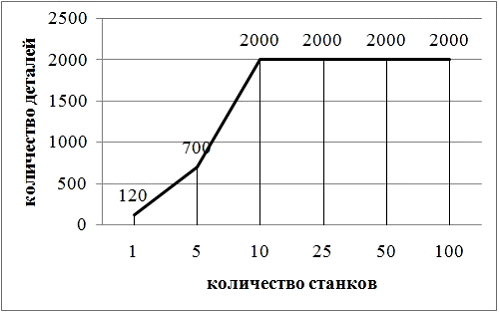
Рис.5. Зависимость выполнения плана y0 по обработке заданного количества деталей от количества станков при постоянной производительности участка.
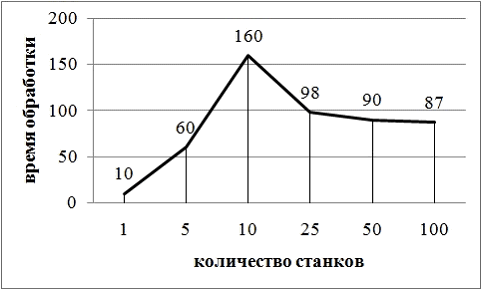
Рис.6. Зависимость времени обработки партии деталей от количества станков.
ЗАКЛЮЧЕНИЕ
Предложенная нелинейная модель участка дискретной производственной системы в виде системы уравнений (8) учитывает такие физические величины как количество и актуальное на данный момент текущее качество оборудования (станков), время технологического цикла, количество деталей. Предварительный анализ положения начальных значений гиперболы относительно разделяющей кривой позволяет определить устойчивость процесса обработки. Анализ модели показал, что при заданной общей производительности участка целесообразно использовать большее количество оборудования с низкой производительностью, чем меньшее количество с более высокой производительностью при условии, что минимизируется общее время выполнения технологического цикла (время обработки всего массива изделий). Таким образом, относительно простая нелинейная модель позволяет моделировать функционирование дискретной производственной системы с целью: управления участком по выпуску изделий, замены и ремонта оборудования участка, расчета необходимого количества станков с заданными свойствами для обработки необходимого объема деталей, расчета объема партии деталей для обработки на заданном количестве станков с известными характеристиками и т. д., что делает ее достаточно актуальной при моделирование дискретных производств. Существует возможность использования модели для любых типов производства.
Библиографический список
- Демин А.И. Информационная теория экономики. Макромодель.2-е изд., стер., КомКнига, ЛКИ, 2007. – 352 с.
- Бурков В.Н., Новиков Д.А. Теория активных систем: Состояние и перспективы.М.:Синтег, 1999.-128 с.
- Новиков Д.А., Петраков С.Н. Курс теории активных систем. М.:Синтег, 1999.-104 с.
- Новиков Д.А. Математические модели формирования и функционирования команд. - М.: Издательство физико-математической литературы, 2008.-184 с.
- Светуньков С.Г. Моделирование инновационной динамики // Инновации, конкуренция и предпринимательство/ Под ред. С. Г. Светунькова.- СПб.: Изд-во СПбГУЭФ, 2008.-С.18-34.
- Синергетика и проблемы теории управления / Под ред. А. А. Колесникова. – М.: ФИЗМАТЛИТ, 2004. – 504 с.
- http://www.labrate.ru/teveleva/teveleva_article_ocenka_oborud_2007-1.htm
- Тевелева О.В. Вопросы исследования показателя фондоотдачи от активной и пассивной части основных фондов // «Актуальные проблемы управления-2006», Вып.4.-М.:ГУУ, 2006.- с.190-194.
Количество просмотров публикации: Please wait


