Современный уровень развития машин, механизмов, летательных аппаратов, требует от строительной механики использования в расчетах движения ускорений высших порядков. Напомним, что собственно «ускорение» – вектор, характеризующий быстроту изменения скорости по величине и направлению [1-4]. Понятие рывка, связанного с третьей производной по координате, используется, например, в прямых методах решения задач динамики[5-12] – методе линейного ускорения. В этом методе на каждом шаге по времени предполагается, что ускорение изменяется линейно, т.е. на каждом шаге рывок постоянный.
Рывок называется ускорением 2-го порядка. Основные понятия и кинематические теоремы ускорений высших порядков были сформулированы Резалем и Сомовым в 1862 – 1866 г.г. В настоящее время большое значение приобретают динамические аспекты использования ускорений высших порядков в теории сейсмостойкости и исследовании колебаний зданий.
В данной работе предполагается компактный вывод формулы рывка в естественных координатах. При этом используются уравнения дифференциальной геометрии – формулы Френе.
Примем следующие обозначения: ![]() - единичные векторы, направленные по осям естественного трехгранника,
- единичные векторы, направленные по осям естественного трехгранника, ![]() - кривизна траектории, χ – кручение траектории,
- кривизна траектории, χ – кручение траектории, ![]() - радиус кривизны, T– радиус кручения,
- радиус кривизны, T– радиус кручения, ![]() - скорость точки, S – дуговая координата,
- скорость точки, S – дуговая координата, ![]() - рывок.
- рывок.
Выражение для ускорения в естественных координатах имеет вид:
![]() . (1)
. (1)
Дифференцируя уравнение (1) по времени получим:
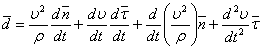 . (2)
. (2)
Для упрощения этого уравнения используем формулы Френе:
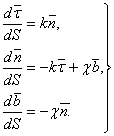 . (3)
. (3)
и переходные формулы вида:
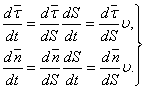 . (4)
. (4)
В результате несложных преобразований:
.gif)
мы получаем формулу рывка или ускорения второго порядка в естественных координатах:
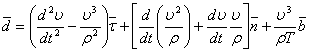 . (5)
. (5)
Дифференцируем уравнение (5) по времени по частям:
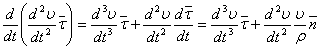 . (6)
. (6)
.gif) . (7)
. (7)
.gif) . (8)
. (8)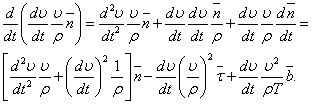 (9)
(9)
.gif) . (10)
. (10)
Подставляем уравнения (6) – (10) в уравнение (5) и получаем формулу ускорения третьего порядка:
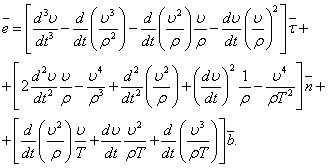 (11)
(11)Библиографический список
- Никитин Н.Н. КУРС ТЕОРЕТИЧЕСКОЙ МЕХАНИКИ. М., Высшая школа, 1990.-607 с.
- Кононенко Т.И. К ТЕОРИИ УСКОРЕНИЙ ВЫСШИХ ПОРЯДКОВ. Теоретическая механика. Сборник научно-методических статей №7, м., Высшая школа,1976.
- Воднев В.Т. и др. ОСНОВНЫЕ МАТЕМАТИЧЕСКИЕ ФОРМУЛЫ. М., Высшая школа, 1980.-336с.
- Шеин А.И. КРАТКИЙ КУРС ТЕОРЕТИЧЕСКОЙ МЕХАНИКИ. Пенза, ПГУАС, 2005.-224с.
- Шеин А.И. РЕШЕНИЕ МНОГОПАРАМЕТРИЧЕСКОЙ ЗАДАЧИ ДННАМИКИ СТЕРЖНЕВЫХ СИСТЕМ МЕТОДОМ СЕТОЧНОЙ АППРОКСИМАЦИИ ЭЛЕМЕНТОВ
Промышленное и гражданское строительство. 2002. № 2. С. 27. - Шеин А.И., Зайцев М.Б. МЕТОД СМЕЩЕННЫХ РАЗНОСТЕЙ ДЛЯ РЕШЕНИЯ СИСТЕМ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ДВИЖЕНИЯ МЕХАНИЧЕСКИХ СИСТЕМ
Строительная механика и расчет сооружений. 2012. № 2. С. 38-41. - Шеин А.И., Бакушев С.В. , Зайцев М.Б., Земцова О.Г. ГАШЕНИЕ КОЛЕБАНИЙ ВЫСОТНЫХ СООРУЖЕНИЙ
в 3 ч. / А. И. Шеин [и др.] ; М-во образования и науки Российской Федерации, Гос. образовательное учреждение высш. проф. образования “Пензенский гос. ун-т архитектуры и стр-ва”. Пенза, 2011. - Шеин А.И., Шмелев Д.А. ОЦЕНКА ЭФФЕКТИВНОСТИ АКТИВНОГО ЖИДКОСТНОГО ГАСИТЕЛЯ КОЛЕБАНИЙ ВЫСОТНЫХ СООРУЖЕНИЙ ПРИ НЕСТАЦИОНАРНЫХ ВОЗДЕЙСТВИЯХ
Строительная механика и расчет сооружений. 2014. № 1 (252). С. 59-63. - Шеин А.И., Земцова О.Г. СХЕМЫ И ТЕОРИЯ ГАСИТЕЛЕЙ ПРОСТРАНСТВЕННЫХ КОЛЕБАНИЙ СООРУЖЕНИЙ
Региональная архитектура и строительство. 2010. № 1. С. 45-52. - Шеин А.И., Земцова О.Г. СНИЖЕНИЕ УРОВНЯ КОЛЕБАНИЙ СИСТЕМЫ «УПРУГОЕ ОСНОВАНИЕ – ВЫСОТНОЕ СООРУЖЕНИЕ» С ПОМОЩЬЮ НЕЛИНЕЙНОГО ДИНАМИЧЕСКОГО ГАСИТЕЛЯ
Региональная архитектура и строительство. 2011. № 2. С. 83-90. - Шеин А.И., Земцова О.Г. ОПТИМИЗАЦИЯ МНОГОМАССОВЫХ ГАСИТЕЛЕЙ КОЛЕБАНИЙ ПРИ ГАРМОНИЧЕСКОМ ВОЗДЕЙСТВИИ
Известия высших учебных заведений. Поволжский регион. Технические науки. 2010.№ 1. С. 113-122. - Шеин А.И., Шмелёв Д.А. ПОСТРОЕНИЕ И РЕАЛИЗАЦИЯ МАТЕМАТИЧЕСКОЙ МОДЕЛИ ГАШЕНИЯ КОЛЕБАНИЙ ВЫСОТНЫХ ЗДАНИЙ С ПОМОЩЬЮ РЕАКТИВНЫХ ГАСИТЕЛЕЙ
Региональная архитектура и строительство. 2014. № 1. С. 96-103.
Количество просмотров публикации: Please wait


