Введение
В работе рассматривается связанное состояние электрона и позитрона- Позитроний. Путем решения нового релятивистского уравнения М2 [1] показано, что кроме известных водородоподобных состояний, Позитроний имеет устойчивые компактные состояния с высокой энергией связи.
Полученные состояния могут быть интерпретированы как частицы и элементарные ячейки структуры физического вакуума.
Данную статью можно скачать в формате PDF по ссылке - https://portalnp.snauka.ru/wp-content/uploads/2015/02/Positronium.pdf
Радиальное уравнение М2 для Позитрония
Поскольку масса позитрона равна массе электрона, то уравнение для Позитрония будет отличатся от уравнения для атома водорода заменой массы ![]() на приведенную массу
на приведенную массу ![]() . Запишем радиальное уравнение М2 для Позитрония:
. Запишем радиальное уравнение М2 для Позитрония:
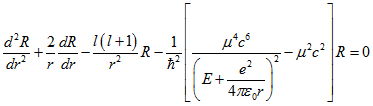 (1.1)
(1.1)
Далее будем применять атомную систему единиц Хартри. Перепишем уравнение (1.1) в атомных единицах Хартри ![]() .
.
С учетом значения приведенной массы ![]() уравнение (1.1) в атомных единицах Хартри примет вид:
уравнение (1.1) в атомных единицах Хартри примет вид:
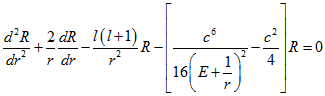 (1.2)
(1.2)
Для решения полученного уравнения, воспользуемся математическим интернет ресурсом WolframAlpha http://www.wolframalpha.com/
Решение для радиальной волновой функции имеет следующий вид:
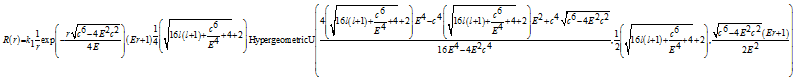 где
где ![]() вырожденная гипергеометрическая функция второго рода,
вырожденная гипергеометрическая функция второго рода, ![]() константа интегрирования.
константа интегрирования.
Как известно, первый параметр вырожденной гипергеометрической функции является радиальным квантовым числом со знаком минус ![]() .
.
Из этих соображений, получаем уравнение для определения энергии основного состояния и возбужденных состояний Позитрония в следующем виде:
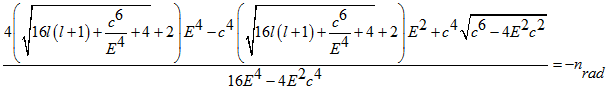 (1.3)
(1.3)
Определим энергии Позитрония для основного состояния ![]() и первого возбужденного состояния с обитальным моментом
и первого возбужденного состояния с обитальным моментом ![]() .
.
Решая уравнение (1.3) с параметрами ![]() получим:
получим: ![]() .Далее будем анализировать только положительные значения энергии полученных при решении уравнения. Хотя уравнение дает симметричные решения. Однако, в графических представлениях приведем полную картину для наглядности.
.Далее будем анализировать только положительные значения энергии полученных при решении уравнения. Хотя уравнение дает симметричные решения. Однако, в графических представлениях приведем полную картину для наглядности.
Полученная энергия включает в себя энергию покоя. Учитывая это и переведя значение энергии из атомных единиц Хартри в электронвольты получим: ![]() . Полученная энергия является энергией основного состояния
. Полученная энергия является энергией основного состояния ![]() .
.
Теперь определим энергию первого возбужденного состояния![]() .
. ![]() .
.
Построим график зависимости энергии от радиального квантового числа для сферически симметричных состояний с орбитальным моментом ![]() согласно уравнению (1.3) Рис.1.
согласно уравнению (1.3) Рис.1.
На графике точка 1 соответствует основному состоянию ![]() . Точка 2 соответствует первому возбужденному состоянию
. Точка 2 соответствует первому возбужденному состоянию ![]() . Состояния 3 и 4 будут анализированы позже.
. Состояния 3 и 4 будут анализированы позже.
Приведем график нормированной радиальной плотности вероятности для основного состояния и первого возбужденного состояния Рис.2.
Полученные значения энергий и приведенные графики доказывают, что уравнение М2 вполне адекватно описывает атом Позитрония.
Убедившись в этом перейдем к рассмотрению более экзотических состояний Позитрония вытекающих из решения уравнения М2. Эти решения не имеют аналогов для других уравнений квантовой механики и являются специфическими для уравнения М2.
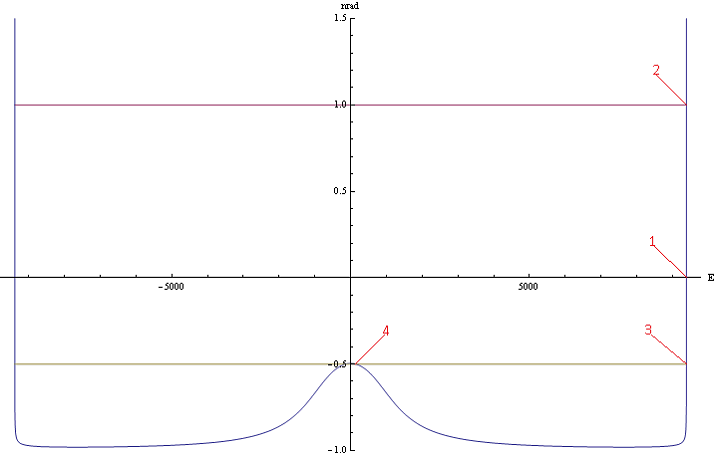
Рис.1 График зависимости энергии от радиального квантового числа ![]() при
при ![]()
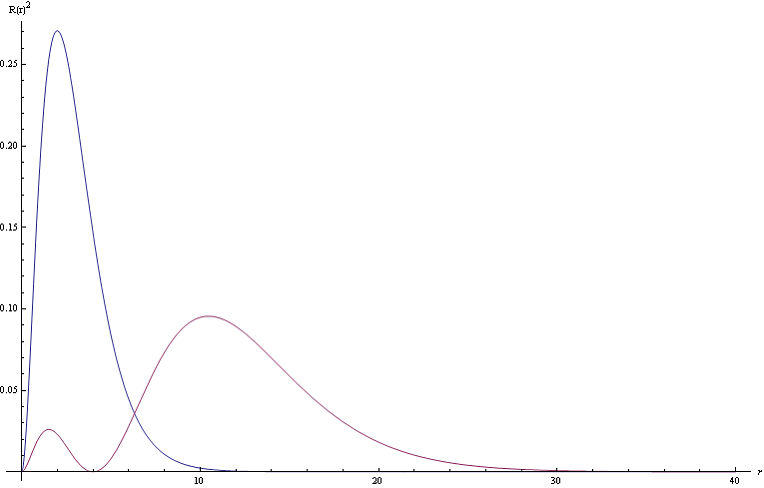
Рис.2 Нормированная радиальная плотность вероятности основного состояния и первого возбужденного состояния в атомных единицах Хартри.
Экзотические, сильно локализованные, компактные состояния Позитрония
Предположение о существовании компактных локализованных состояний Позитрония, предполагает наличие высокой энергии связи. Энергия связи должна быть выше чем принятого основного состояния. А это в свою очередь предполагает смещение радиального квантового числа в сторону отрицательных значений ![]() . Посмотрев на график зависимости энергии от квантового числа Рис.1. можно понять, что таким значением является
. Посмотрев на график зависимости энергии от квантового числа Рис.1. можно понять, что таким значением является ![]() .
.
Впервые в практику решений квантово-механических уравнений введем новое значение радиального квантового числа ![]() . Вследствие этого, возникают два новых состояния 3 и 4.
. Вследствие этого, возникают два новых состояния 3 и 4.
Поскольку нас интересуют сильно связанные компактные состояния, то пока состояние 3 анализировать не будем. Этим условиям удовлетворяет состояние 4.
Пользуясь уравнением (1.3) определим энегию этого состояния для случая ![]() . Решение дает:
. Решение дает: .gif) подставляя в полученную формулу значение скорости света
подставляя в полученную формулу значение скорости света ![]() получим энергию
получим энергию ![]() в атомных единицах Хартри. В электронвольтах энергия будет имеь значение:
в атомных единицах Хартри. В электронвольтах энергия будет имеь значение: ![]() . Таким образом мы получили энергию основного состояния из серий сильно локализованных состояний. Фиксируя значение радиального квантового числа на значении
. Таким образом мы получили энергию основного состояния из серий сильно локализованных состояний. Фиксируя значение радиального квантового числа на значении ![]() , можно, решая уравнение (1.3), получить универсальную формулу связи энергии и орбитального квантового числа
, можно, решая уравнение (1.3), получить универсальную формулу связи энергии и орбитального квантового числа ![]() . Тем самым можно определить энергии возбужденных состоянии по орбитальному моменту при фиксированном значении радиального квантового числа
. Тем самым можно определить энергии возбужденных состоянии по орбитальному моменту при фиксированном значении радиального квантового числа ![]() .
.
Формула взаимосвязи энергии и орбитального квантового числа будет иметь следующий вид:
.gif) (2.1)
(2.1)
На Рис.3. приведены значения энергии компактного позитрония вычисленные по формуле (2.1) для состояний радиального квантового числа ![]() и орбитального квантового числа
и орбитального квантового числа ![]()
Приведем в графическом виде поведение энергии в окресности состояния 4 Рис.1 для различных значений орбитального квантового числа. Рис.4.
Рассматривая полученные решения и графики, можно придти к неожиданному заключению. А именно: при компактных состояниях Позитрония, возбуждение по орбитальному моменту приводит к снижению энергии. То есть основное состояние имеет энергию выше чем последующие возбужденные состояния.
В случае рассмотрения компактного состояния Позитрония в качестве элементарной ячейки структуры вакуума, это будет означать, что основное состояние вакуума имеет ненулевую энергию. Более того, возбужденные состояния вакуума имеют энергию ниже чем основное состояние. Только в предельно возбужденном состоянии энергия вакуума стремится к нулю.
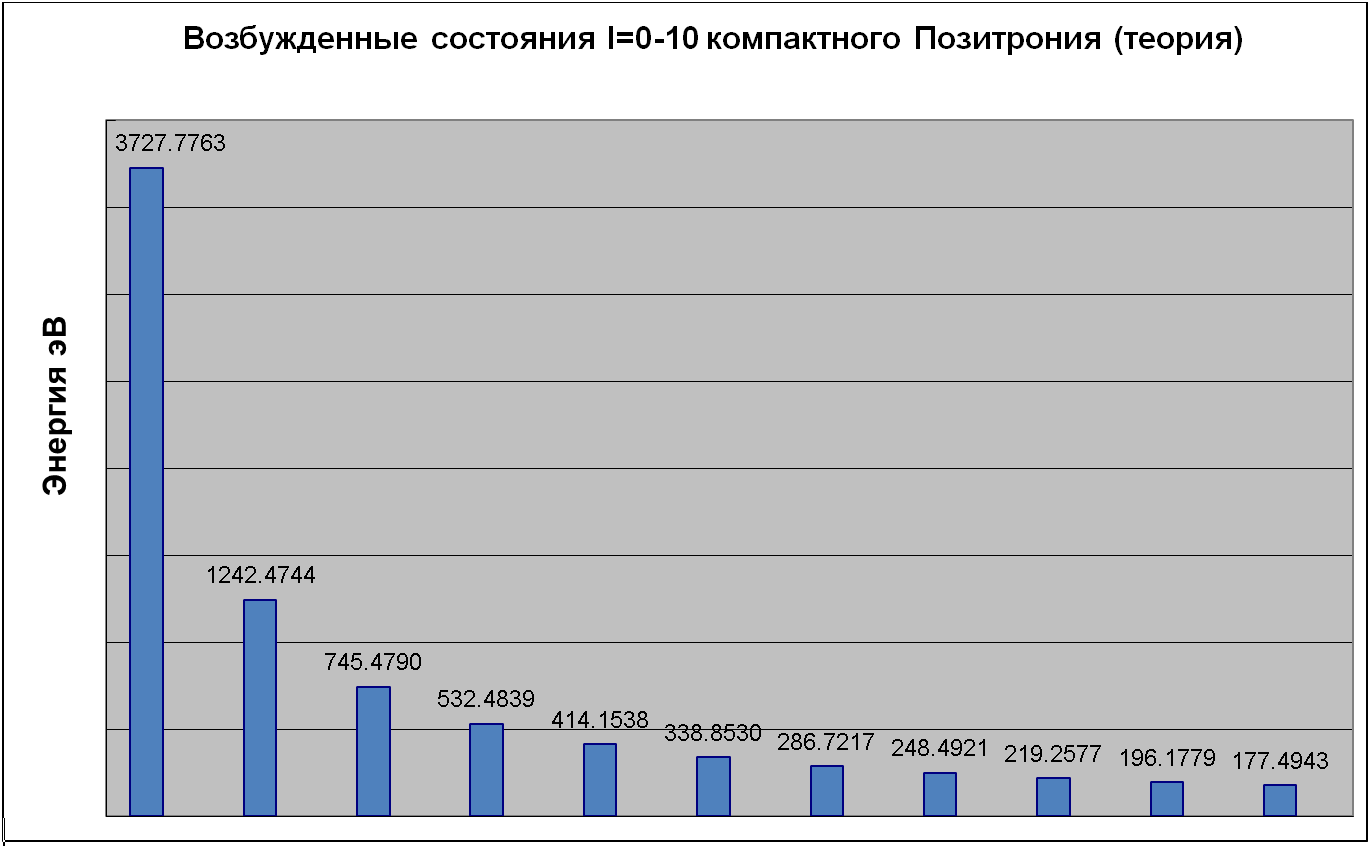
Рис.3. Значения энергии компактного позитрония вычисленные по формуле (2.1) для состояний радиального квантового числа ![]() и орбитального квантового числа
и орбитального квантового числа ![]() .
.
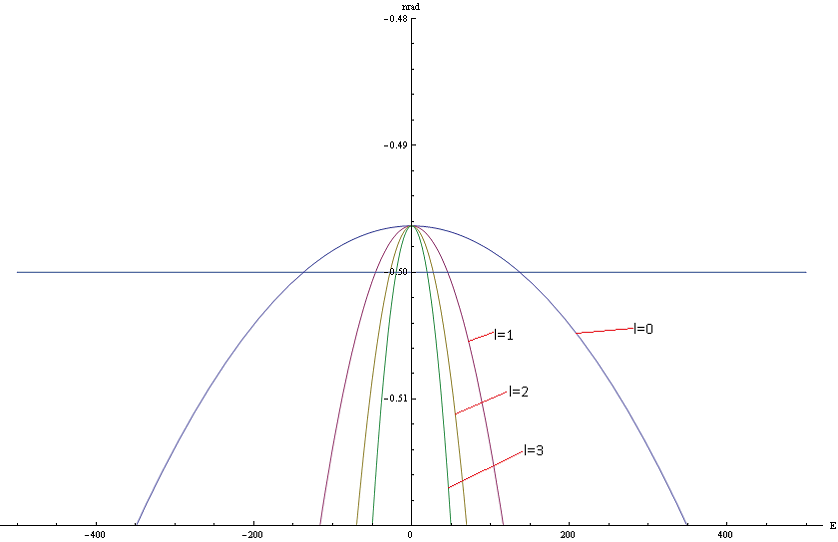
Рис.4. Графики энергии при различных значений орбитального квантового числа ![]()
Приведем график радиальной плотности вероятности основного состояния ![]() компактного Позитрония Рис.5.
компактного Позитрония Рис.5.
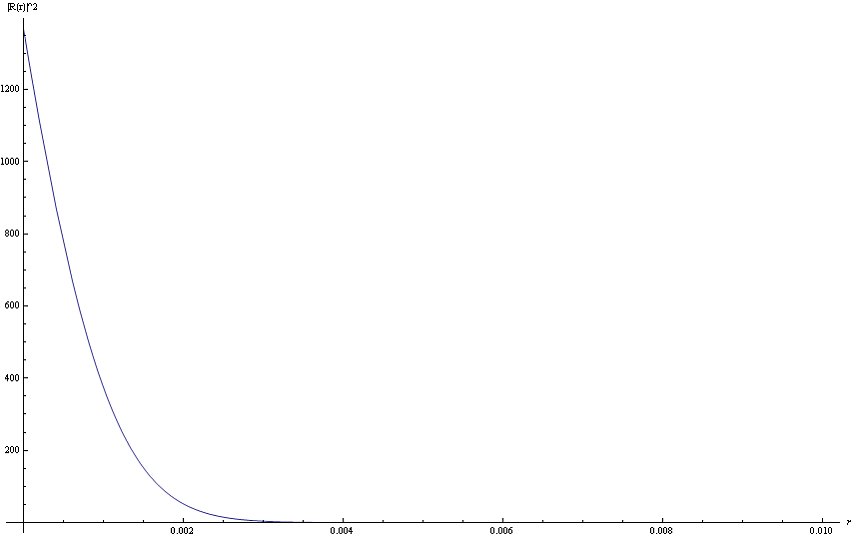
Рис.5. Нормированная радиальная плотность вероятности основного состояния ![]() компактного Позитрония, в атомных единицах Хартри.
компактного Позитрония, в атомных единицах Хартри.
Результаты и обсуждения
Теоретические и экспериментальные данные о наличии в вакууме квантованных энергетических уровней, находим в работах академика Р.Авраменко и его сотрудников из НИИ Радиоприборостроения [2].
Ими была получена новая константа: ![]() характеризующая ненулевую энергию элементарной ячейки вакуума. По терминологии автора “Специфическая квантовая энергия”.
характеризующая ненулевую энергию элементарной ячейки вакуума. По терминологии автора “Специфическая квантовая энергия”.
Далее автор приводит экспериментальное подтверждение наличия в вакууме константы ![]() . В описанном эксперименте наблюдается резонансный характер эмиссии электронов в вакуум при достижении напряжения
. В описанном эксперименте наблюдается резонансный характер эмиссии электронов в вакуум при достижении напряжения ![]() .
.
Второе подтверждение существования константы ![]() находим в работе [3] Холодов Л.И., Горячев И.В. “О свойствах лептонной квадриги Терлецкого в электромагнитном вакууме”.
находим в работе [3] Холодов Л.И., Горячев И.В. “О свойствах лептонной квадриги Терлецкого в электромагнитном вакууме”.
В работе также предпринята попытка описания “Иерархии” качественно различных уровней материи.
А в настоящей работе, та же самая константа получена, при решении уравнения М2 для компактного, связанного состояния Позитрония. Кроме того показано, что возбужденные состояния вакуума имеют более низкую энергию чем основное состояние. А это прямая возможность доступа к неисчерпаемому и чистому источнику энергии.
Получение одного и того же значения тремя независимыми исследованиями и различными методиками, не может быть случайным. Это доказывает, что в вакууме существуют квантованные состояния с определенными значениями энергии. А основное состояние ячейки структуры вакуума имеет энергию ![]() .
.
Библиографический список
- Дангян А.Э. “Новое уравнение релятивистской квантовой механики”
- Будущее открывается квантовым ключом. Сб. статей академика Р.Ф.Авраменко.–М., «Химия», 2000.
- Холодов Л.И., Горячев И.В. “О свойствах лептонной квадриги Терлецкого в электромагнитном вакууме”.
Количество просмотров публикации: Please wait


