Качество изделий машиностроения – категория комплексная, и его важнейшим показателем является надежность, включающая в себя безотказность, долговечность, ремонтопригодность и сохраняемость, а также точность, прочность, износостойкость и др., в зависимости от назначения изделия [1].
Рассмотрим оценку надежности изделий на примере валов малой жесткости (ВМЖ) оборудования легкой промышленности.
Ответственными элементами технологического оборудования текстильной отрасли машиностроения, определяющими эффективность его эксплуатации, являются валы малой жесткости.
О жесткости вала судят по отношению его длины (l) к диаметру (d): , где k = 3…5 – жесткие валы, k = 5…10 – валы средней жесткости, k = 10…12 и более – маложесткие.
Валы имеют сплошное круглое сечение и кольцевое. К ним относятся вытяжные цилиндры, мотальные, плющильные и другие валы прядильного оборудования. Их количество на одну прядильную машину составляет до 170 единиц. Опыт эксплуатации и анализ отказов технологического оборудования прядильных производств показывает, что до 30 % отказов по количеству и до 60 % по времени простоя приходится на валы малой жесткости. Замена вышедших из строя ВМЖ связана с демонтажем линии валов, а также сопрягаемых узлов и деталей, с полной или частичной потерей работоспособности оборудования [2].
Линия ВМЖ состоит из ряда звеньев, имеет протяженность от 1,5 до 16 м, является многоопорным многозвенным валом. Замена вышедшего из строя одного из звеньев связана с остановом ленточных машин или с отключением одной стороны прядильных машин; с полной или частичной потерей работоспособности, с демонтажом линии валов и сопрягаемых узлов и деталей. Поэтому время простоя машин для замены двух и более валов составляет не менее 8 ч.
Прогнозирование долговечности ВМЖ необходимо для обеспечения работоспособного состояния технологического оборудования и определения закономерности изменения работоспособности в процессе работы.
Для оценки надежности изделий используются качественные и количественные показатели. Качественные показатели не выражены в численном значении, не содержат информации, позволяющей обосновать предпочтение, например одной модификации ВМЖ другой при сравнении их качества. Качественные показатели дают возможность отличить один вал от другого, например, по внешнему виду, конструктивному оформлению цапфы. К качественным показателям относятся также и порядковые или экспертные оценки, которые дают возможность расположить исследуемые валы в ряд по степени точности, шероховатости, сопротивления усталости и др. 1.
Количественные показатели надежности содержат информацию, позволяющую провести сравнительную оценку, выражаются в виде числовых характеристик в абсолютных или относительных единицах, они могут быть получены из статистических данных на основе обработки результатов с использованием теории вероятности и математической статистики, а также путем аналитических расчетов или физического моделирования и испытаний на реальных машинах или стендах, имитирующих условия эксплуатации или ускоренные испытания.
В качестве основного свойства надежности отдельного звена вала можно выделить долговечность. Долговечность – это свойство ВМЖ сохранять работоспособное состояние до наступления предельного состояния. Предельное состояние валов характеризуют следующие виды отказов: повреждение хромового покрытия, усталостное разрушение вала, искривление оси и биение вала выше допустимого, неразвинчиваемость линии на звенья из-за повреждения фреттинг-коррозией. Согласно ГОСТ Р 27.002-2009 в качестве оценочных показатели долговечности могут быть выбраны: средний срок службы или -процентный ресурс.
При выборе показателей долговечности ВМЖ главным критерием является экономическая и практическая целесообразность. Таким показателем ВМЖ может быть средний срок службы, так как машины работают, как правило, непрерывно в трехсменном режиме. 
Точку зрения на проблему способов оценки долговечности изнашиваемых деталей, в том числе ВМЖ, можно подразделить на две основные категории: полное отсутствие какой-либо информации (весьма редкий случай) и наличие статистических данных. В первом случае (касается ответственных деталей и узлов) количественную оценку получают аналитическим путем, либо испытаниями модельных систем или опытных образцов. Аналитический метод базируется, например, на сопоставлении данных эксплуатации прототипа. При отсутствии статистики по эксплуатации валов – единственный путь прогнозирования показателей долговечности состоит в проведении испытаний представительной выборки специально изготовленных валов по выбранной технологии на усталость.
Во многих методиках для расчета средних сроков службы обоснования используют экспоненциональное распределение.
Проектируемый срок службы Т_П валов (в годах) не должен быть меньше моральной долговечности машин, который может быть определен по формуле [3]:

,

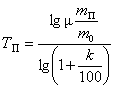где – коэффициент, принимается равным 1,5…1,6 или рассчитывается по методике [4]; m₀ – техническая норма физической долговечности рассматриваемого срока службы до среднего ремонта – 4 мес.; m_П – срок службы для проектируемого оборудования;  – прирост производительности машин. Прирост производительности вновь проектируемой или модернизируемой ленточной машины составляет 25 %, тогда ; k средний годовой прирост производительности труда, в текстильной отрасли k = 6 %. 
Тогда Т_П примет значения

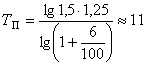 лет.

Фактически машины эксплуатируются 20 и более лет.
Известно, что чаще фактические сроки службы (ресурсы) изнашиваемых деталей распределены по законам: нормальному, логарифмически-нормальному, Вейбулла [3].
При расчете использованы данные эксплуатационной статистики, полученные на текстильных предприятиях городов Санкт-Петербурга, Иванова, Москвы и др.
Установлено, что распределение сроков службы и ресурса деталей машин, в том числе и валов, описываются двухпараметрическими законами с плотностью вероятностей для законов:
▪ нормального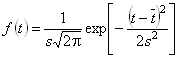 

где  плотность распределения сроков службы;  средний срок службы; s – среднее квадратическое отклонение (стандартная ошибка);
▪ логарифмически нормального

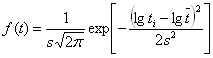
▪ закона Вейбулла (закон трехпараметрический)

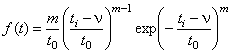
0; m 0, где – параметр положения кривых распределения, любое действительное число в единицах случайной величины. Для валов явные отказы в начальный период эксплуатации весьма редки, поэтому можно принять = 0 и привести функцию распределения к виду

,

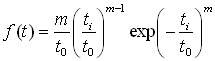где t_i – количественный признак случайной величины, который принимает значения t₁, t₂…t_nk, соответствующие действительным срокам службы деталей в календарных единицах времени (месяцах); t₀ – параметр масштаба кривой распределения; m – параметр формы кривой.
Параметр распределения Вейбулла m однозначно связан с коэффициентом вариации сроков службы уравнением:

,

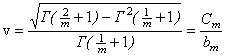где ; ; – гамма-функция аргумента t. Коэффициенты b_m и С_m зависят только от параметра m, значения их табулированы в зависимости от m, они могут быть найдены расчетным путем или выбраны из таблиц [5].
Параметр m имеет свойство аддитивности, т.е.:

,

где m – общий параметр вероятности отказов изделия; n_i – относительное количество отказов данного вида, %; m_i – параметр, соответствующий виду отказов.
Интенсивность отказов маложестких валов определяется:

_.

Вероятность отказов:

.

Cреднее время безотказной работы (средний срок службы) вычисляется по формуле:

Среднее квадратическое отклонение:

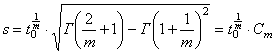
Рассмотрим закономерность рассеивания сроков службы ВМЖ.
Для оценки параметров (среднего срока службы  и стандартной ошибки s), используем метод наименьших квадратов, который здесь выбран как наиболее универсальный способ оценки названных параметров; он позволяет аппроксимировать статистические данные. Аппроксимация статистических данных производится путем линейной интерполяции и решения систем вспомогательных линейных функций при 
;  ; методом наименьших квадратов . Значения функции (квантили) U_p табулированы [5]: 
▪ для нормального закона ;
▪ для логарифмически нормального ; 
▪ для закона Вейбулла ;
▪ для метода испытаний на усталость использован закон Одинга-Вейбулла

По данным [6] механические характеристики металлов хорошо аппроксимируются нормальным законом.
Число циклов до разрушения N при длительных испытаниях хорошо согласуется с логарифмически нормальным распределением, т.е. в этом случае нормально распределена случайная величина  и законом Вейбулла – нормально распределена величина .
При эксплуатации 90 кольцепрядильных хлопковых машин на ниточном комбинате им.С.М.Кирова (г.Санкт-Петербург) в течение 46 месяцев произошел полный отказ ряда рифленых цилиндров. Экспериментальные данные приведены в таблице 1.
Для оценки параметров  и s используем метод наименьших квадратов, который, являясь наиболее универсальным способом оценки названных параметров, позволяет аппроксимировать статистические данные. Аппроксимация статистических данных проводится путем линейных интерполяций и решения систем вспомогательных линейных уравнений: 
- для закона Вейбулла .
Далее определим значения , а также квантиль закона Вейбулла по формуле. Результаты приведены в таблице 1.

Номер опыта	Срок  эксплуатации ti, мес.	Вероятность отказов	Вероятность  безотказной  работы		Квантиль закона Вейбулла
1	6	0,0004	0,9996	0,00040008	–7,824046	1,7917594
2	12	0,0006	0,9994	0,00060018	–7,4184142	2,4849066
3	15	0,0015	0,9985	0,0015011	–6,5022235	2,7080502
4	18	0,0022	0,9978	0,0022024	–6,1182076	2,8903717
5	21	0,0037	0,9963	0,0037068	–5,5975863	3,0445224
6	24	0,0039	0,9961	0,0039076	–5,5448319	3,1780538
7	30	0,0070	0,9930	0,0070246	–4,958337	3,4011973
8	41	0,0096	0,9904	0,0096463	–4,6411808	3,7135720
9	44	0,0278	0,9722	0,0281933	–3,5686709	3,7841896
10	46	0,0280	0,9720	0,028394	–3,5615774	3,8286414

Уравнение  можно записать для всех опытных значений t₁, t₂…t₁₀. Полученные десять уравнений решим аналитически, методом наименьших квадратов. Исходные уравнения 
1) 

2) 
……………………………………………
……………………………………………
9) 

10) 
Cложив почленно 10 исходных уравнений, получим:
, откуда .

Умножив исходные уравнения на коэффициент при m, получим

1)
2)
………………………………………………………
………………………………………………………..
9) 

10) 
Сложив эти уравнения получим:

Далее, подставив в это уравнение, ранее найденное значение , получим .
Подставив найденное значение m в уравнение , получим: ; .
Коэффициенты  и  находим по таблицам приложений математической статистики [3]: ; .
В качестве примера приведен расчет для вытяжного цилиндра:
- средний срок службы или 21 год, что соответствует фактическому сроку эксплуатации и моральной долговечности машин (11 лет 21 года);
- среднее квадратическое отклонение ;
- коэффициент вариации  или .
Гипотезу об усталостном характере разрушения ВМЖ проверим по критерию Колмогорова. Рассчитываем накопленную теоретическую вероятность безотказной работы и по критерию Колмогорова сравниваем ее с действительной. Умножив эти вероятности на общее число наблюдений, получим N_i (теоретическое значение) и  (опытное значение), являющиеся значениями теоретической и опытной функциями распределения. Находим максимум модуля разности значений N_i и . Обозначим эту величину D; . Расчет величины D_max приведен в таблице 2

Срок эксплуатацииti, мес.	Теоретическая вероятность безотказной работы	Действит. вероятн. безотказн. работы	Накопл. теоретич. вероятн.	Накопл. действит. вероятн.
6	0,9997691	0,9996000	0,9997691	0,9996	0,00016
12	0,998962	0,9994000	1,9987311	1,9990	0,00026
15	0,0083162	0,9985000	2,9970473	2,9975	0,00045
18	0,0075003	0,9978000	3,9945476	3,99530	0,00075
21	0,9965095	0,9963000	4,9910571	4,9916	0,00054
24	0,9953395	0,9961000	5,9863966	5,9877	0,00130
30	0,9924486	0,9930000	6,9788452	6,9807	0,00185
41	0,9851844	0,9904000	7,9640296	7,9711	0,00707
44	0,9827530	0,9722000	8,9467826	8,9433	0,00348
46	0,9810238	0,9720000	9,9278064	9,9153	0,01250

Затем получим аргумент критерия Колмогорова
.
По значению при помощи таблиц [5] находится величина Р(), равной вероятности того, что разность D_max превысит полученное значение, т.е. если  гипотеза о согласии теоретического и эмпирического распределения подтверждается.
=0,0125; Р() = 0,99 0,05.
Получен высокий уровень согласия. 
Нами трансформирована стандартная таблица 5 для нахождения для определения  (таблица 3). Таблица позволяет сразу оценить качественную и количественную степень согласия теоретического распределения с опытным.

Таблица 3. Значения и для критерия Колмогорова

	0,3	0,4	0,5	0,6	0,7	0,8	0,9	1	1,1	1,2	1,3	1,4
	1,000	0,997	0,964	0,864	0,711	0,544	0,393	0,270	0,177	0,112	0,068	0,039
Качественная оценка согласия	Высокая			Хорошая			Удовлетво-рительная		Допустимая			Плохо

По таблице 3 при = 0,44 качественная оценка согласия теоретического распределения с полученным опытным – высокая, т.е. гипотеза об усталостном характере разрушения ВМЖ подтверждена качественно и количественно (статистическим анализом).
Графическая интерполяция сроков службы звеньев вытяжного цилиндра приведена на рисунке 1 (на вероятностной бумаге).

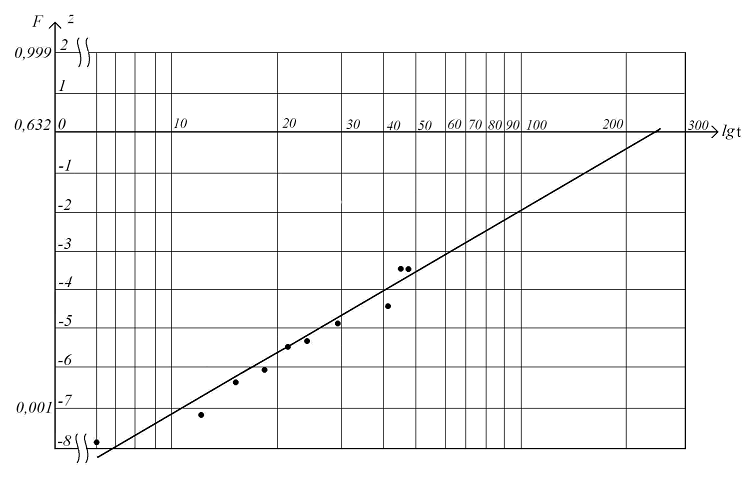
Рисунок 1. Линейная интерполяция распределения сроков службы вытяжных цилиндров кольцепрядильных машин П-76-5М

Выводы: 1) Установлено, что фактические сроки службы ВМЖ распределены по закону Вейбулла, что согласуется с усталостным характером их разрушения; 2) Вероятностно-статистический расчет среднего срока службы вала  мес. или 21 год, что соответствует фактическому сроку эксплуатации и моральной долговечности машин (11 лет 21 года); 3) Результаты исследования учтены при расчете сроков службы изнашиваемых деталей для каталогов запасных частей текстильных машин [7].

1. ГОСТ 27.002-2009. Надежность в технике. Термины и определения.канд.
2. Шорин В.А. Комплексное обеспечение точности и работоспособности валов малой жесткости: автореф. дисс. … канд. техн. наук.- Пенза, 2000. – 21 с.
3. Шор Я.Б. Статистические методы анализа и контроля качества и надежности. – М., «Сов.радио», 1962. – 552 с.
4. Денисова Н.Е. Исследование и разработка метода оценки надежности хлопкопрядильных машин: : автореф. дисс. … канд. техн. наук.- Кострома, 1973. – 20 с.
5. Митропольский А.К. Техника статистических вычислений.- М.: Наука, 1971. – 576 с.
6. Триботехническое материаловедение и триботехнология: учебн. пособие / Н.Е. Денисова, В.А. Шорин, И.Н. Гонтарь [и др.] / под ред. Н.Е. Денисовой.- Пенза: Изд-во Пенз. гос. ун-та. – 2006. – 204 с.
7. Шорин В.А., Гонтарь И.Н. Каталог изнашиваемых деталей ленточных машин Л2-50-1М., Пенза. – Полиграфист, 2000. – 200 с.

Все статьи автора «Шорин Владимир Алексеевич»