Код Хаффмана является одним из самых распространенных методов сжатия данных. Разработан в 1952 г. [1] и до сих пор используется архиваторами либо полностью, либо как один из этапов многоуровневого сжатия. Для профессий, связанных с информационными технологиями, понимание основных идей кода Хаффмана и методов его реализации, будет актуально и полезно.
Код Хаффмана часто описывается в книгах по информационной безопасности [2, 3, 4] Теоретические основы алгоритма, так же описаны во многих источниках [5, 6]. Алгоритм построение бинарного дерева на Java Script описан в работе А.Б. Веретенникова [7]. С.И. Горяинов рассмотрел перестройку бинарных деревьев в алгоритме Хаффмана [8]. Реализацию алгоритма Хаффмана с заданной длиной разбиений входного потока на машинах Тьюринга с почти линейным временем показал М.А.Герасимов [9]. Зарубежные ученые так же применяют рассматриваемый алгоритм в своих исследованиях [10, 11].
Рассмотрим алгоритм на примере кодировки текста. Существует некий алфавит и каждому символу отводится фиксированное количество бит. Алгоритм Хаффмана кодирует каждый символ в зависимости от частоты использования символа. Символ, который чаще других используется, присваивается короткий двоичный код, следовательно, тот символ, который используется реже всего, имеет самый длинный код. После кодировки, сообщение будет весить меньше, чем изначально.
Представим алгоритм на конкретном примере. Закодируем сообщение: «теория_информации». Частоты каждого символа представлены в табл.1.
Таблица 1 – Сообщение «теория_информации»
|
т |
е |
о |
р |
и |
я |
_ |
н |
ф |
м |
а |
ц |
|
1 |
1 |
2 |
2 |
4 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
Теперь будем складывать две самые маленькие частоты. В данном случае сложим частоты символов «т» и «е», а в новом таблице сумму их частот подпишем как «те» (табл.2).
Таблица 2 – Первый этап кодирования сообщения
| те | о | р | и | я | _ | н | ф | м | а | ц |
| 2 | 2 | 2 | 4 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
Теперь снова ищем два символа с наименьшими частотами. Это символы «я» и «_» (табл.3).
Таблица 3 – Второй этап кодирования сообщения
| те | о | р | и | я_ | н | ф | м | а | ц |
| 2 | 2 | 2 | 4 | 2 | 1 | 1 | 1 | 1 | 1 |
Продолжим эти действия до тех пор, пока не останется два столбца. Столбцы, которые будем складывать, выделим полужирным шрифтом (табл.4-11).
Таблица 4 – Третий этап кодирования сообщения
| те | о | Р | и | я_ | нф | м | а | Ц |
| 2 | 2 | 2 | 4 | 2 | 2 | 1 | 1 | 1 |
Таблица 5 – Четвертый этап кодирования сообщения
| те | о | Р | и | я_ | нф | ма | ц |
| 2 | 2 | 2 | 4 | 2 | 2 | 2 | 1 |
Таблица 6 – Пятый этап кодирования сообщения
| те | о | Р | и | я_ | нф | мац |
| 2 | 2 | 2 | 4 | 2 | 2 | 3 |
Таблица 7 – Шестой этап кодирования сообщения
| тео | р | И | я_ | нф | мац |
| 4 | 2 | 4 | 2 | 2 | 3 |
Таблица 8 – Седьмой этап кодирования сообщения
| тео | ря_ | И | нф | мац |
| 4 | 4 | 4 | 2 | 3 |
Таблица 9 – Восьмой этап кодирования сообщения
| тео | ря_ | И | нфмац |
| 4 | 4 | 4 | 5 |
Таблица 10 – Девятый этап кодирования сообщения
| теоря_ | и | нфмац |
| 8 | 4 | 5 |
Таблица 11 – Десятый этап кодирования сообщения
| теоря_ | инфмац |
| 8 | 9 |
Построим бинарное дерево по таблицам. Левым ветвям будем приписывать в коде 0, а правым ветвям 1. Через дефис будем указывать кодировку символа.
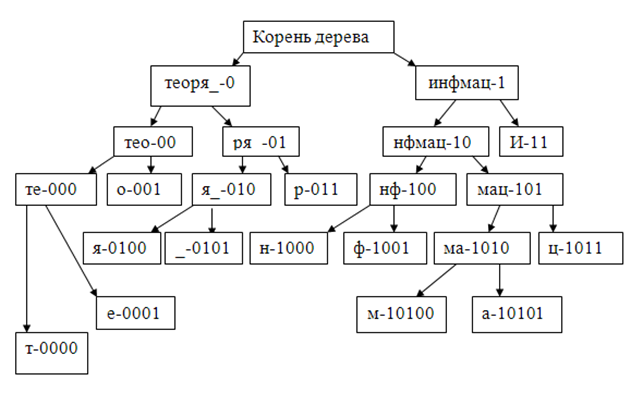
Рисунок 1 – Бинарное дерево
В итоге получилась следующая кодовая таблица (табл.12).
Таблица 12 – Кодовая таблица
| Символ |
Двоичный код |
Частота |
Вес закодированного символа |
| т |
0000 |
1 |
4 бита |
| е |
0001 |
1 |
4 бита |
| о |
001 |
2 |
3 бита |
| р |
011 |
2 |
3 бита |
| и |
11 |
4 |
2 бита |
| я |
0100 |
1 |
4 бита |
| _ |
0101 |
1 |
4 бита |
| н |
1000 |
1 |
4 бита |
| ф |
1001 |
1 |
4 бита |
| м |
10100 |
1 |
5 бит |
| а |
10101 |
1 |
5 бит |
| ц |
1011 |
1 |
4 бита |
Закодированное сообщение будет выглядеть так:
0000000100101111010001011110001001001011101001010110111111
Код Хаффмана является префиксным кодом, т.е. код символа не является частью кода другого символа, следовательно, интерпретируется однозначно. Сравним вес сообщения закодированного с помощью ASCII и сообщение, закодированное по алгоритму Хаффмана.
ASCII:
17 * 8 бит = 122 бита
Код Хаффмана:
4 бита + 4 бита + 2 * 3 бита + 2 * 3 бита + 4 * 2 бита + 4 бита + 4 бита + 4 бита + 4 бита + 5 бит + 5 бит + 4 бита = 58 бит
Сообщение, закодированное с помощью алгоритма Хаффмана, весит примерно в два раза меньше.
Реализация приложения на PHP.
Приложение должно выполнять следующие действия:
- Составить таблицу частот (вероятностей появления символов)
- Построить бинарное дерево
- Сгенерировать код для каждого символа
- Вывести закодированный результат
Приводим образец кода, в данном случае, функцию составления таблиц частот (рис.2).

Рисунок 2 – Образец кода
Для ввода сообщения приложение выглядит на рис.3.
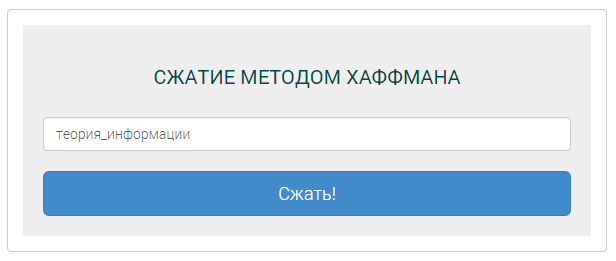
Рисунок 3 – Ввод сообщения
После ввода сообщения и нажатия кнопки «Сжать», приложение выдает результат (рис.4).
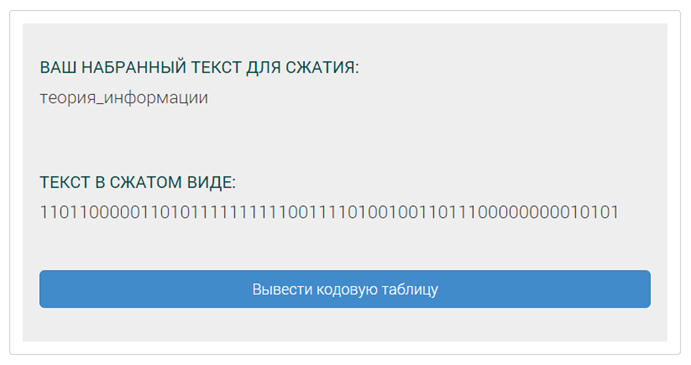
Рисунок 4 – Сгенерированное сообщение
Отметим при этом, что закодированное сообщение в приложении отличается от варианта выше. Выведем кодовую таблицу для сравнения с таблицей в разделе теория (рис.5).
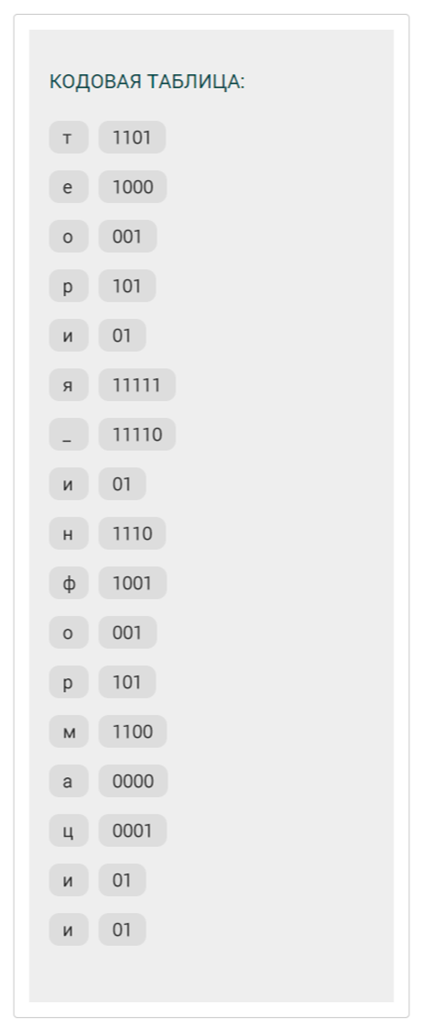
Рисунок 5 – Кодовая таблица
Заметим, что код каждому символу присвоен другой. Вызвано это тем, что изначально много символов, с одинаковой частотой и в процессе построение дерева, часто был выбор в сложении частот, который при этом не влиял на эффективность алгоритма, или распределение символа в другую ветвь, что также влияло на итоговый код символа. Однако по-прежнему самый частый символ «и» закодирован в 2 бита, символы «р» и «о» 3 битами, что в итоге говорит о том, что вес закодированного сообщения по-прежнему равен 58 бит.
Проведенное исследование может быть использовано в преподавании различных дисциплин, связанных с передачей информации.
Библиографический список
-
Huffman D. A. et al. A method for the construction of minimum redundancy codes // Proceedings of the IRE. 1952. Т. 40. №. 9. С. 1098-1101.
-
Партыка Т.Л., Попов И.И. Информационная безопасность: учебное пособие. М.: Форум, 2012.
-
Петров С.В., Слинькова И.П., Гафнер В.В. Информационная безопасность: учебное пособие. М.: АРТА, 2012.
-
Баженов Р.И. Информационная безопасность и защита информации: практикум. Биробиджан: Изд-во ГОУВПО «ДВГСГА», 2011. 140 с.
-
Кормен Т. Х., Лейзерсон Ч. И., Ривест Р. Л., Штайн К. Алгоритмы: построение и анализ. М.:Вильямс, 2006.
-
Семенов Ю.А. Алгоритмы и протоколы каналов и сетей передачи данных. М.: Интернет-Университет Информационных Технологий, 2007. 638 с.
-
Веретенников А.Б. Алгоритм Хаффмана [электронный ресурс]. URL: http://www.veretennikov.org/Default.aspx?f=USU%2fDefault.aspx
-
Горяинов С.И. Перестройка бинарных деревьев в алгоритме Хаффмана // Программные системы и вычислительные методы. 2014. № 4. С. 464-471.
-
Герасимов М.А. Реализация алгоритма Хаффмана с заданной длиной разбиений входного потока на машинах Тьюринга с почти линейным временем // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. 2010. № 3. С. 100-105.
-
Liu Y. K., Žalik B. An efficient chain code with Huffman coding // Pattern Recognition. 2005. Т. 38. №. 4. С. 553-557.
-
Lin Y. K., Huang S. C., Yang C. H. A fast algorithm for Huffman decoding based on a recursion Huffman tree // Journal of Systems and Software. 2012. Т. 85. №. 4. С. 974-980.
Количество просмотров публикации: Please wait


