Во второй части работы приведены стационарные результаты расчетов полей температуры, функции тока, напряженности вихря, радиальной и меридиональной составляющих магнитной индукции, а также распределение чисел Нуссельта на внутренней и внешней границе сферического слоя для различных значений числа Грасгофа, параметра магнитного взаимодействия и граничных условий для температуры. Толщина сферического слоя ![]() =2,5.
=2,5.
Для температуры задавались два типа граничных условий:
1. На внутренней и внешней поверхности слоя граничные условия первого рода (постоянные значения температуры): ![]()
![]() . Для заданных граничных условий постоянная величина
. Для заданных граничных условий постоянная величина ![]() и число Грасгофа вычислялась по формулам:
и число Грасгофа вычислялась по формулам: 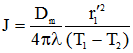 ;
; ![]() . Обозначим эти граничные условия как ГУ-1.
. Обозначим эти граничные условия как ГУ-1.
2. На внутренней поверхности слоя граничное условие первого рода (постоянное значение температуры), а на внешней поверхности граничное условие второго рода (отвод тепла) [2]: ![]()
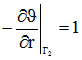 . Для заданных граничных условий постоянная величина
. Для заданных граничных условий постоянная величина ![]() вычислялась по формуле:
вычислялась по формуле: 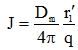 . Обозначим эти граничные условия как ГУ-2.
. Обозначим эти граничные условия как ГУ-2.
На рисунках 16 приведены поля температуры, функции тока, напряженности вихря, радиальной и меридиональной составляющей магнитной индукции и распределения чисел Нуссельта.
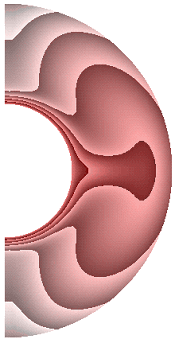
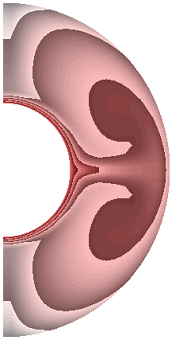
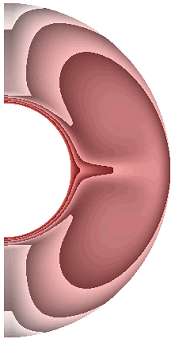
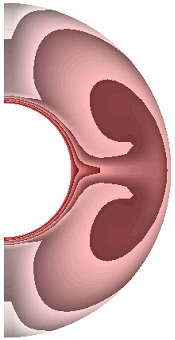
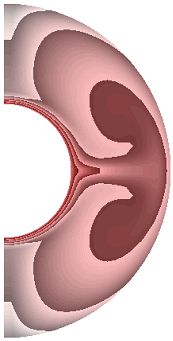
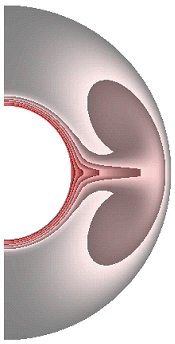
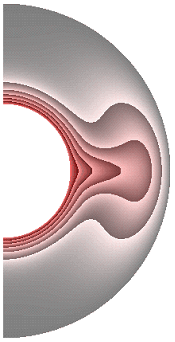
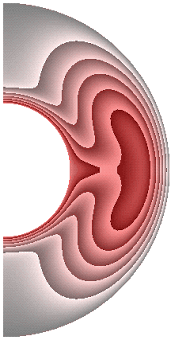
На рисунке 1 приведены результаты расчетов поля температуры.
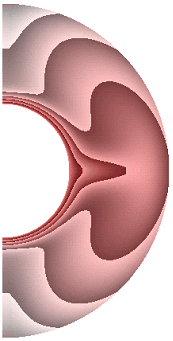
а б в г д

е ж з и к
Для всех полученных результатов, где каждый рисунок представлен десятью фрагментами, соответствующими режимам их расчета, приняты следующие обозначения:
а(![]()
![]()
![]()
![]() , ГУ-2),
, ГУ-2),
б(![]()
![]()
![]()
![]() , ГУ-2),
, ГУ-2),
в (![]()
![]() , ГУ-2),
, ГУ-2),
г (![]()
![]() , ГУ-2),
, ГУ-2),
д (![]()
![]() , ГУ-2),
, ГУ-2),
е (![]()
![]() , ГУ-2),
, ГУ-2),
ж (![]()
![]() , ГУ-1),
, ГУ-1),
з (![]()
![]() , ГУ-1),
, ГУ-1),
и (![]()
![]() , ГУ-1),
, ГУ-1),
к (![]()
![]() , ГУ-1).
, ГУ-1).
Для всех случаев, за исключением результата рис.1, ж, теплообмен в слое осуществляется конвекцией. Диапазоны изменения температуры для результатов рис. 1, а-к составляют соответственно [19,413; 1], [17,316; 1], [12,500; 1], [10,904; 1], [12,505; 1], [12,500; 1], [0; 1], [0; 1], [0; 1], [0; 1]. Для температурных граничных условий типа ГУ-2 учет джоулевой диссипации и уменьшение параметра магнитного взаимодействия ![]() ведет к уменьшению диапазона изменения температуры,
ведет к уменьшению диапазона изменения температуры,
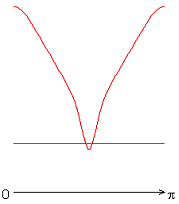
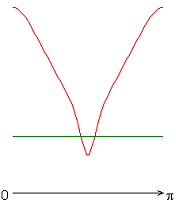
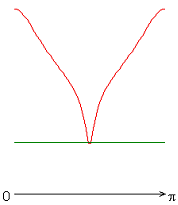
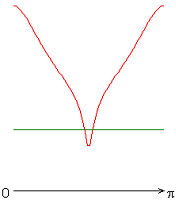
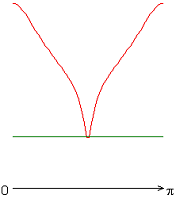
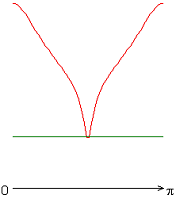
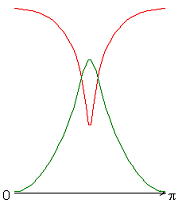
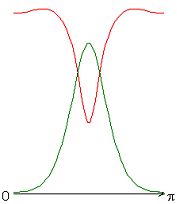
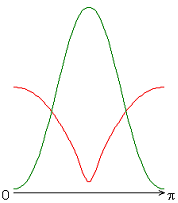
На рисунке 2 приведены результаты расчетов локальных чисел Нуссельта на внутренней (красная линия) и внешней (зеленая линия) поверхности сферического слоя.
а б в г д

е ж з и к
Следует отметить, что согласно заданному граничному условию для температуры на внешней границе слоя (ГУ-2, рис. 2, а-е), распределение локальных чисел Нуссельта совпадает с осредненным и принимает постоянное значение ![]() 25 (здесь и далее). Распределения локальных чисел Нуссельта на внутренней границе слоя имеют минимум в случае граничных условий типа ГУ-2 (рис. 2, а-е), а в случае граничных условий типа ГУ-1 (за исключением результата рис. 2, ж) максимум (на внешней границе слоя) и минимум (на внутренней границе слоя) (рис. 2, з-к) при значении полярного угла
25 (здесь и далее). Распределения локальных чисел Нуссельта на внутренней границе слоя имеют минимум в случае граничных условий типа ГУ-2 (рис. 2, а-е), а в случае граничных условий типа ГУ-1 (за исключением результата рис. 2, ж) максимум (на внешней границе слоя) и минимум (на внутренней границе слоя) (рис. 2, з-к) при значении полярного угла ![]() (экваториальная плоскость). Значение осредненного и диапазон изменения локальных чисел Нуссельта:
(экваториальная плоскость). Значение осредненного и диапазон изменения локальных чисел Нуссельта:
![]() 57,355; 22,068
57,355; 22,068![]() 95,105;
95,105; ![]() 47,389; 17,068
47,389; 17,068![]() 82,235;
82,235;
![]() 57,353; 24,654
57,353; 24,654![]() 90,148;
90,148; ![]() 46,124; 18,710
46,124; 18,710![]() 76,088;
76,088;
![]() 57,354; 24,655
57,354; 24,655![]() 90,150;
90,150; ![]() 57,354; 24,655
57,354; 24,655![]() 90,150;
90,150;
соответственно для результатов рис. 2, а-е. И для результатов рис. 2, ж-к:
![]() 1,569;
1,569; ![]() 0,684;
0,684;
![]() 5,689; 2,613
5,689; 2,613![]() 7,054;
7,054; ![]() 2,480; 0,052
2,480; 0,052![]() 5,074;
5,074;
![]() 3,213; 1,504
3,213; 1,504![]() 3,900;
3,900; ![]() 1,401; 0,038
1,401; 0,038![]() 3,182;
3,182;
![]() 2,884; 0,510
2,884; 0,510![]() 5,017;
5,017; ![]() 5,581; 0,196
5,581; 0,196![]() 8,790.
8,790.
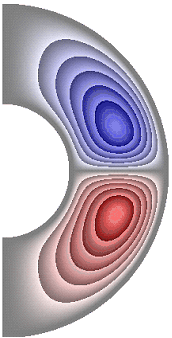
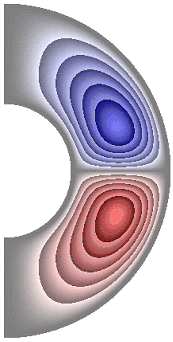
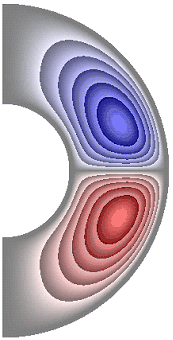
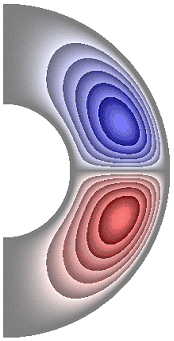
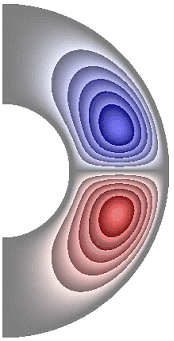
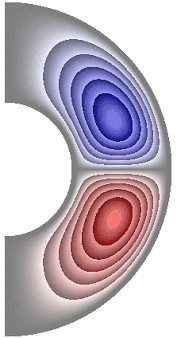
На рисунке 3 приведены результаты расчетов поля функции тока. Для всех случаев в слое образуются две конвективные ячейки. Для температурных граничных условий ГУ-2 и ГУ-1 жидкость в северном полушарии слоя движется по часовой стрелке (синий цвет значения функции тока отрицательные), а в южном против часовой стрелки (красный цвет значения положительные) (рис. 3, а-е, з-к). Исключение составляет результат, полученный в режиме теплопроводности при значении числа Грасгофа ![]() (рис. 3, ж). Максимальное значение функции тока соответственно
(рис. 3, ж). Максимальное значение функции тока соответственно ![]() 1,51·10; 1,42·10; 4,91·10; 4,57·10; 4,91·10; 4,91·10; 8,32·10-6; 4,75·10; 1,04·10; 1,53·10.
1,51·10; 1,42·10; 4,91·10; 4,57·10; 4,91·10; 4,91·10; 8,32·10-6; 4,75·10; 1,04·10; 1,53·10.
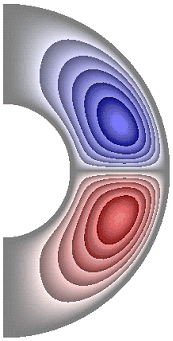
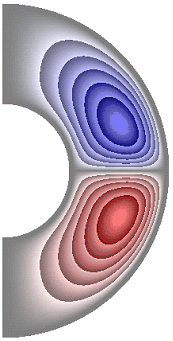
а б в г д
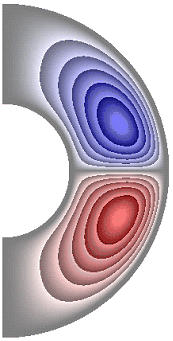
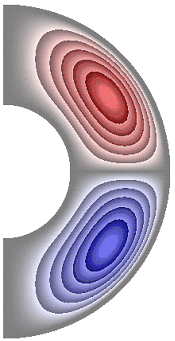
е ж з и к
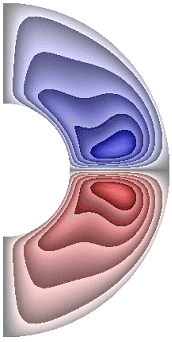
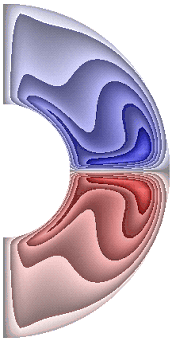
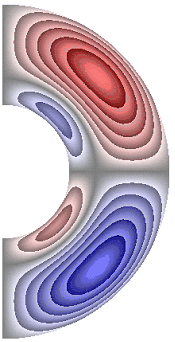
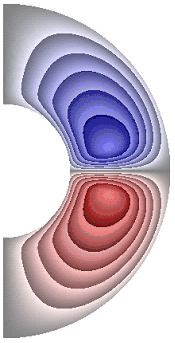
На рисунке 4 приведены результаты расчетов поля напряженности вихря. Для всех режимов в слое, за исключением случая, представленного на рис. 4, ж, образуются два крупномасштабных вихря. В зависимости от режима структура вихрей, хотя и незначительно, но изменяется. Для результатов рис. 4, а-е, з-к в северном полушарии жидкость движется по часовой стрелке (синий цвет значения отрицательные), а в южном против часовой стрелки (красный цвет значения положительные). Для температурных граничных условий ГУ-1 форма вихрей отлична от формы вихрей при температурных граничных условий ГУ-2 (рис. 4, ж, и, к).
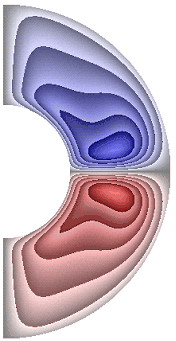
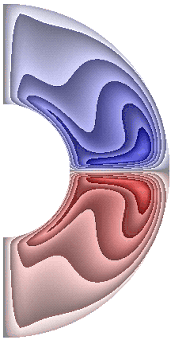
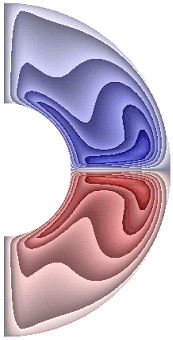
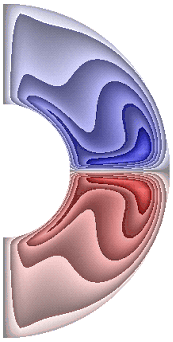
а б в г д


е ж з и к
Для результата, представленного на рис. 4, ж, вблизи внутренней границы слоя образуются еще два мелкомасштабных вихря, в которых направление движения жидкости изменяется на противоположное по сравнению с направлением движения жидкости в крупномасштабных вихрях. Максимальная интенсивность вихрей ![]() 8,55·10; 7,91·10; 2,96·102; 2,71·102; 2,96·102; 2,96·102; 4,89·10-5; 2,88·102; 6,02·10; 7,62·10 соответственно для результатов рис. 4, а-к.
8,55·10; 7,91·10; 2,96·102; 2,71·102; 2,96·102; 2,96·102; 4,89·10-5; 2,88·102; 6,02·10; 7,62·10 соответственно для результатов рис. 4, а-к.
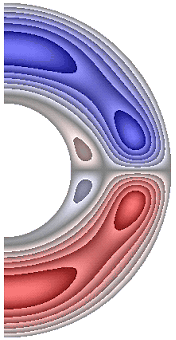
На рисунке 5 приведены результаты расчетов поля радиальной составляющей магнитной индукции.
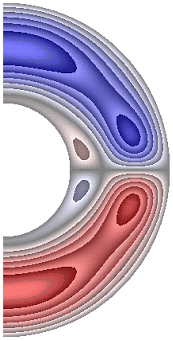
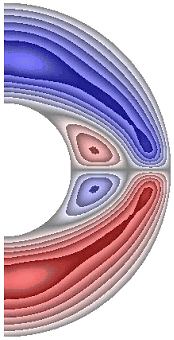
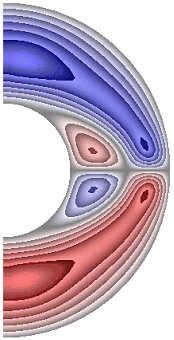

а б в г д



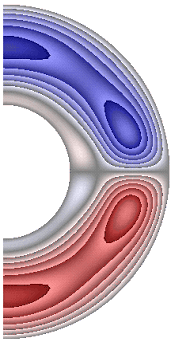
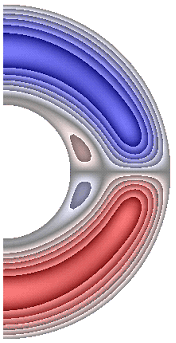
е ж з и к
Радиальная составляющая магнитной индукции для всех случаев в северном полушарии принимает отрицательные значения, за исключением небольшой области вблизи внутренней границы слоя, а в южном – положительные, за исключением небольшой области вблизи внутренней поверхности слоя. В экваториальной части слоя у внутренней границы слоя образуются две небольшие области, в которых значения радиальной составляющей магнитной индукции изменяют знак (с плюса на минус). В зависимости от режима структура вихрей претерпевает, хотя и небольшие, изменения. Максимальное значение радиальной составляющей магнитной индукции в слое ![]() 1,23·10-3; 1,24·10-3; 2,58·10-3; 2,52·10-3; 2,58·10-3; 2,58·10-3; 8,55·10-4; 2,55·10-3; 1,03·10-3; 1,13·10-3соответственно для результатов рис. 5, а-к.
1,23·10-3; 1,24·10-3; 2,58·10-3; 2,52·10-3; 2,58·10-3; 2,58·10-3; 8,55·10-4; 2,55·10-3; 1,03·10-3; 1,13·10-3соответственно для результатов рис. 5, а-к.
На рисунке 6 приведены результаты расчетов поля меридиональной составляющей магнитной индукции. Меридиональная составляющая магнитной индукции для всех случаев принимает положительные значения практически во всем слое, за исключением области у внутренней границы слоя, в которой значения меридиональной составляющей магнитной индукции отрицательные. В зависимости от режима структура поля меридиональной составляющей магнитной индукции в слое изменяется. Максимальное значение меридиональной составляющей магнитной индукции в слое ![]() 1,00·10-2; 1,00·10-2; 1,05·10-2; 1,04·10-2; 1,05·10-2; 1,05·10-2; 1,00·10-2; 1,07·10-2; 1,00·10-2; 1,00·10-2; соответственно для результатов рис. 5, а-к.
1,00·10-2; 1,00·10-2; 1,05·10-2; 1,04·10-2; 1,05·10-2; 1,05·10-2; 1,00·10-2; 1,07·10-2; 1,00·10-2; 1,00·10-2; соответственно для результатов рис. 5, а-к.





а б в г д





е ж з и к
Анализ полученных результатов позволяет сделать следующие выводы:
для всех режимов и температурных граничных условий (за исключением случая при ![]() ) теплообмен в слое осуществляется конвекцией;
) теплообмен в слое осуществляется конвекцией;
характер изменения распределений чисел Нуссельта при ГУ-1 и Гу-2 имеет значительные отличия;
при ГУ-2 учет джоулевой диссипации приводит к уменьшению диапазона изменения температуры, значений функции тока и вихря в слое при тех же самых критериях подобия;
для всех режимов и температурных граничных условий в расчетной области образуются две конвективные ячейки и два вихря с одинаковой структурой течения, за исключением случая при ![]() . Форма вихрей при ГУ-1 и Гу-2 различна;
. Форма вихрей при ГУ-1 и Гу-2 различна;
структура радиальной и меридиональной составляющих магнитной индукции зависит от безразмерных критериев подобия и типа граничного условия для температуры;
полученные результаты могут быть применены для моделирования различных условий при изучении тепловых и гидродинамических процессов в сферических слоях, например в жидком ядре Земли.
Количество просмотров публикации: Please wait


