Введение
Твердофазные цепные реакции являются относительно новым классом химических процессов [1, с. 152, 2, с. 95, 3, с. 107], экспериментально и теоретически обнаруженным в лабораториях Кемеровского государственного и Томского Политехнического университетов [4, с. 15, 5, с. 77, 6, с. 19]. Показано, что в рамках бимолекулярной модели твердофазной цепной реакции может быть описан целый комплекс экспериментальных данных по лазерному инициированию азида серебра, в том числе: вероятностный характер взрыва [1, с. 152, 7, с. 44, 8, с. 14], зависимость критической плотности энергии от длительности импульса и длины волны лазерного излучения [9, с. 5, 10, с. 99], влияние размера монокристалла [5, с. 77, 11, с. 37, 12, с. 53] и диаметра зоны облучения [13, с. 106, 14, с. 69] на порог лазерного инициирования, зависимость индукционного периода от плотности энергии импульса. Показано, что распространение взрывной реакции в азиде серебра связано с движением волны твердофазной цепной реакции [15, с. 29, 16, с. 97]. В то же время кинетика взрывного свечения азида серебра, полученная в работе [14, с. 70] пока не нашла удовлетворительного описания в рамках цепной концепции. Актуальность исследования определяется необходимостью разработки оптических детонаторов на основе инициирующих и вторичных взрывчатых веществ [17, с. 55, 18, с. 40, 19, с. 686]. Цель работы: разработка модели энергетической твердофазной цепной реакции, позволяющей описать кинетические зависимости взрывного свечения азида серебра. 
Модель твердофазной цепной реакции
В [1, с. 152] сформулирован ряд основных свойств энергетической твердофазной цепной реакции:
1. Носителями цепи являются электронные возбуждения кристалла: электроны, дырки, экситоны. 
2. Порядок стадии рекомбинации носителей цепи должен быть меньше порядка стадии разветвления. В противном случае порог инициирования не существует, и кристалл взрывается от единичного затравочного носителя цепи.
3. Должен существовать эффективный механизм передачи энергии, выделяющейся в акте разветвления цепи, электронной подсистеме вещества с генерацией новых электронных возбуждений.
В работе [6, с. 19] рассмотрены механизмы дезактивации возбужденных молекул в матрице азида серебра, образовавшихся при взаимодействии двух азид-радикалов в кристаллической решетке. Показано, что при дезактивации электронно-возбужденной молекулы азота, возможна генерация электронно-дырочной пары, пары дефектов по Френкелю, или передача энергии зонной дырки с образованием горячего носителя заряда и переходом энергии в тепло [20, с. 45]. Причем первый процесс более эффективен, чем остальные [6, с. 19]. При дезактивации колебательно-возбужденной молекулы азота возможен выброс дырки с энергетического уровня продукта, либо передача энергии зонному носителя заряда. Согласно оценкам, безразмерный коэффициент, показывающий эффективность второго процесса относительно первого составляет порядка 100 [6, с. 19].
С учетом представлений о дезактивации возбужденных продуктов кинетика твердофазной цепной реакции будет описываться системой уравнений:
 (1)
где p – концентрация носителей цепи, А – концентрация невозбужденных узлов анионной подрешетки образца, G – скорость генерации носителей цепи, k_r – константа скорости рекомбинации носителей цепи, k₂ – константа скорости бимолекулярной реакции разветвления цепи, г₁, г₂ - безразмерные параметры, характеризующие вероятность генерации электронных возбуждений (разветвления) при дезактивации электронно- и колебательно- возбужденных молекул азота соответственно. Согласно сделанным в работах [6, с. 19, 20, 45] оценкам, г₁, < 1, г₂ ~ 100. Темп генерации задавался в виде , где эффективная константа скорости импульса связана с его длительностью на полувысоте ф выражением 
Анализ модели
Рассмотрим процесс развития реакции при произвольной степени разложения. Нас будет интересовать вид кинетических зависимостей концентрации носителей цепи и исходного вещества, а также соотношение между их концентрациями. Теоретическое исследование кинетических закономерностей разветвленных цепных реакций в газовой фазе было проведено Семеновым Н.Н. [21, с. 95]. Показано, что существует соотношение между концентрацией исходного вещества и концентрацией носителей цепи, которое было подтверждено экспериментально:
, (2)
где о – концентрация носителей цепи, нормированная на исходную концентрацию горючей смеси, з – степень выгорания, p₁, p₀ – критическое и начальное давление. В случае цепной реакции с коэффициентом размножения 3/2 и суммарной концентрацией носителей цепи, исходного вещества и продуктов реакции равной числу Лошмидта L, формулу (2) можно переписать в виде:
 (3)
где p - концентрация носителей цепи, в – доля неразложенного вещества. Такой результат получается при непосредственном перенесении закономерностей разветвленный газофазных цепных реакций в область твердофазных цепных реакций.
Получим соотношение подобное (2) в рамках модели (1). Процесс будем рассматривать в пренебрежении рекомбинацией, так как при больших концентрациях носителей цепи последний член в уравнениях (1) становится основным. Система кинетических уравнений примет вид:
 (4) 
Для получения соотношения между p и А разделим одно из уравнений (4) на другое:
. (5)
Данное дифференциальное уравнение связывает концентрации исходного вещества и носителей цепи. Левая часть этого уравнения является однородной функцией p/A. Интеграл уравнения (5) имеет вид:
, (6)
где для четырех безразмерных коэффициентов, определяемых значениями параметров г₁ и г₂, использованы обозначения:


.
Отметим, что соотношение (6) отличается от формулы (3), связывающей концентрации носителей цепи и исходного вещества в случае разветвленных газофазных цепных реакций. Причина данного различия состоит в различной записи членов отвечающих за разветвление цепи, которое определяется условиями передачи энергии. 
Рассмотрим соотношение (2) для газофазных цепных реакций используя вероятностный подход к кинетике разветвленных цепных реакций. Согласно последнему, носитель цепи может с некоторой вероятностью w участвовать в разветвлении цепи, что приведет к рождению новых носителей, либо с вероятностью 1 - w участвовать в обрыве цепи. Будем полагать, что газофазная разветвленная цепная реакция является энергетической. Носитель цепи может вступить во взаимодействие с молекулой исходного вещества и при передаче ей энергии произойдет разветвление цепи. Также носитель может вступить во взаимодействие с продуктом реакции (или любой инертной частицей) и передать ей энергию. В результате этого сам носитель погибнет, а возбуждение инертной частицы быстро диссипируется в тепло: произойдет обрыв цепи. В газовой фазе первый и второй процессы происходят при столкновениях носителя цепи с соответствующей частицей. В силу того, что носитель цепи уже является возбужденной частицей, энергия активации для обеих реакций будет близка к нулю, и константа скорости будет в основном определяться сечением соударения. Так как сечения соударения слабо различаются для различных малых молекул, константы скорости обрыва и разветвления будут близки, а вероятность разветвления будет приблизительно равна отношению концентрации исходного вещества к общей концентрации газа (мольной доли исходного вещества). Последнее утверждение, фактически является главным предположением, приводящим к формуле (2). 
Проведенное в [6, с. 19, 20, 45] рассмотрение процесса передачи энергии возбужденных молекул азота кристаллической решетке азида серебра позволило сделать вывод: константы скорости дезактивации при взаимодействии возбужденной молекулы азота с носителем цепи значительно отличаются от соответствующего значения при взаимодействии с невозбужденным узлом решетки. Кроме того, константа скорости дезактивации при взаимодействии с продуктом реакции – молекулами азота, находящимися в узлах кристаллической решетки – по-видимому, равна нулю. Действительно, даже если предположить существование эффективного обмена энергией между молекулами азота через кристаллическую решетку азида серебра, передача от возбужденной к невозбужденной молекуле одного колебательного кванта приведет к повышению энергии последней на 0.294 эВ. Но эта величина становится сопоставима с тепловой энергией лишь при температурах близких к адиабатической температуре взрыва. Значит, данный процесс практически не приводит к диссипации энергии. Изложенные соображения позволяют заключить, что в случае твердофазных цепных реакций вероятность разветвления цепи не пропорциональна мольной доли неразложившегося вещества, что и приводит к брутто-зависимости (6). 
Кинетическая зависимость взрывного свечения 
Одним из основных результатов экспериментальных исследований, являются полученные осциллограммы взрывного свечения, фиксируемого при помощи специальной методики наблюдения из зоны воздействия импульса. Данные осциллограммы дают наиболее достоверную информацию о кинетике развития взрывного разложения. Показано [14, с. 70], что при более чем двух кратном превышении порога инициирования зарождение реакции в зоне воздействия лазерного импульса происходит практически гомогенно, а момент изменения фазового состояния вещества близок к максимуму свечения из зоны воздействия. Таким образом, данное свечение является свечением еще твердого образца и отражает кинетику развития реакции. 
В случае внутризонной люминесценции скорость генерации горячих дырок будет пропорциональна скорости разветвления цепи. Поэтому, нормированная на амплитуду интенсивность свечения равна квадрату отношения концентрации дырок к их максимальному значению:
. (7)

Полученное выражение позволяет по известной кинетической зависимости концентрации дырок рассчитать кинетическую зависимость взрывного свечения. 
Обратная кинетическая задача решалась следующим образом. В начале система уравнений (1) решалась численно при заданном превышении порога инициирования с использованием метода Рунге-Кутта 5-го порядка с переменным шагом по времени и относительной погрешностью на шаге интегрирования не более 10^-9. Далее методом линейной интерполяции вычислялись значения нормированной интенсивности свечения в моменты времени, соответствующие имеющемуся цифровому сигналу. После этого на отрезке от момента времени, соответствующему 5% амплитуды сигнала на его переднем фронте, до максимума сигнала (ориентировочный момент разрушения образца), вычислялась сумма квадратов отклонений экспериментальной зависимости от теоретической. Сумма квадратов отклонений минимизировалась методом Нелдера-Мида при варьировании параметров модели, в качестве которых выступали константа рекомбинации и безразмерный коэффициент. 
Константа скорости бимолекулярной реакции не варьировалась, так как было установлено при решении прямой задачи, что ее значение определяет порог инициирования, тогда как вид кинетических зависимостей реагентов при заданном превышении порога инициирования практически не меняется при ее вариации. 
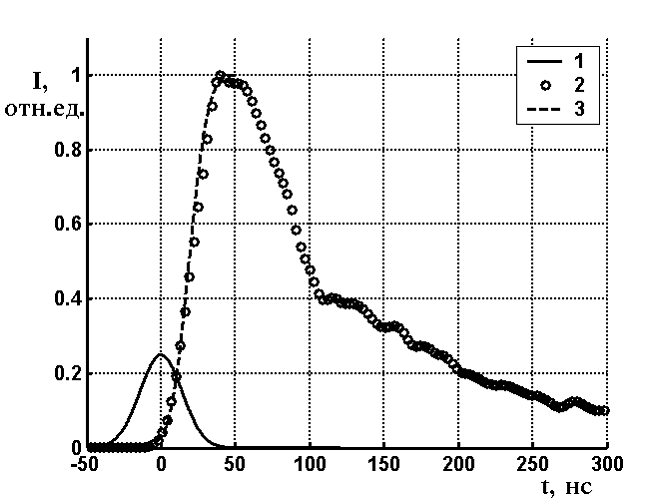
Результат обработки одной из осциллограмм приведен на рис. 1. Значения варьируемых параметров, полученных при обработке 30 осциллограмм взрывного свечения составили:  = (5 ± 1)•10⁷ с^-1,  = 140 ± 20. Полученные параметры согласуются с приведенными ранее априорными оценками и значениями, полученными при обработке других экспериментальных зависимостей [5, с. 77].
Заключение
Сформулирована модель энергетической твердофазной цепной реакции, в которой разветвление цепи протекает при дезактивации возбужденных продуктов в кристаллической решетке с генерацией электронно-дырочных пар. Показано, что в рамках сформулированной модели становится возможным количественное описание кинетической зависимости взрывного свечения азида серебра, причем полученные варьируемые параметры согласуются с оценками констант скоростей дезактивации молекул азота в матрице азида серебра. Работа выполнена при финансовой поддержке Министерства образования и науки РФ госзадание № 2014/64 и Российского Фонда Фундаментальных Исследований (№ 14-03-00534 А).

1. Кригер В.Г., Каленский А.В. Инициирование азидов тяжелых металлов импульсным излучением // Химическая физика. 1995. T. 14. № 4. C. 152 – 160.
2. Адуев Б.П., Алукер Э.Д., Кречетов А.Г. Дивакансионная модель инициирования азидов тяжелых металлов // Физика горения и взрыва. 2004. Т. 40. № 2. С. 94 – 99.
3. Корепанов В.И., Лисицын В.М., Олешко В.И., Ципилев В.П. К вопросу о кинетике и механизме взрывного разложения азидов тяжелых металлов // Физика горения и взрыва. 2006. Т. 42. № 1. С. 106 – 119.
4. Кригер В.Г., Каленский А.В., Захаров Ю.А., Ципилев В.П.. Механизм твердофазной цепной реакции.// Материаловедение. 2006. №9. С. 14 – 21.
5. Кригер В.Г., Каленский А.В., Ананьева М.В., Боровикова А.П.. Зависимость критической плотности энергии инициирования взрывного разложения азида серебра от размеров монокристаллов // Физика горения и взрыва. 2008. Т. 44. № 2. С. 76 – 78.
6. Кригер В.Г., Каленский А.В., Звеков А.А.. Релаксация электронно-возбужденных продуктов твердофазной реакции в кристаллической решетке // Химическая физика. 2012. Т. 31. № 1. С. 18 – 22.
7. Боровикова А.П., Ананьева М.В., Одинцова О.В. Природа стадии обрыва цепи разветвленных твердофазных цепных реакций // Молодой ученый. 2014. № 15 (74). С. 41 – 45.
8. Ananyeva M.V., Kriger V.G., Kalensii A.V. и др. Comparative analysis of energetic materials explosion chain and thermal mechanisms // Известия высших учебных заведений. Физика. 2012. Т. 55. № 11-3. С. 13 – 17.
9. Кригер В.Г., Каленский А.В., Коньков В.В. Пороговая энергия инициирования азида серебра эксимерным лазером // Материаловедение. 2003. № 7. С. 2 – 7.
10. Каленский А.В., Звеков А.А., Ананьева М.В. и др. П. Влияние длины волны лазерного излучения на критическую плотность энергии инициирования энергетических материалов // Физика горения и взрыва. 2014. Т. 50. № 3. С. 98 – 104.
11. Боровикова А.П., Каленский А.В., Зыков И.Ю. Пространственно-временные характеристики волны горения в азиде серебра// Аспирант. 2014. №3. С. 37 – 42.
12. Ананьева М.В., Каленский А.В. Инициирование взрывного разложения микрокристаллов азида серебра // Молодой ученый. 2014. № 19. С. 52 – 55.
13. Кригер В.Г., Ципилев В.П., Каленский А.В., Звеков А.А. Взрывное разложение монокристаллов азида серебра при различных диаметрах зоны облучения // Физика горения и взрыва. 2009. Т. 45. № 6. С. 105 – 107.
14. Кригер В.Г., Каленский А.В., Звеков А.А. Определение начала механического разрушения кристаллов азида серебра, инициированных лазерным импульсом // Физика горения и взрыва. 2010. Т. 46. № 1. С. 69 – 72.
15. Кригер В. Г., Каленский А. В., Звеков А. А. и др. Определение пространственных характеристик волны цепной реакции в азиде серебра // Химическая физика. 2014. Т. 33. № 8. С. 22 – 29.
16. Боровикова А.П., Каленский А.В. Методика моделирования распространения взрывного разложения азида серебра// Аспирант. 2014. №4. С. 96 – 100.
17. Кригер В.Г. , Каленский А.В., Звеков А.А. и др. Влияние эффективности поглощения лазерного излучения на температуру разогрева включения в прозрачных средах // Физика горения и взрыва. 2012. Т. 48. № 6. С. 54 – 58.
18. Адуев Б.П., Нурмухаметов Д.Р., Фурега Р.И. и др. Взрывчатое разложение тэна с нанодобавками алюминия при воздействии импульсного лазерного излучения различной длины волны // Химическая физика. 2013. Т. 32. № 8. С. 39 – 42.
19. Zvekov A.A., Ananyeva M.V., Kalenskii A.V. и др. Regularities of light diffusion in the compo site material pentaery thriol tetranitrate – nickel // Наносистемы: физика, химия, математика. 2014. Т. 5. № 5. С. 685 – 691.
20. Гришаева Е.А., Каленский А.В, Ананьева М.В. и др. Неизотермическая модель разветвленной цепной реакции взрывного разложения // Фундаментальные проблемы современного материаловедения. 2013. Т. 10. № 1. С. 44 – 49.
21. Семенов, Н. Н. Развитие теории цепных реакций и теплового воспламенения // М.: Наука. 1969. 95 с.

Все статьи автора «Каленский Александр Васильевич»