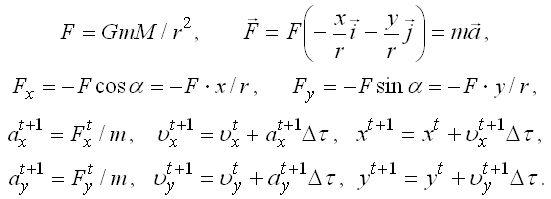1. Введение. Актуальность проблемы
Изучение темы “Движение частицы в центрально–симметричном поле” имеет большое значение для понимания курсов физики и астрономии. К обсуждению проблемы движения точки в поле центральной силы сводится задача двух тел; ее изучение также предполагает рассмотрение законов движения планет, обращения спутников вокруг Земли, движения электронов вокруг ядра (теория Бора), опыта Резерфорда по рассеянию альфа–частиц ядрами атомов золота, движения сферического маятника, шарика в осесимметричной потенциальной яме и т.д.
Один из эффективных способов изучения этого вопроса состоит в применении компьютерных моделей. Используя специальные учебные программы, написанные в Delphi и Visual Basic, можно промоделировать движение частицы в центрально-симметричном поле и установить соответствующие закономерности. Недостаток этой методики состоит в том, что студент не участвует в создании программы и часто работает с ними, не понимая, как вычисляются координаты и скорость частицы. Альтернативный подход заключается в применении небольших учебных программ (10–15 строк), которые студенты способны быстро набрать во время занятия, а затем выполнить серию учебных вычислительных экспериментов. В работах [3, 4] представлены примеры таких программ на языке Pascal.
Настоящая статья посвящена разработке методики проведения лабораторной работы “Изучение движения точки в поле центральной силы” на базе электронных таблиц Excel. Она состоит в теоретическом изучении метода компьютерного моделирования, создании двух или более программ на языке Visual Basic и проведении серии вычислительных экспериментов, подтверждающих законы Кеплера и некоторые другие утверждения. В статье фактически представлена инструкция по выполнению этой работы.
Как известно, школьный и вузовский курсы информатики предполагают освоение табличного процессора MS Excel, который является мощным программным средством, объединяющим в себе электронные таблицы, средства визуального программирования и графический модуль, позволяющий построить различные диаграммы, графики и поверхности. Хотя пакет MS Excel имеет меньше возможностей по сравнению со специализированными пакетами (MathCad, MathLab, Math и т.д.), он позволяет реализовать простейшие алгоритмы численного решения дифференциальных уравнений, создать компьютерные модели и решить достаточно широкий круг задач по физике [5, 8, 9]. Для этого соответствующие диффуравнения представляются в конечно-разностном виде [3–7] и создается макрос (небольшая программа) на языке Visual Basic [1, 2, 10]. Для написания макроса достаточно выбрать: Вид –> Панели инструментов –> Элементы управления –> Кнопка. Необходимо кнопку Command Button1 перенести на таблицу и дважды кликнуть по ней. В появившееся окно следует записать текст программы, которая будет исполняться после запуска. Макрос, произведя расчеты, создает таблицу результатов вычислений, на основе которых стандартными средствами Excel можно построить график изучаемой зависимости [1, 2, 8–10].
2. Теория используемого метода
Рассмотрим материальную точку, движущуюся в центральном поле с потенциальной энергией U=U(r), которая зависит только от расстояния r до центра O. Если это поле притяжения, то на нее действует сила F=F(r), направленная к O (рис. 1.1). Из законов механики следует:
Программа для расчета движения частицы содержит цикл, в котором пересчитываются проекции действующей силы, ускорения, скорости, координаты в последовательные моменты времени t и строится траектория.
На рис 1.2 представлен результат моделирования движения частицы в поле гравитационных сил притяжения, действующих по закону обратных квадратов; траекторией является эллипс. Из рис. 2.1 видно, что при малых скоростях точка движется по эллиптической орбите (траектории 1, 2, 3, 4), а при больших – по гиперболе (траектории 5, 6). Критическому случаю соответствует параболическая траектория. На рис. 2.2 представлены результаты расчетов движения частицы в центральном поле, для которого сила не подчиняется закону обратных квадратов. Видно, что траекторией является незамкнутая кривая (розетка). По теореме Бертрана, частица движется по замкнутой траектории в двух случаях: 1) в поле квазиупругой силы (F пропорциональна r); 2) в поле силы притяжения, которая обратно пропорциональна квадрату расстояния r до центра O.
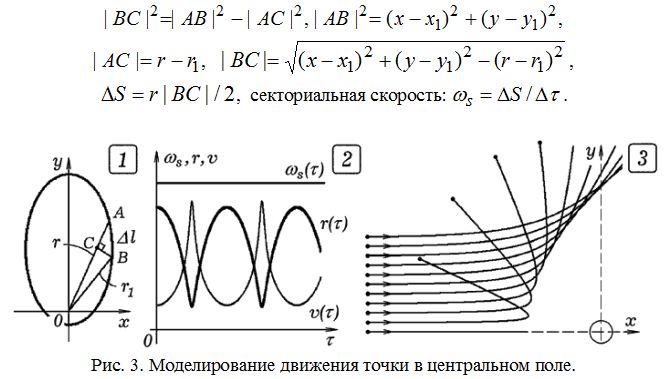
По второму закону Кеплера секториальная скорость планеты остается постоянной. Определить секториальную скорость можно следующим образом. Пусть за время dt планета перемещается из A(x,y) в B(x1,y1) (рис. 3.1). Из геометрических соображений:
Радиус–вектор планеты заметает площадь треугольника OAB. Из рис. 3.2 представлены графики зависимости от времени расстояния r от планеты до Солнца, модуля линейной скорости v и секториальной скорости. Видно, что секториальная скорость не изменяется, это и подтверждает второй закон Кеплера.
При движении частицы в поле сил отталкивания, подчиняющейся закону обратных квадратов, она движется по гиперболической траектории. На рис. 3.3 представлены результаты расчетов движения альфа–частиц в поле положительно заряженного ядра атома (опыт Резерфорда) при различных значениях прицельного параметра (начальной координаты y0).
3. Порядок выполнения работы
1. Изучите теорию движения точки в центрально симметричном поле сил притяжения и отталкивания. Запишите теорему Бертрана и законы Кеплера. По каким траекториям может двигаться точка? В каком случае траектория замкнута?
2. Изучите математическую модель явления и алгоритм, позволяющий рассчитать движение точки в поле центральной силы.
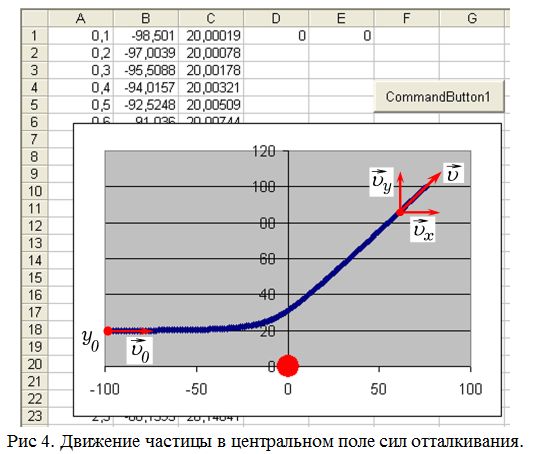
3. По направлению к массивному положительно заряженному ядру движутся альфа–частицы (опыт Резерфорда). Рассчитайте траекторию движения альфа–частиц в Excel. Для этого наберите и запустите программу ПР–1. В начале программы следует задать прицельный параметр y0 = 30. Действуют силы отталкивания, поэтому в программе сила F положительна. Траекториями частиц являются гиперболы (рис. 4). Все физические величины измеряются в условных единицах.
4. В опыте Резерфорда определялись вероятности отклонения альфа-частиц ядрами атомов золота на различные углы. Дополните программу так, чтобы она вычисляла угол отклонения направления движения частицы после взаимодействия. Если активизировать оператор Cells(i / 100, 4) = vy /vx, то после запуска программы в столбце D появится тангенс угла между составляющими вектора скорости (рис. 4). Чтобы получить значение угла в градусах, в ячейку E1 записывают “=ATAN(D1)*180/3,1415”, а затем копируют эту формулу в остальные ячейки столбца E.
5. Проведите серию вычислительных экспериментов при различных прицельных параметрах y0=0, 1, 2, 3, 5, 10, 15, 20, 25 и т.д., каждый раз правильно определяя угол отклонения частицы и записывая результат в таблицу Excel. По полученным данным постройте график зависимости угла отклонения от прицельного параметра.
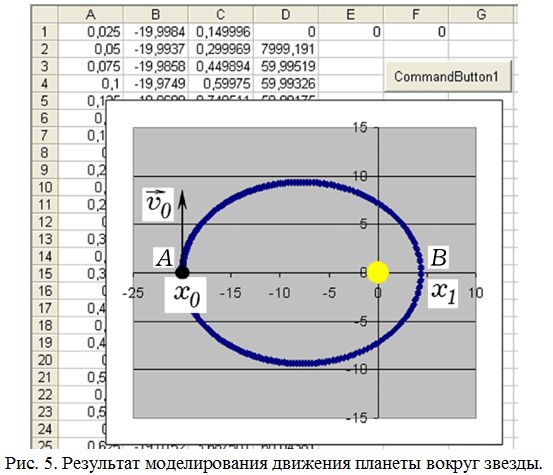
6. Промоделируйте движение планеты вокруг Солнца (рис. 5). Для этого наберите программу ПР–2 и запустите ее. Повторите моделирование при других начальных координатах и скоростях планеты. Убедитесь, что при малых скоростях планета движется по замкнутой эллиптической орбите. При увеличении начальной скорости эллипс становится более вытянутым, превращается в параболу (критический случай), а затем в гиперболу.
7. Изучите метод определения секториальной скорости планеты через площадь треугольника ОАВ (рис. 3.1). Активизируйте закомментированные операторы, которые вычисляют секториальную скорость планеты в различные моменты времени и выводят ее в столбец D. Убедитесь в том, что секториальная скорость планеты остается постоянной (второй закон Кеплера).
8. Предложите способ проверки третьего закона Кеплера, из которого следует, что отношение квадрата периода обращения к кубу большой полуоси ее орбиты для любой планеты остается постоянным. Для этого необходимо промоделировать движение планеты при различных ее начальных координатах и скоростях, определить период ее обращения и большую полуось орбиты. Если начальные условия задать так: x0=–20, y0=0, vx=0, vy=6 (все величины в условных единицах), то планета начнет свое движение из точки А(x0,0) , лежащей на оси Ox левее нуля, со скоростью, параллельной оси Oy. Через половину периода t1=T/2 она оказывается в точке B(x1,0). Большая ось AB эллипса имеет длину x1–x0 и совпадает с осью Ox. Поэтому большая полуось орбиты a=(x1-x0)/2. Значение x1 и соответствующий ему момент времени t1 могут быть найдены из таблицы, получающейся в результате работы программы ПР–2. Период обращения планеты T=2*t1.
9. Выполните 5–8 численных экспериментов при различных начальных координатах x и скоростях vy и заполните таблицу. Убедитесь, что во всех случаях коэффициент k, равный отношению квадрата периода к кубу большой полуоси орбиты остается постоянным. Пример таблицы приведен ниже.
9. Несколько (3 – 6) раз промоделируйте движение планеты при одинаковых x0 и различных vy, в каждом случае определяя большую полуось a=(x1-x0)/2 орбиты, перигелийное расстояние q (оно равно | x0 | или x1) и эксцентриситет e=1-q/a. Результаты оформите в виде таблицы.
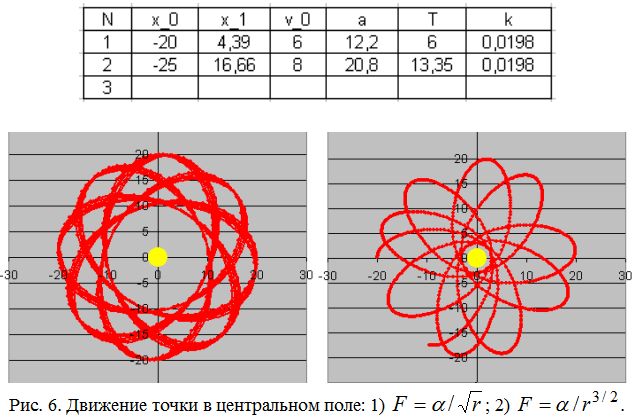
10. Промоделируйте движение точки в поле центральной силы притяжения, не подчиняющейся закону обратных квадратов (рис. 6).
11. Измените программу так, чтобы она моделировала движение частицы в центральном поле силы
Коэффициенты в формуле следует подобрать так, чтобы при больших r преобладали силы притяжения, а при малых – силы отталкивания. Аналогичное уравнение описывает силу взаимодействия между атомами. Получающиеся траектории (рис. 7) зарисуйте в тетрадь.
12. В выводе охарактеризуйте и объясните полученные результаты.
4. Заключение
В статье представлена методика использования электронных таблиц MS Excel для моделирования движения материальной точки в поле центральных сил притяжения и отталкивания. Предложена инструкция к лабораторной работе, которая может быть проведена в компьютерном классе. Рассмотренные программы позволяют: 1) рассчитать движение планет вокруг звезды; 2) промоделировать движение частицы в гравитационном поле по эллиптической, параболической и гиперболической траектории; 3) подтвердить второй и третий законы Кеплера; 4) промоделировать отклонение альфа-частиц в поле отталкивания ядра атома; 5) промоделировать движение частицы в поле силы, не подчиняющейся закону обратных квадратов. Установлено, что для моделирования перечисленных выше явлений достаточно создать два небольших макроса на языке Visual Basic. Использование предложенной лабораторной работы на занятиях по компьютерному моделированию способствует установлению межпредметных связей между математикой, физикой, информатикой, астрономией и повышению интереса к этим дисциплинам.
Библиографический список
- Васильев А.Н. Научные вычисления в Microsoft Excel. – М.: Издательский дом “Вильямс”, 2004.– 512 с.
- Гельман В.Я. Решение математических задач средствами Excel: Практикум. – СПб.: Питер, 2003. – 240 с.
- Майер Р.В. Задачи, алгоритмы, программы [Электронный ресурс] / Глазов: ГГПИ, 2011. URL: http://maier–rv.glazov. net (http://mayer.hop.ru )
- Майер Р.В. Компьютерное моделирование физических явлений. –– Глазов, ГГПИ: 2009. –– 112 с. (http://maier–rv.glazov.net )
- Майер Р.В. Решение физических задач с помощью электронных таблиц MS Excel // International Journal of Open Information Technologies — vol. 2, – no. 9, – 2014. – С. 18-23.
- Могилев А.В. Информатика: Учеб пособие для студ. пед. вузов / А.В. Могилев, Н.И.Пак, Е.К.Хеннер. – М.: Издательский центр “Академия”, 2003. – 816 с. (C. 711–714)
- Самарский А.А. Математическое моделирование: Идеи. Методы. Примеры /А.А.Самарский, А.П.Михайлов. – М.: Физматлит, 2001.– 320 с.
- Старовиков М.И. Введение в экспериментальную физику: Учебное пособие. – Спб.: Издательство “Лань”, 2008. – 240 с.
- Угринович Н.Д. Исследование информационных моделей. Элективный курс: Учебное пособие. – М.: БИНОМ. Лаборатория знаний, 2004. – 183 с.
- Уокенбах Д. Профессиональное программирование на VBA в Excel 2002. – Москва, Санкт-Петрбург, Киев: 2003. – 781 с.
Количество просмотров публикации: Please wait