В задачах прямого проектирования [1,2], оптимального проектирования [3,4,5] или в задачах моделирования работы сооружений [6,7,8] целесообразно использовать наиболее рациональные или оптимальные (не оптимизируемые в данной конкретной задаче) параметры элементов строительных конструкций. В связи с этим желательно иметь ряд формул для назначения этих параметров. В данной работе приведен вывод формул для одно из случаев сечений элементов – прямоугольного бруса.
Рассмотрим задачу оптимизации сечения бруса прямоугольного сечения, подверженного косому изгибу (рис. 1).
Требуется запроектировать брус минимальной площади поперечного сечения так, чтобы напряжения не превосходили расчетного сопротивления.
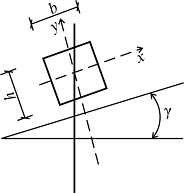
Рис. 1. Оптимизация сечения прямоугольного бруса
Площадь сечения бруса
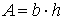 .
.Расчетное сопротивление при косом изгибе
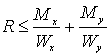 .
.Примем за неизвестные оптимизационной задачи моменты сопротивления сечения Wx и Wy, которые обозначим х2/6 и х1/6 соответственно. Тогда площадь поперечного сечения будет представлена зависимостью
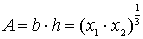 .
.найти min
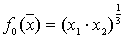
при
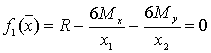 .
.Функции f0 и f1
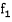 и их частные производные непрерывны при хk > 0. Значит, по теореме Вейерштрасса, решение существует.
и их частные производные непрерывны при хk > 0. Значит, по теореме Вейерштрасса, решение существует.2. Применение принципа Лагранжа.
Функция Лагранжа
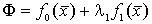
или
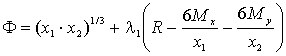 .
.Необходимые условия экстремальности:
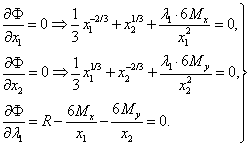
Перенесем члены, содержащие λ1 в первых двух уравнениях в правую часть:
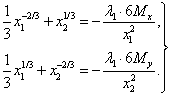
Поделим первое уравнение на второе
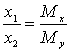 ,
,или
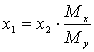 .
.Подставим это выражение в третье уравнение системы
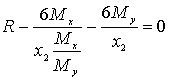 ,
,или
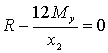 ,
,откуда
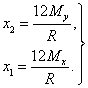
Стационарная точка единственная, значит, она является решением задачи.
Перейдем к переменным b и h, то есть к размерам сечения
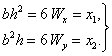
или
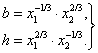
Библиографический список
- Шеин А.И., Завьялова О.Б. РАСЧЕТ МОНОЛИТНЫХ ЖЕЛЕЗОБЕТОННЫХ КАРКАСОВ С УЧЕТОМ ПОСЛЕДОВАТЕЛЬНОСТИ ВОЗВЕДЕНИЯ, ФИЗИЧЕСКОЙ НЕЛИНЕЙНОСТИ И ПОЛЗУЧЕСТИ БЕТОНА
Строительная механика и расчет сооружений. 2012. № 5. С. 64-69. - Шеин А. И. РЕШЕНИЕ МНОГОПАРАМЕТРИЧЕСКОЙ ЗАДАЧИ ДННАМИКИ СТЕРЖНЕВЫХ СИСТЕМ МЕТОДОМ СЕТОЧНОЙ АППРОКСИМАЦИИ ЭЛЕМЕНТОВ
Промышленное и гражданское строительство. 2002. № 2. С. 27. - Шеин А.И., Земцова О.Г. ОПТИМИЗАЦИЯ МНОГОМАССОВЫХ ГАСИТЕЛЕЙ КОЛЕБАНИЙ ПРИ ГАРМОНИЧЕСКОМ ВОЗДЕЙСТВИИ
Известия высших учебных заведений. Поволжский регион. Технические науки. 2010. № 1. С. 113-122. - Шеин А.И., Шмелев Д.А. ОЦЕНКА ЭФФЕКТИВНОСТИ АКТИВНОГО ЖИДКОСТНОГО ГАСИТЕЛЯ КОЛЕБАНИЙ ВЫСОТНЫХ СООРУЖЕНИЙ ПРИ НЕСТАЦИОНАРНЫХ ВОЗДЕЙСТВИЯХ.
Строительная механика и расчет сооружений. 2014. № 1 (252). С. 59-63. - Шеин А.И., Земцова О.Г. СНИЖЕНИЕ УРОВНЯ КОЛЕБАНИЙ СИСТЕМЫ «УПРУГОЕ ОСНОВАНИЕ – ВЫСОТНОЕ СООРУЖЕНИЕ» С ПОМОЩЬЮ НЕЛИНЕЙНОГО ДИНАМИЧЕСКОГО ГАСИТЕЛЯ
Региональная архитектура и строительство. 2011. № 2. С. 83-90. - Шеин А.И., Земцова О.Г. СХЕМЫ И ТЕОРИЯ ГАСИТЕЛЕЙ ПРОСТРАНСТВЕННЫХ КОЛЕБАНИЙ СООРУЖЕНИЙ
Региональная архитектура и строительство. 2010. № 1. С. 45-52. - Шеин А.И., Зайцев М.Б.
МЕТОД СМЕЩЕННЫХ РАЗНОСТЕЙ ДЛЯ РЕШЕНИЯ СИСТЕМ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ДВИЖЕНИЯ МЕХАНИЧЕСКИХ СИСТЕМ
Строительная механика и расчет сооружений. 2012. № 2. С. 38-41. - Шеин А.И., Шмелёв Д.А. ПОСТРОЕНИЕ И РЕАЛИЗАЦИЯ МАТЕМАТИЧЕСКОЙ МОДЕЛИ ГАШЕНИЯ КОЛЕБАНИЙ ВЫСОТНЫХ ЗДАНИЙ С ПОМОЩЬЮ РЕАКТИВНЫХ ГАСИТЕЛЕЙ
Региональная архитектура и строительство. 2014. № 1. С. 96-103.
Количество просмотров публикации: Please wait


