Задачи на построение дескриптивных моделей на языке математики (математическое моделирование) – яркий пример задач, которые практически невозможно решить без применения компьютеров.
В школьном курсе информатики обучение компьютерному математическому моделированию направлено на решение задач на разработку моделей прогноза (задачи типа «Что будет, если…?» или «Что будет через какое-то время…?») и оптимизации (задачи типа «Как сделать, чтобы…?»). В качестве среды для реализации и исследования математических моделей используется табличный процессор. Программы данного класса дают возможность без изучения языков программирования выполнять расчеты по сложным формулам.
Среди задач математического моделирования для школьников представляют интерес задачи на построение регрессионных моделей. Как указывает Ю.П. Штепа, при построении регрессионных моделей сам процесс получения модели является почти полностью автоматизированным. А вот для исследования модели необходимо уметь выдвигать гипотезы, оценивать адекватность и непротиворечивость модели, выбирать наиболее подходящую модель, не бездумно доверяя компьютеру, а проявляя критичность мышления, способности к оценочным суждениям, видению проблем и противоречий [1].
Рассмотрим пример решения одной из задач.
Как известно, скорость автомобиля зависит от количества лошадиных сил (л.с.) в его двигателе. Используя следующие данные (Табл. 1), определите максимальную скорость движения следующих автомобилей, согласно мощности их двигателя: «Пежо-307» – 101.л.с.; «Рено-Меган» – 107 л.с.; «Форд» – 120 л.с.
Таблица 1
|
Название машины |
Мощность двигателя, л.с. |
Максимальная скорость (км/ч) |
| Запорожец |
55 |
120 |
| Жигули |
62 |
140 |
| Москвич |
67 |
147 |
| Лада |
75 |
165 |
| Хантер |
87 |
184 |
| Тойота Виста |
96 |
190 |
Цель моделирования – построить модель расчета максимальной скорости автомобиля в зависимости от количества лошадиных сил в его двигателе. Объект моделирования – автомобиль, характеризующийся двумя параметрами: максимальной скоростью и мощностью двигателя. Будем считать, что влияние не упомянутых в задаче факторов незначимо.
| Объект | Параметры | Вид параметров | Обозначение |
| Автомобиль | Максимальная скорость автомобиля | Исходные данные | V |
| Мощность двигателя (в л.с.) | Исходные данные | M | |
| Скорость автомобиля в зависимости от мощности двигателя | Результат | V(М) |
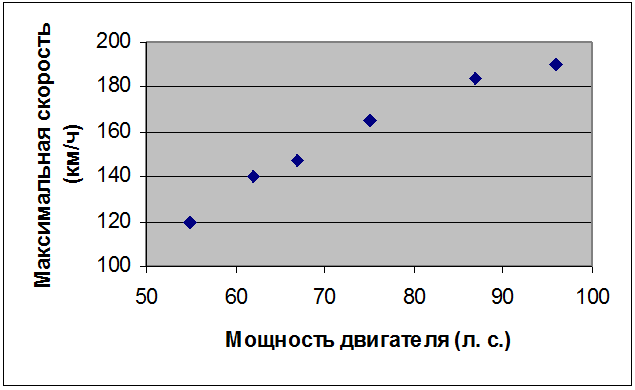
Для удобства решения объединим формализованное описание объекта и разработку компьютерной модели в один этап. Построим график зависимости максимальной скорости автомобиля от мощности двигателя по известным данным (рис.1).
Рис. 1
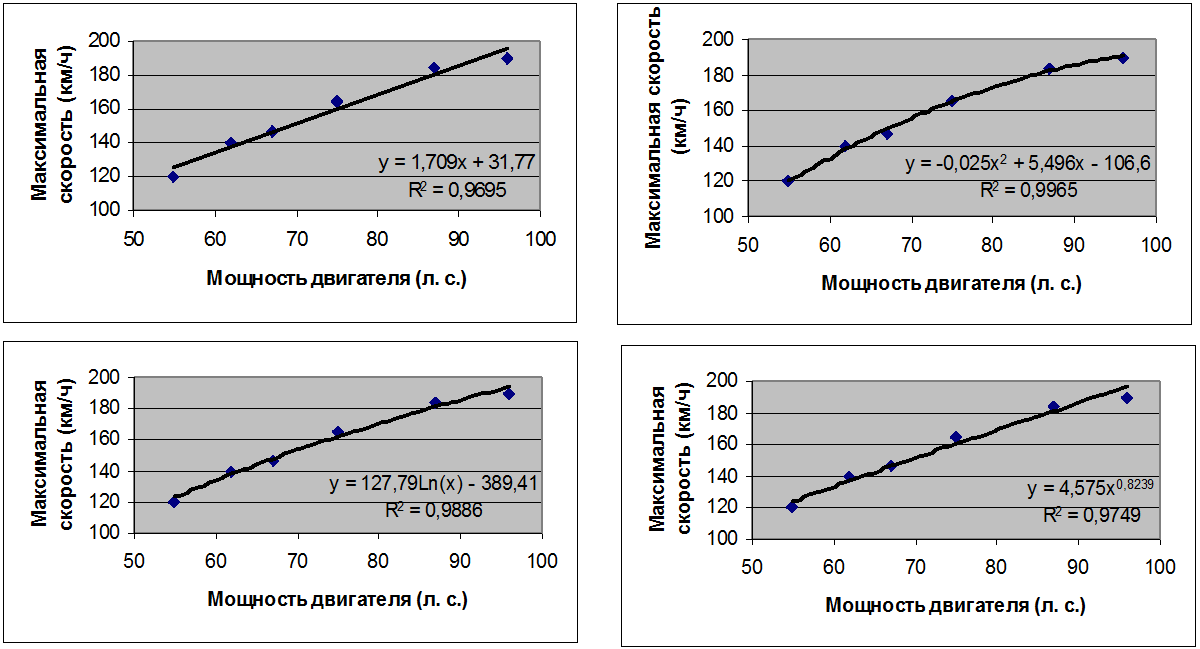
Учитывая расположение точек на диаграмме, при построении регрессионной модели произведем выбор из следующих видов функций: линейная, квадратичная, логарифмическая и степенная. Построим соответствующие тренды (рис. 2).
Рис. 2
Мы получили четыре возможных варианта регрессионной модели. Все тренды практически полностью проходят через экспериментальные точки. Поэтому для выявления наиболее подходящей функции обратим внимание на размер критерия R2 (коэффициент детерминированности).
Значение R2 наибольшее у квадратичной функции, оно очень близко к единице. Это говорит о том, что данная модель является почти идеальной. Поэтому дальнейшие расчеты произведем, подставляя значения мощности двигателя автомобилей «Пежо», «Рено-Меган» и «Форд» в качестве аргумента функции y = –0,025x2 + 5,496x – 106,6. Получим следующую таблицу значений:
| Мощность двигателя (л.с.) |
101 |
107 |
120 |
| Максимальная скорость (км/ч) |
193 |
195 |
193 |
Данный результат свидетельствует о последующем снижении величины максимальной скорости автомобиля в зависимости от мощности двигателя (график полученной квадратичной функции – парабола, ветви которой направлены вниз). Учитывая, что увеличение мощности двигателя объективно влечет за собой и увеличение максимальной скорости автомобиля, полученная регрессионная модель противоречит реальности и ее нельзя считать адекватной. Это подтверждает тот факт, что за пределами экспериментальной области характер функции может существенно меняться, и экстраполяция может давать неправдоподобные результаты. Так, например, для мощности двигателя 200 л.с. мы вообще получаем отрицательную величину скорости.
Для получения более правдоподобной модели выберем логарифмическую функцию – из оставшихся функций ее коэффициент детерминированности – наибольший. Получим следующую таблицу значений:
| Мощность двигателя (л.с.) |
101 |
107 |
120 |
| Максимальная скорость (км/ч) |
200 |
208 |
222 |
Полученные значения являются более достоверными и такую модель вполне можно считать адекватной и непротиворечивой.
Для закрепления умений решать задачи регрессионного прогнозирования можно использовать следующие задачи:
1. Иван начал заниматься футболом в первом классе. Родители Ивана в течение нескольких лет фиксировали, сколько времени тратил сын на занятия футболом.
| Класс |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
| Кол-во часов |
314 |
448 |
518 |
532 |
574 |
606 |
638 |
698 |
717 |
В этом году Иван окончил 9 классов и собирается поступать в колледж и продолжать заниматься футболом. Необходимо спрогнозировать количество часов, которое будет затрачено Иваном на тренировки в годы учебы в колледже.
2. Средняя зарплата учителя за последние полгода изменялась следующим образом:
| Месяц | Январь | Февраль | Март | Апрель | Май | Июнь | |
| Размер зарплаты | 17317 | 17750 | 18600 | 18650 | 19000 | 19113 | |
Составьте прогноз о размере зарплаты учителя на следующие 3 месяца.
3. В 2006 году Григорий Шоев решил открыть акционерное общество «Григорий &Ko». В таблице приведены данные о средней цене акций этого предприятия в разные годы.
| Год | 2006 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 |
| Стоимость (руб.) | 12 | 20 | 15 | 26 | 38 | 45 | 66 | 78 |
Спрогнозируйте стоимость акций на ближайшие пять лет.
4. В таблице приведены данные о зависимости количества источников, которые были задействованы в подготовке сочинения, и количестве баллов, полученных за данные сочинения по 100-балльной системе:
| Фамилия |
Количество источников |
Количество баллов |
| Сидоров |
3 |
35 |
| Петров |
4 |
39 |
| Иванов |
21 |
67 |
| Козлов |
11 |
47 |
| Ненашев |
6 |
44 |
| Козев |
20 |
62 |
| Ушков |
13 |
55 |
| Гринштейн |
25 |
79 |
Сделайте прогноз о количестве баллов за сочинение для следующих учащихся в соответствии с количеством используемых ими источников литературы: Перов – 27; Мамыкин – 23; Ерофеев – 9 источников.
5. Статистические данные указывают на то, что средний балл успеваемости в школе зависит от количества часов, которые ученик ежедневно проводит за обучением дома. Это можно увидеть из следующей таблицы:
|
Фамилия |
Количество часов |
Средний балл |
| Сидоров |
0 |
2 |
| Петров |
0,5 |
2,8 |
| Иванов |
1,6 |
3,0 |
| Козлов |
2 |
3,2 |
| Ненашев |
3,1 |
3,6 |
| Козев |
3,5 |
4 |
| Ушков |
4,2 |
4,3 |
| Гринштейн |
4,5 |
4,8 |
Произведите прогноз среднего балла успеваемости для следующих учеников в соответствии с затрачиваемым ими временем: Волков – 4 часа; Петухов – 2,5 часа; Зайцев – 5,5 часов.
Большое количество задач по данной теме содержится в работах Ю.П. Штепы [2-5].
В заключение отметим, что знания и умения, полученные учащимися в процессе решения «несерьезных» задач информационного моделирования в школе, являются базисом для создания в будущем моделей гораздо более высокого уровня сложности, таких как, например, модели, разработанные студентами и описанные в статьях [6-7].
Библиографический список
- Штепа Ю.П. Методика обучения старшеклассников решению задач по информационному моделированию в контексте новых образовательных результатов: монография. – Биробиджан: Изд-во ДВГСГА, 2010. 101 с.
- Штепа Ю.П. Решение задач прогнозирования и оптимизации в школьном курсе информатики // Информатика и образование. 2008. № 9. С. 37-48.
- Штепа Ю.П. Решение задач прогнозирования и оптимизации в школьном курсе информатики // Информатика и образование. 2008. № 10. С. 39-47.
- Штепа Ю.П. Решение задач прогнозирования и оптимизации в школьном курсе информатики // Информатика и образование. 2008. № 11. С. 39-50.
- Штепа Ю.П. Информационное моделирование: сборник задач. – Биробиджан: Изд-во ДВГСГА, 2008. 64 с.
- Баженов Р. И., Афанасьева М. А. Разработка программной модели контроля дверей холодильника на основе теории автоматов // Журнал научных публикаций аспирантов и докторантов. 2014. №4(94). С. 306-308.
- Баженов Р.И., Лопатин Д.К. Об имитационном моделировании экономических процессов средствами специализированной программной среды // Молодой ученый. 2014. № 4. С. 88-92.
Количество просмотров публикации: Please wait