Задачи, связанные с акустическим зондированием пористых сред с целью определения характеристик насыщающих флюидов или протяженности нефтеносных и газоносных пластов, а также использование пористых материалов для шумоизоляции и теплоизоляции, актуализируют теоретические и экспериментальные исследования, связанные с прохождением и поглощением звука в пористых средах, насыщенных жидкостью или газом.
Так, например, в работе [1] исследуются волновые процессы во влажных, насыщенных парогазовой смесью пористых средах с учетом межфазных сил взаимодействия, тепло- и массообмена между скелетом пористой среды, жидкостью и парогазовой смеси. Получены дисперсионные соотношения для случаев насыщения пористой среды парогазовой смесью, паром или газом. Показано, что повышение температуры парогазовой смеси в пористой среде приводит к уменьшению коэффициента затухания «быстрой» волны из-за уменьшения плотности парогазовой смеси и, как следствие, уменьшения влияния межфазных сил.
Обзор некоторых других работ [2-11], посвященных изучению процессов, связанных с распространением звуковых волн в насыщенных пористых материалах, проведен в [12].
Во многих случаях пористые среды могут представлять собой слои, разделенные открытой или закрытой границами. Тип границы существенно влияет на результат прохождения и отражения акустического сигнала. Поэтому подбором открытых или закрытых границ можно получить акустическую перегородку с требуемыми свойствами.
В данной работе рассмотрена задача об отражении и прохождении акустического сигнала через закрытые границы пористой среды, а также рассмотрены комбинации открытой и закрытой границ. Процессы, происходящие на открытой границе раздела однородной и пористой сред, также рассмотрены в работе [12].
Система макроскопических уравнений масс и импульсов для рассматриваемой системы в целом и для газовой фазы имеет вид, аналогичный системе, описанной в работах [2, 7]. При расчетах используются предположения и дисперсионное соотношение, записанные в работе [2].
Рассмотрим насыщенную газом пористую среду, ограниченную двумя параллельными плоскостями, отстоящими друг от друга на расстоянии  , и перпендикулярными выбранному направлению
, и перпендикулярными выбранному направлению 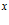 (рис. 1). Расстояние
(рис. 1). Расстояние  назовем толщиной пористой среды (перегородки); высоту и ширину пористой среды будем считать достаточно большими, чтобы пренебречь краевыми эффектами. Как и в работе [12], будем рассматривать случаи, когда падающая волна перпендикулярна к плоскости падения.
назовем толщиной пористой среды (перегородки); высоту и ширину пористой среды будем считать достаточно большими, чтобы пренебречь краевыми эффектами. Как и в работе [12], будем рассматривать случаи, когда падающая волна перпендикулярна к плоскости падения.
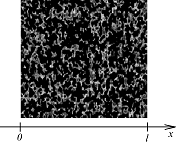
Рисунок 1 – Схема расположения пористой перегородки в однородной среде
Пусть плоская гармоническая волна падает на первую границу 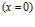 раздела однородной и пористой сред, причем границы пористой перегородки покрыты тонкой непроницаемой пленкой. Движение в левой части от пористой среды (
раздела однородной и пористой сред, причем границы пористой перегородки покрыты тонкой непроницаемой пленкой. Движение в левой части от пористой среды (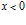 ) является наложением двух волн – падающей:
) является наложением двух волн – падающей:
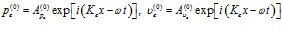 (1)
(1)
и отраженной:
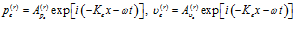 , (2)
, (2)
где 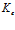 – волновое число для внешней однородной среды,
– волновое число для внешней однородной среды, 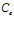 – фазовая скорость волны во внешней среде. Нижний индекс
– фазовая скорость волны во внешней среде. Нижний индекс 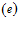 здесь и далее будем относить к параметрам среды, окружающей пористую перегородку. Амплитуды давлений и скоростей в однородной среде связаны соотношениями:
здесь и далее будем относить к параметрам среды, окружающей пористую перегородку. Амплитуды давлений и скоростей в однородной среде связаны соотношениями:
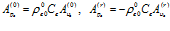 . (3)
. (3)
Прошедшая через первую границу волна делится на две: одна волна распространяется по газу в порах:
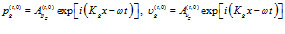 , (4)
, (4)
другая – по скелету пористой среды:
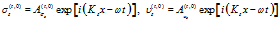 . (5)
. (5)
Условия равенства давлений и скоростей на первой границе имеют вид:
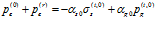 , (6)
, (6)
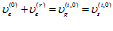 . (7)
. (7)
Рассмотрим теперь прохождение волн через вторую границу 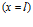 . В этом случае движение слева от второй границы (
. В этом случае движение слева от второй границы (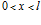 ) как в газовой фазе, так и в скелете, является наложением двух волн – падающей (соответственно (4) и (5)) и отраженной:
) как в газовой фазе, так и в скелете, является наложением двух волн – падающей (соответственно (4) и (5)) и отраженной:
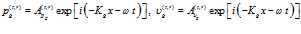 , (8)
, (8)
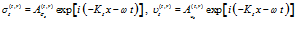 . (9)
. (9)
В правой части от второй границы (в области 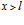 ) распространяется одна волна, являющаяся результирующей волн, вышедших из газовой фазы:
) распространяется одна волна, являющаяся результирующей волн, вышедших из газовой фазы:
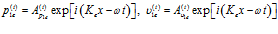 , (10)
, (10)
и из скелета среды:
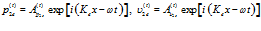 . (11)
. (11)
Отметим, что для (10) и (11) соотношения (3) также справедливы. Условия равенства давлений и скоростей на второй границе запишем в следующем виде:
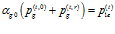 ,
, 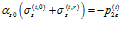 , (12)
, (12)
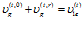 ,
, 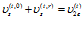 . (13)
. (13)
Найдем коэффициенты отражения 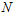 и прохождения
и прохождения 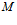 волн, определяемые соответственно как отношения давлений отраженной волны к падающей волне и прошедшей волны к падающей волне. Исходя из граничных условий (6) и (7), после соответствующих выкладок и преобразований, для первой границы получим следующие коэффициенты отражения и прохождения:
волн, определяемые соответственно как отношения давлений отраженной волны к падающей волне и прошедшей волны к падающей волне. Исходя из граничных условий (6) и (7), после соответствующих выкладок и преобразований, для первой границы получим следующие коэффициенты отражения и прохождения:
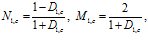 (14)
(14)
где 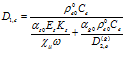 ,
, 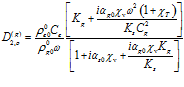 ,
, 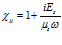 . Коэффициенты
. Коэффициенты 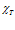 и
и 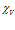 определяют влияние межфазного теплообмена и межфазных сил [2, 7]. Дополнительный нижний индекс
определяют влияние межфазного теплообмена и межфазных сил [2, 7]. Дополнительный нижний индекс 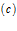 соответствует «закрытой» границе пористой среды, а нижний индекс
соответствует «закрытой» границе пористой среды, а нижний индекс 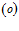 – «открытой» границе.
– «открытой» границе.
На второй границе:
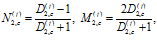 (15)
(15)
где 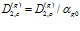 ,
, 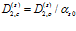 ,
, 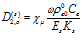 .
.
Верхний индекс 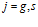 , заключенный в скобки, соответствует газовой фазе и скелету среды соответственно.
, заключенный в скобки, соответствует газовой фазе и скелету среды соответственно.
Для величины 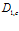 независимо от параметров внешней среды, учитывая слабую зависимость фазовой скорости от круговой частоты для пористой среды в случае
независимо от параметров внешней среды, учитывая слабую зависимость фазовой скорости от круговой частоты для пористой среды в случае 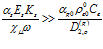 , получаем:
, получаем: 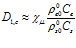 . Кроме того, если выполнено условие
. Кроме того, если выполнено условие 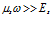 , то
, то 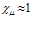 и поэтому
и поэтому 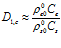 . Таким образом, когда поверхность пористой среды покрыта тонкой непроницаемой пленкой, коэффициенты отражения и прохождения волн для первой границы зависят только от отношений волновых сопротивлений сред. В тех случаях, когда
. Таким образом, когда поверхность пористой среды покрыта тонкой непроницаемой пленкой, коэффициенты отражения и прохождения волн для первой границы зависят только от отношений волновых сопротивлений сред. В тех случаях, когда 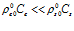 (что имеет место, когда окружающая однородная среда – газ), получаем:
(что имеет место, когда окружающая однородная среда – газ), получаем: 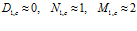 . Это означает, что в случае «закрытой» границы стенка пористой перегородки представляет собой абсолютно жесткую поверхность.
. Это означает, что в случае «закрытой» границы стенка пористой перегородки представляет собой абсолютно жесткую поверхность.
Отмечу также, что наличие непроницаемой пленки на первой границе приводит к тому, что по насыщаемому поры газу распространяется волна незначительной амплитуды (по сравнению с амплитудой волны, распространяющейся по скелету пористой перегородки):
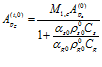 . (16)
. (16)
Это связано с тем, что скелет пористой среды значительно «жестче» насыщающего его газа, и при наличии жесткой непроницаемой пленки именно он воспринимает основную часть энергии падающей на первую границу волны.
При больших значениях круговой частоты и 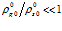 на второй границе получим:
на второй границе получим: 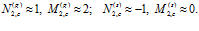 Таким образом, в случае «закрытой» границы для волны, распространяющейся по газу в порах, вторая граница представляет собой абсолютно жесткую поверхность, а для волны, распространяющейся по скелету пористой перегородки, – абсолютно мягкую поверхность.
Таким образом, в случае «закрытой» границы для волны, распространяющейся по газу в порах, вторая граница представляет собой абсолютно жесткую поверхность, а для волны, распространяющейся по скелету пористой перегородки, – абсолютно мягкую поверхность.
На основе полученных выражений (14) и (15) для коэффициентов отражения и прохождения на границах пористой среды, рассмотрим динамику волны конечной длительности при прохождении через пористую перегородку.
Будем рассматривать импульсы давлений, временная протяженность которых удовлетворяет следующему условию: 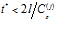 . Выполнение этого условия позволяет нам не учитывать влияние отраженного от противоположной границы импульса на прохождение импульсом рассматриваемой границы, и наоборот.
. Выполнение этого условия позволяет нам не учитывать влияние отраженного от противоположной границы импульса на прохождение импульсом рассматриваемой границы, и наоборот.
Пусть с левой стороны на границу раздела однородной и пористой сред (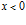 ) падает импульс давления, который имеет колоколообразную форму и описывается выражением
) падает импульс давления, который имеет колоколообразную форму и описывается выражением
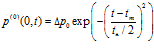 .
.
Здесь 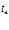 и
и 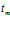 определяют характерную протяженность импульса, и момент времени, на который приходится максимум амплитуды первоначального импульса;
определяют характерную протяженность импульса, и момент времени, на который приходится максимум амплитуды первоначального импульса; 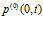 – осциллограмма давления для падающей волны. Отраженный и прошедший сигналы, используя преобразование Фурье, запишем в виде:
– осциллограмма давления для падающей волны. Отраженный и прошедший сигналы, используя преобразование Фурье, запишем в виде:
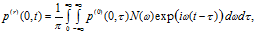
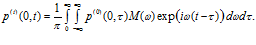
На рис. 2 представлена схема расположения датчиков, фиксирующих импульсы давлений в пористой среде при прохождении волн. Датчик D1 размещен с левой стороны, вблизи первой границы пористой среды и регистрирует исходный импульс давления и отраженный. Датчики D2 и D3 расположены внутри пористой среды, вблизи первой границы и регистрируют прошедшие импульсы давлений в порах среды и материале скелета соответственно. Датчики D4 и D5 расположены внутри пористой среды, вблизи второй границы и регистрируют импульсы, дошедшие до этой границы и отраженные от нее («медленная» и «быстрая» волны соответственно). Датчик D6 расположен справа от пористой среды, вблизи второй границы и регистрирует прошедшие через вторую границу импульсы давлений (по порам и по скелету).
Результаты численной реализации, полученные с использованием метода быстрого преобразования Фурье для эволюции импульса давления при взаимодействии с пористой перегородкой толщиной 1 м с «закрытыми» и «открытыми» границами представлены на рис. 3 – 6. Параметры фаз взяты при температуре среды 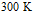 и давлении
и давлении 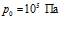 . Для резины:
. Для резины: 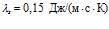 ,
, 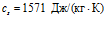 ,
, 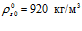 ,
, 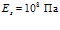 ,
, 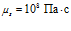 ; для воздуха:
; для воздуха: 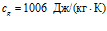 ,
, 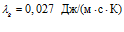 ,
, 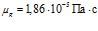 ,
, 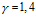 ,
, 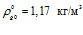 . Временная протяженность импульсного сигнала в расчетах равна
. Временная протяженность импульсного сигнала в расчетах равна 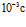 . Все расчеты проведены с учетом межфазных сил и теплообменных процессов.
. Все расчеты проведены с учетом межфазных сил и теплообменных процессов.
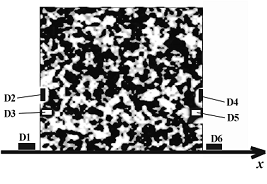
Рисунок 2 – Схема расположения датчиков, фиксирующих импульсы давлений в пористой среде при прохождении волн
На рис. 3 – 5 приведены расчетные осциллограммы, иллюстрирующие процессы отражения и прохождения, а также эволюцию волнового импульса в пористой среде толщиной 1 м с «закрытыми» границами. На рис. 6 первая граница «закрытая», а вторая «открытая» (толщина среды также 1 м). Штриховые линии соответствуют отраженной части импульса. В качестве однородной внешней среды на рис. 3 взят воздух, а на рис. 4 – 6 – вода; пористая среда насыщена воздухом. Линии 1 соответствуют импульсу, прошедшему вторую границу пористой среды по газу в порах, а линии 2 – прошедшему по скелету пористой среды. Характерные размеры среды: на рис. 3 и рис. 5 – 6 – 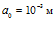 ,
, 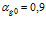 , на рис. 4 –
, на рис. 4 – 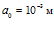 ,
, 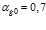 . Все расчеты проведены с учетом межфазных сил и теплообменных процессов.
. Все расчеты проведены с учетом межфазных сил и теплообменных процессов.
Из приведенных осциллограмм видно, что по газовой фазе распространяется незначительный импульс давления, что, как было отмечено выше, связано с тем, что в случае «закрытой» первой границы скелет пористой среды воспринимает основную часть энергии падающего на первую границу импульса.
Если пористая перегородка окружена воздухом (рис. 3), то она практически полностью экранирует исходный импульс (через вторую границу перегородки проходит лишь около 5% от исходного импульса). Из рис. 4 и рис. 5 ясно, что если в качестве однородной внешней среды выступает вода, то с увеличением содержания скелета увеличивается часть импульса, прошедшего вторую границу пористой перегородки. Изменение газосодержания пористой среды также влияет на процессы отражения и прохождения на первой границе перегородки – с увеличением газосодержания уменьшается часть импульса, проходящего по скелету пористой среды.
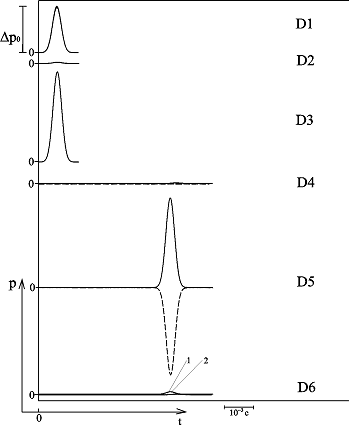
Рисунок 3 – Динамика отражения и прохождения импульсом давления «закрытых» границ пористой среды и эволюция импульса давления в пористой среде (характерные размеры среды: 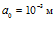 ,
, 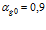 ; однородная внешняя среда – воздух)
; однородная внешняя среда – воздух)
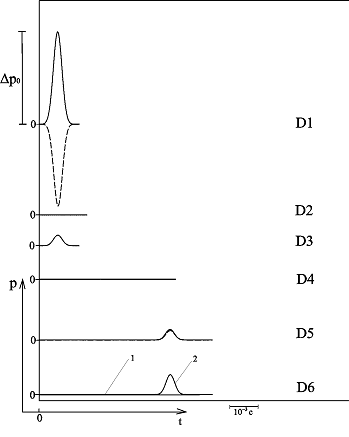
Рисунок 4 – Динамика отражения и прохождения импульсом давления «закрытых» границ пористой среды и эволюция импульса давления в пористой среде (характерные размеры среды: 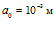 ,
, 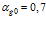 ; однородная внешняя среда – вода)
; однородная внешняя среда – вода)
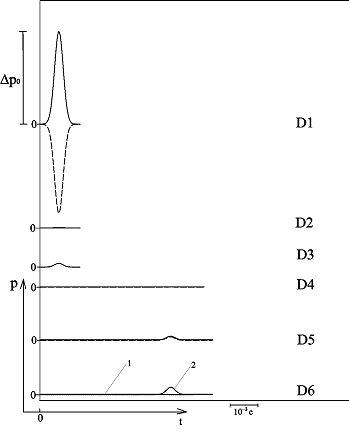
Рисунок 5 – Динамика отражения и прохождения импульсом давления «закрытых» границ пористой среды и эволюция импульса давления в пористой среде (характерные размеры среды: 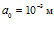 ,
, 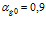 ; однородная внешняя среда – вода)
; однородная внешняя среда – вода)
На рис. 6 приведены расчетные осциллограммы для «закрытой» первой и «открытой» второй границ пористой перегородки толщиной 1 м, насыщенной воздухом, когда в качестве однородной внешней среды выступает вода.
В рамках представленных выше рассуждений и соотношений также можно рассмотреть случаи чередования пористых и однородных слоев (слои пористой среды обладают одинаковой пористостью, но насыщены разным флюидом; пористая среда насыщена одним и тем же флюидом, но пористость слоев среды различна).
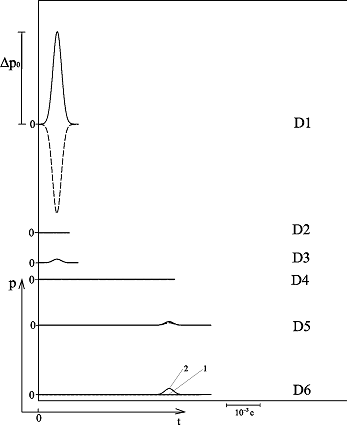
Рисунок 6 – Динамика отражения и прохождения импульсом давления «закрытой» первой и «открытой» второй границ пористой среды и эволюция импульса давления в пористой среде (характерные размеры среды: 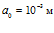 ,
, 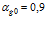 ; однородная внешняя среда – вода)
; однородная внешняя среда – вода)
Из представленных осциллограмм (рис. 3 – 6) видно, что по характеру вернувшегося импульса давления можно судить о свойствах флюидов, насыщающих пористую среду и о свойствах самой пористой среды, что позволяет акустическими методами исследовать параметры насыщенных пористых сред. Наличие непроницаемой пленки на первой границе приводит к тому, что по насыщаемому поры газу распространяется волна незначительной амплитуды (около 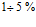 от амплитуды первоначального импульса). Кроме того, подбором соответствующей дисперсности пор среды, толщины перегородки, типа насыщающего пористую перегородку газа, и комбинируя «открытые» и «закрытые» границы, можно получить перегородку с требуемыми акустическими характеристиками.
от амплитуды первоначального импульса). Кроме того, подбором соответствующей дисперсности пор среды, толщины перегородки, типа насыщающего пористую перегородку газа, и комбинируя «открытые» и «закрытые» границы, можно получить перегородку с требуемыми акустическими характеристиками.
Библиографический список
-
Гималтдинов И.К., Дмитриев В.Л., Ситдикова Л.Ф. Динамика звуковых волн в насыщенных парогазовой смесью пористых средах // ТВТ. 2014. Т. 52. №4. – С. 572.
-
Шагапов В.Ш., Хусаинов И.Г., Дмитриев В.Л. Распространение линейных волн в насыщенных газом пористых средах с учетом межфазного теплообмена. // ПМТФ. 2004. Т.45. № 4. – С. 114-120.
-
Городецкая Н.С.
Волны на границе пористо-упругого полупространства // Акустический вестник. 2005. Т. 8. № 1-2. – С. 28-41. -
Лукин С.В., Губайдуллин А.А., Урманчеев С.Ф. Закономерности отражения волн давления от твердых поверхностей, покрытых пористым слоем // Нефтегазовое дело. 2006. Т.4. №1. – С. 35-40.
-
Губайдуллин А.А., Болдырева О.Ю., Дудко Д.Н. Взаимодействие акустических волн в пористом слое
// Теплофизика и аэродинамика. 2009. Т.16. №3. – С. 455-470. -
Хусаинов И.Г., Дмитриев В.Л. Исследование эволюции волнового импульса при прохождении через пористую преграду // ПМТФ. 2011. Т.52. № 5. – С. 136-145.
-
Володин С.В., Дмитриев В.Л., Хусаинов И.Г. Распространение линейных волн во влажных насыщенных газом пористых средах // ТВТ. 2009. Т. 47. №5. – С. 734-740.
-
Ситдикова Л.Ф., Дмитриев В.Л. Динамика звуковых волн в насыщенных газом пористых средах // Сборник научных трудов II Всероссийской научно-технической конференции с международным участием «Высокие технологии в современной науке и технике». Т.2. – Томск: Изд-во Томского политехнического университета, 2013. – С. 433-438.
-
Гималтдинов И.К., Дмитриев В.Л., Ситдикова Л.Ф. Об эволюции звуковых волн во влажных пористых средах // Фундаментальные исследования. №10 (часть 10), 2013. – С. 2198-2202.
-
Ситдикова Л.Ф., Гималтдинов И.К., Дмитриев В.Л. Учет массо- и теплообмена при распространении акустической волны в пористой среде // Вестник Нижегородского университета им. Н.И. Лобачевского. 2011, №4 (3). – С. 1109-1111.
-
Дмитриев В.Л., Ситдикова Л.Ф. Роль массообмена в акустике влажных пористых сред // Международный сборник научных трудов «Математическое и программное обеспечение систем в промышленной и социальной сферах». Часть 1. Магнитогорск: Изд-во МГТУ им. Г.И. Носова, 2011. – С. 91-95.
-
Дмитриев В.Л. Изучение характеристик насыщенных газом пористых сред на основе отраженного акустического сигнала // Современные научные исследования и инновации. 2014. № 8 [Электронный ресурс]. URL: http://web.snauka.ru/issues/2014/08/36562 (дата обращения: 01.08.2014).
Количество просмотров публикации: Please wait


