Введение
В социальных системах многие переменные являются латентными, т.е. непосредственно не измеряемыми. Такие переменные задаются через набор индикаторов (тестовых заданий), которые можно непосредственно оценить или измерить. Для тестолога и исследователя важно, чтобы тест являлся измерительным инструментом, точно отражал исследуемый латентный параметр. Только качественные измерения могут быть основой для принятия каких-либо решений. Для создания качественного измерителя латентного параметра необходимо грамотно сконструировать систему тестовых заданий [1,2] и подобрать методический инструмент, способный объективно его измерить [3-7]. Изучаемое явление, процесс должны быть описаны с помощью инструмента, позволяющего создавать объективную картину на базе научно-обоснованного подхода. Этим требованиям отвечает современная теория тестирования (модель Раша), признанная в мировом научном сообществе как инструмент для объективного измерения латентных параметров [5-7]. При использовании этого методического инструмента латентная переменная представлена с помощью математической модели. Модель является адекватной, когда корректно, точно отражает действительность. Данная статья рассматривает вопрос точности моделирования латентных переменных с помощью модели Раша.
Выбор и обоснование методических основ для измерения латентных параметров
Модель как образ оцениваемого латентного параметра нуждается в математическом описании на базе известных и хорошо изученных функций. Современная наука в этом контексте рассматривает две теории тестирования: классическую и современную [4]. Классическая теория тестирования (КТТ) была разработана в первой половине 20-го века. Ее основные достоинства заключаются в простоте обработки и интерпретации результатов. Итоговый балл участника тестирования представляет собой дискретную величину и рассчитывается как сумма баллов, полученных за все тестовые задания (ТЗ), возможно, с учетом весовых коэффициентов трудностей этих заданий. При этом следует отметить, что эти баллы способны ранжировать испытуемых только применительно к данному конкретному тесту. Это означает, что если испытуемым будет предложен другой тест (пусть даже в рамках той же учебной дисциплины), то это приведет к другому ранжированию. То же самое справедливо относительно итоговых баллов заданий теста: даже небольшое изменение контингента испытуемых приведет к другим результатам тестирования и соответственно к другим баллам заданий. Этот недостаток КТТ рассматривается как вариативность между уровнем подготовки испытуемых и трудностью теста [3,4]. Также КТТ обладает и другими недостатками [4]: субъективность экспертных весовых коэффициентов, нелинейность шкалы оценивания. Таким образом, КТТ не дает объективных знаний об объекте исследования, тогда как управление требует точной картины состояния изучаемого процесса.
В середине прошлого столетия была решена задача преобразования формальных наблюдений за исходом отдельных случайных событий в измерения, то есть непрерывные переменные со значениями на линейной шкале. Эти преобразования возможны при использовании современной теории тестирования. Мировой опыт измерения и моделирования латентных величин диктует использование модели Раша [3-5]. Ведущая идея модели Раша сводится к обоснованию возможности объективного измерения латентного параметра, эффективного прогнозирования и интерпретации результатов тестирования на фоне широкого диапазона теоретических данных.
Теоретические основы модели Раша
Параметрами модели Раша являются переменные: уровень измеряемой латентной переменной (ИЛП) i-го испытуемого βi и уровень трудности j-го ТЗ dj. Датский ученый Георг Раш трансформировал исходные значения тестовых баллов в шкалу натуральных логарифмов и ввел общую логарифмическую меру для параметров модели βi и dj, названную им логитом (логит – это мера измерения латентной величины в шкале натуральных логарифмов) [3-5]:
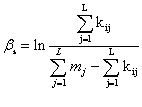 (1),
(1), 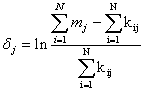 (2), где
(2), где
kij – исходный балл тестирования для i-го испытуемого при выполнении j-го ТЗ, mj – максимально возможный балл, L – количество ТЗ, N – объем выборки. Задачей модели является установка взаимосвязи между двумя множествами βi и dj и распределение их значений на одной линейной шкале логитов (рис. 1).
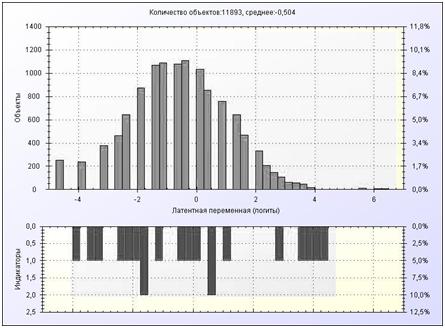
Рис. 1 Распределение ИЛП βi (верхняя гистограмма) и трудностей ТЗ dj (нижняя гистограмма) на одной шкале логитов
Теория латентных переменных имеет вероятностный характер. Она предполагает, что существует одномерный континуум латентной переменной (рис. 2). На этом континууме происходит вероятностное распределение латентной переменной с плотностью Рij. В дихотомической модели Раша это распределение описывается логистической функцией [3-5]:
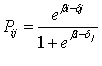 (3),
(3),
Pij – вероятность, что i -й испытуемый выполнит j -е задание; логистическая функция обеспечивает варьирование Pij в интервале [0; 1]. Графически это представлено на рис. 2.
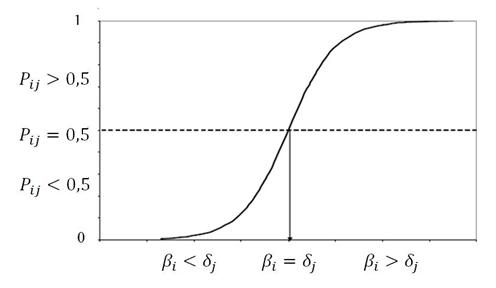
Рис. 2. Вероятность правильного ответа Pij в зависимости от соотношения уровня ИЛП βi и трудности задания dj
Из формулы (3) явно видно, что вероятность успеха испытуемого Pij
зависит от «взаимодействия» двух переменных: уровня подготовленности βi и трудности задания dj. Логично сделать вывод, что если уровень подготовленности i-го испытуемого превышает трудность j-го задания, то испытуемый, скорее всего, ответит правильно на это задание. И наоборот, если уровень способности i-го испытуемого меньше трудности j-го задания, то испытуемый, скорее всего, не ответит на это задание.
Заметим, что распределение значений вычисленных параметров (формулы 1,2) на незначительной выборке не дает целостной картины изучаемого процесса, а погрешности реальных измерений не позволяют описать процесс с помощью известной математической функции. Для нахождения устойчивых оценок латентных параметров обычно используется итерационная процедура с помощью метода максимального правдоподобия Р.Фишера [4]. Задача итерационной процедуры заключается в нахождении таких оценок параметров и , которые при подстановке в логистическую функцию (3) давали бы значения вероятности , близкие к ответу i-го испытуемого на j-е задание теста. Например, если i-й испытуемый за j-е задание получил 0 баллов, то вероятность должна быть близка к 0.
Ограничения практического применения модели Раша, логические основания модели
Обращаем внимание на то, что, не смотря на все достоинства модели Раша, не всякое содержание может быть описано с ее помощью. Первичным при использовании модели является ответ на вопрос: «Является ли конструкт пригодным для описания рассматриваемого латентного парметра с помощью теории Раша?». Рассмотрим условия для построения качественного измерителя.
-
Одномерность конструкта
Модель Раша предполагает, что оцениваемый латентный параметр одномерный (тест измеряет только одну латентную величину), а сам тест гомогенный.
-
Наличие четко выраженного свойства измеряемого параметра
Модель Раша предполагает вероятностную зависимость активности объекта (испытуемого) по каждому конкретному индикатору от уровня ИЛП в целом, т.е., чем более выражено у объекта измеряемое латентное качество вцелом, тем в большей степени оно должно быть выражено по всем индикаторам. Основной постулат модели: испытуемый с более выраженной ИЛП проявляет бОльшую активность по всем индикаторам, чем испытуемый с менее выраженной ИЛП. Выполнение этого условия свидетельствует о пригодности того или иного индикатора и его соответствии логическому основанию модели.
Следует отметить, что существуют некоторые условия, не относящиеся к логическому основанию модели, но нарушающие правильный профиль результатов тестирования и, таким образом, негативно влияющие на качество (точность) измерения. К таким условиям относятся:
-
необъективное оценивание со стороны экспертов, их некомпетентность,
-
низкое качество конструирования ТЗ и теста вцелом,
-
нарушение регламента тестирования (списывание, подсказывание, неблагоприятные условия тестирования).
Согласованность экспериментальных и модельных данных
Для признания теоретических значений параметров модели в качестве «истинных», необходимо оценить соответствие экспериментальных данных модели. Обоснование вывода о качестве теста, а следовательно, и о пригодности предлагаемой системы ТЗ для измерения уровня подготовленности испытуемых нуждается в эмпирических фактах. Показателем совместимости теоретических и экспериментальных данных является критерий согласия хи-квадрат, количественное значение вероятности которого не менее 0,05 [3,4]. Рассмотрим этот вопрос на примере построения модели уровня подготовки выпускников средней школы по математике города Омска и Омской области [8].
Совместимости набора ТЗ
Одним из логических оснований модели является одномерность (гомогенность) конструкта, все ТЗ должны измерять одну и ту же латентную величину. Совместимость набора индикаторных переменных и одновременно степень соответствия данных тестирования модели измерения оценивается с помощью эмпирического уровня значимости хи-квадрат. В нашем случае критерий согласия хи-квадрат больше 0,05 и соответствует значению 1 (рис. 3). Вне сомнения, этот показатель считается более чем удовлетворительным и свидетельствует о высокой точности моделирования. Это означает, что полученные результаты тестирования с помощью представленного в тесте набора ТЗ можно использовать как для измерения рассматриваемой латентной переменной, так и для измерения уровня трудности ТЗ [9].

Рис. 3 Суммарные статистики теста ЕГЭ по математике
Соответствие ТЗ модели измерения
Необходимость рассмотрения соответствия ТЗ модели измерения объясняется тем, что в целом результаты тестирования могут соответствовать модели измерения (п. 5.1.), однако даже в таком наборе могут оказаться задания, не соответствующие модели или не достаточно эффективные с точки зрения точности моделирования. Поэтому представляется целесообразным рассмотреть ТЗ более подробно. «Работу» каждого ТЗ наглядно демонстрирует его характеристическая кривая (рис.2,4). На характеристических кривых ТЗ по оси абсцисс отложена ИЛП в логитах, по оси ординат – вероятность правильного ответа. Континуум (непрерывная кривая) показывает модельные значения, а точки – средние экспериментальные значения групп испытуемых.
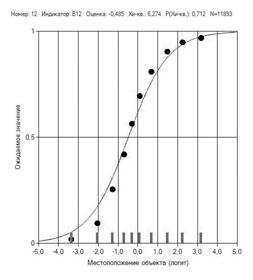
Рис. 4 Характеристическая кривая ТЗ
Степень совместимости каждой индикаторной переменной со всем набором индикаторных переменных, т.е. соответствие индикаторных переменных модели определяется на основе критерия Хи-квадрат следующим образом. Измеряемые объекты по полученным экспериментальным оценкам делятся на примерно равные группы. Количество групп определяется объемом выборки, в нашем случае их 10. Далее для каждой группы вычисляется среднее значение ИЛП (точки на рис. 4) и на основе критерия Хи-квадрат определяется соответствие значений экспериментальных точек теоретическим значениям (непрерывная кривая на рис. 2). Если уровень значимости статистики Хи-квадрат для индикаторной переменной меньше 0,05, то соответствующая индикаторная переменная плохо совместима с остальными и является кандидатом на исключение. В табл. 1 представлены статистические характеристики ТЗ.
Таблица 1. Статистические характеристики тестовых заданий
|
ТЗ |
Оценка, логит |
Ст. ошибка |
P(Хи-квадрат) |
|
В1 |
-3,11996 |
0,030767125 |
0,369701775 |
|
В2 |
-3,92255 |
0,037979988 |
0,717879993 |
|
В3 |
-3,25873 |
0,031812288 |
0,957233875 |
|
В4 |
-1,5712 |
0,023604301 |
0,115761346 |
|
В5 |
-2,37934 |
0,02639562 |
0,983072778 |
|
В6 |
-1,75773 |
0,024086853 |
0,997914589 |
|
В7 |
-1,22489 |
0,022942206 |
0,886216513 |
|
В8 |
-0,24214 |
0,022563223 |
0,922865611 |
|
В9 |
-1,50733 |
0,023459775 |
0,162232155 |
|
В10 |
-2,04656 |
0,025019979 |
0,961977307 |
|
В11 |
0,690891 |
0,024121626 |
0,988095186 |
|
В12 |
-0,48511 |
0,022461482 |
0,712225498 |
|
В13 |
0,039725 |
0,022837333 |
0,938427021 |
|
В14 |
0,528816 |
0,023714792 |
0,984443429 |
|
С1 |
1,117992 |
0,01759495 |
0,605240685 |
|
С2 |
3,72772 |
0,045445929 |
0,999943033 |
|
С3 |
2,813047 |
0,023723527 |
0,923542405 |
|
С4 |
3,947788 |
0,030999459 |
0,996329923 |
|
С5 |
4,170184 |
0,048922503 |
0,999301877 |
|
С6 |
4,479386 |
0,04190918 |
0,974967612 |
Из тал. 1 видно, что все ТЗ имеют приемлемые показатели качества. ТЗ В4 имеет наименьший показатель вероятности хи-квадрат, равный 0,116, что, тем не менее, выше критериального значения 0,05. Таким образом, все ТЗ и тест в целом соответствуют модели, ее логическому основанию. Это свидетельствует о пригодности данных для измерения и дает основание исследовать качество теста с помощью модели Раша [8-10].
Заметим, что несоответствие ТЗ модели измерения связано с композицией (форма, содержание) ТЗ, т.к. качество теста корнями уходит в содержание конструкта [1,2]. Рассмотрим некоторые требования к ТЗ к 1-2 уровню познавательной деятельности по Лернеру [1,2]:
-
ТЗ должно быть ясным и понятным по смыслу, легко и быстро восприниматься. Содержание ТЗ не должно содержать повторов, двойных отрицаний и сленга. По возможности, текст ТЗ не должен содержать сложноподчиненные конструкции, по конструкции он должен быть простым. ТЗ должно быть технологично построено, желательна схематичность, свернутость вопроса, использование рисунков, схем и других поясняющих объектов.
- ТЗ должно быть однозначным, конкретным, направленным на один исследуемый признак. По возможности специфический признак, ключевое слово выносится в начало ТЗ. Ответы на ТЗ также должны быть однозначными, не допускается применение обобщающих слов: всегда, никогда, иногда, все…
-
ТЗ должно быть содержательно валидно, значимо для данной предметной области, тест вцелом должен целостно и системно охватывать материал.
-
ТЗ должны быть различны по трудности, сложности, охватывать различные уровни познавательной деятельности.
-
В формулировке ТЗ не должно быть подсказок. В заданиях закрытого типа не должно быть ответов, содержащих явно выделяющихся, обособленных ответов. Дистракторы должны быть близки по смыслу и равновероятны, равнопривлекательны для незнающих правильного ответа.
-
Запрещено применение всех правильных ответов или всех неправильных. Недопустимы ответы типа: «все выше перечисленное верно», «все указанные ответы – неверны» и т.п.
-
Когда ответы к закрытым заданиям указывают на устойчивое нарастание или снижение какого-либо качества или свойства, то их лучше упорядочить.
-
Все ответы должны быть параллельными по конструкции (стиль, длина) и грамматически согласованными с основной частью задания теста.
Библиографический список
- Челышкова М.Б. Теория и практика конструирования педагогических тестов: Учебное пособие. – М.: Логос, 2002. – 432 с.
-
Аванесов B.C. «Композиция тестовых заданий». Учебная книга. 3 изд.. доп. М.: Центр тестирования, 2002г. -240 с.
-
Нейман Ю.М., Хлебников В.А. Педагогическое тестирование как измерение. Учебное пособие, ч.1. – М.: Центр Тестирования МО РФ. – 2002. – 67 с.
-
Маслак, А.А. Измерение латентных переменных в социальных системах / А.А. Маслак. – Славянск-на-Кубани: Издательский центр СГПИ. 2012. -432 с.
-
Masters N. G. The Key to Objective Measurement. Australian Council on Educational Research, 2001.
-
Летова Л.В. Объективные измерения и моделирование латентных величин в образовании // Образование и наука. 2013. №8. – С. 75-88.
-
Летова Л.В. Объективность измерений латентных переменных // Дистанционное и виртуальное обучение. 2014. №3. – С. 83-94.
-
Летова Л.В. Исследование качества теста единого государственного экзамена по математике с помощью модели Раша
// Управление образованием: теория и практика. 2013. №1(9). – С. 89-99. -
Летова Л.В. Исследование качества теста как измерительного инструмента // Дистанционное и виртуальное обучение. 2013. №11. – С. 116 – 125.
-
Летова Л.В. Точность измерения латентных переменных // Дистанционное и виртуальное обучение. 2013. №12. – С. 75-88.
-
Летова Л.В. Исследование влияния неравномерного распределения тестовых заданий на точность измерения латентных параметров (часть 1) // Современные научные исследования и инновации. – Апрель 2014. – № 4 [Электронный ресурс]. URL: http://web.snauka.ru/issues/2014/04/33733 (дата обращения: 21.04.2014).
-
Летова Л.В. Исследование влияния неравномерного распределения тестовых заданий на точность измерения латентных параметров (часть 2) // Современные научные исследования и инновации. – Май 2014. – № 5 [Электронный ресурс]. URL: http://web.snauka.ru/issues/2014/05/33827
Количество просмотров публикации: Please wait


