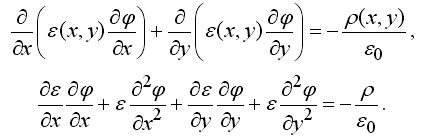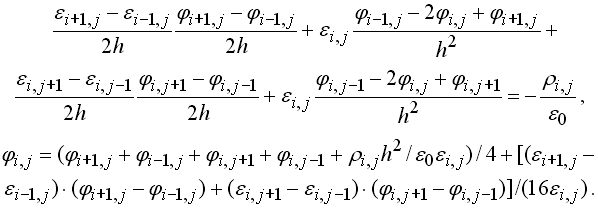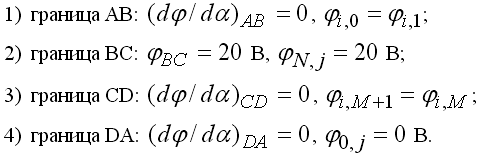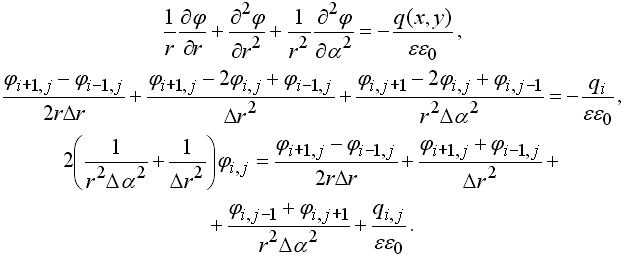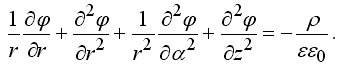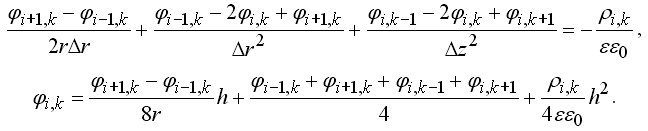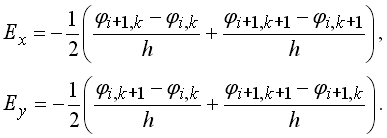При изучении основ компьютерного моделирования имеет смысл рассмотреть вопрос о численном решении уравнения Пуассона при расчете электростатического поля в однородный и неоднородных средах в различных системах координат [1-8]. Допустим, известны плотность распределения заряда и потенциал на границе области двумерной неоднородной среды. В декартовых координатах распределение потенциала удовлетворяет уравнению:
Чтобы решить это уравнение на ЭВМ, запишем его в конечных разностях. Для этого заменим производные их конечно-разностными аппроксимациями:
Для решения рассматриваемой стационарной задачи используется релаксационный метод последовательных приближений: во всех внутренних узлах сетки задаются произвольные исходные значения потенциала; его значения во внешних узлах должны соответствовать граничным условиям. Осуществляется первая итерация, в ходе которой перебираются все внутренние узлы сетки и, исходя из начальных значений, определяют новые уточненные значения функции. Затем осуществляются второе, третье, … приближения, причем результаты i–ой итерации используются в качестве исходных для (i+1)-ой итерации. В результате получающиеся значения приближаются к истинному распределению потенциала.
Для реализации этого алгоритма требуется зарезервировать в памяти ЭВМ три двумерных массива размерностью N x M, элементами которых являются числа типа real или single (язык Pascal). Один массив для диэлектрической проницаемости, два других –– для потенциалов на шаге t и t+1. Это не позволяет в среде Free Pascal создать сетку с большим числом узлов. Увеличить число узлов можно, задав диэлектрическую проницаемость целыми числами. Вместо двух массивов для потенциалов на различных временных слоях следует создать один, но в этом случае, чтобы избежать накапливания ошибок, придется перебирать элементы в четырех различных направлениях.
Алгоритм состоит в последовательном переборе узлов сетки слева на право и справа на лево, сверху вниз и снизу вверх, в ходе которого вычисляются значения потенциала в них. Перед каждым проходом следует учесть граничные условия задачи, то есть приравнять потенциалы на границе двумерной области к заданной величине или функции координат. Используемая программа ПР–1 содержит: 1) процедуру Sreda, в которой задается диэлектрическая проницаемость среды в узлах сетки; 2) процедуру Gran, в которой учитывается распределение потенциала вдоль границы области; 3) процедуру Raschet, в которой задается распределение заряда и вычисляется потенциал в различных узлах (i, j); 4) процедуру Draw, выводящую результат вычислений на экран; 5) основную часть программы, в которой осуществляется вызов перечисленных процедур в требуемом порядке [3-5].
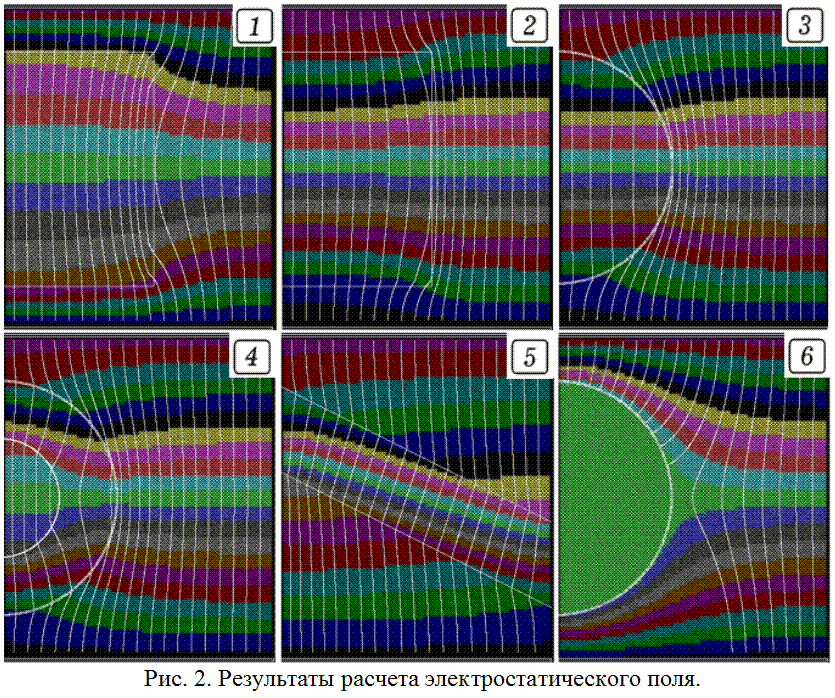
На рис. 1.1 и 2 представлены результаты ее использования для расчета электрического поля в двумерной неоднородной среде с диэлектрической проницаемостью eps = 1+a*x*y, созданным двумя пластинами, которые имеют потенциалы 350 и –350 В, и зарядами q1 и q2. В пространстве между пластинами имеется заземленный проводник, его потенциал равен нулю.
Задавая различные распределения зарядов, потенциалов, диэлектрической проницаемости среды и граничные условия, можно решить и другие задачи. Например, рассчитать электрическое поле, создаваемое двумя параллельными разноименно заряженными пластинами, в случаях, когда в пространство между ними внесен: 1) прямоугольный брусок с диэлектрической проницаемостью меньшей, чем у окружающей среды (рис. 2.1); 2) прямоугольный брусок с диэлектрической проницаемостью большей, чем у окружающей среды (рис. 2.2); 3) цилиндр с диэлектрической проницаемостью большей, чем у окружающей среды (рис. 2.3); 4) труба с с диэлектрической проницаемостью большей, чем у окружающей среды (рис. 2.4); 5) пластина с диэлектрической проницаемостью большей, чем у окружающей среды, расположенная под углом (рис. 2.5); 6) металлический цилиндр (рис. 2.6). Программа ПР–2 рассчитывает линии равного потенциала и силовые линии электрического поля в случае, когда в пространство между заряженными пластинами внесена труба с диэлектрической проницаемостью большей, чем у окружающей среды. Из рисунков видно, что на границе раздела различных сред происходит преломление силовых линий; причем в средах с большей диэлектрической проницаемостью они располагаются реже (напряженность меньше). При внесении в электрическое поле проводящего цилиндра (потенциалы всех его точек равны), силовые линии оказываются перпендикулярными к поверхности.
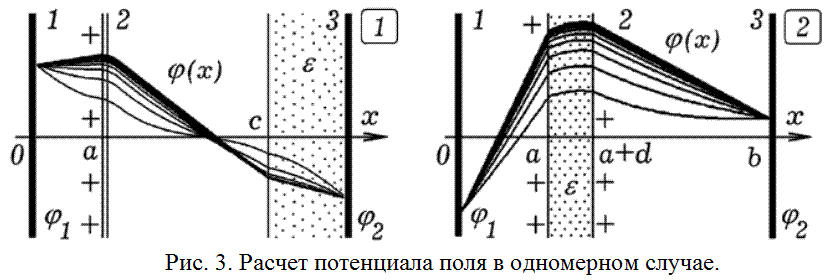
Рассмотренный выше подход позволяет решить одномерную задачу, например, рассчитать распределение потенциала электростатического поля между двумя бесконечно большими пластинами 1 и 3, расположенными перпендикулярно оси Ox на расстоянии b друг от друга (рис. 3.1). Потенциалы пластин заданы; между ними расположена пластина 2 из диэлектрика, заряженная положительно или отрицательно. Рядом с пластиной 3 имеется слой диэлектрика с некоторой диэлектрической проницаемостью. На рис. 3.2 показано получающееся распределение потенциала вдоль оси Ox в случае, когда между металлическими пластинами имеется толстая пластина с заданной диэлектрической проницаемостью, внутри которой равномерно “размазан” электрический заряд. Представлено не только искомое распределение потенциала, но и несколько предшествующих ему приближений; это помогает понять сущность метода последовательных итераций [3-5].
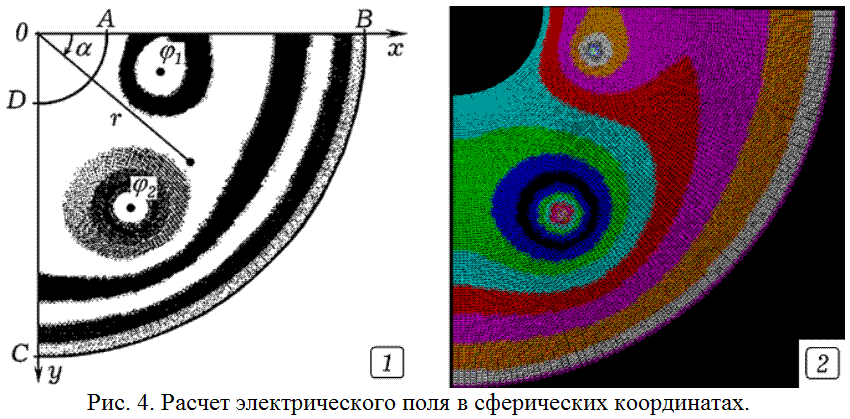
Выше рассмотрены методы решения уравнения Пуассона в декартовых координатах. Теперь рассчитаем распределение потенциала в двумерной области, имеющей форму четверти круга, для чего решим уравнение Пуассона в полярных координатах (рис. 4.1). Граничные условия зададим так:
Потенциалы двух точек поддерживаются равными 50 В и – 80 В. Уравнение Пуассона в полярных координатах и соответствующее конечно-разностное уравнение имеют вид:
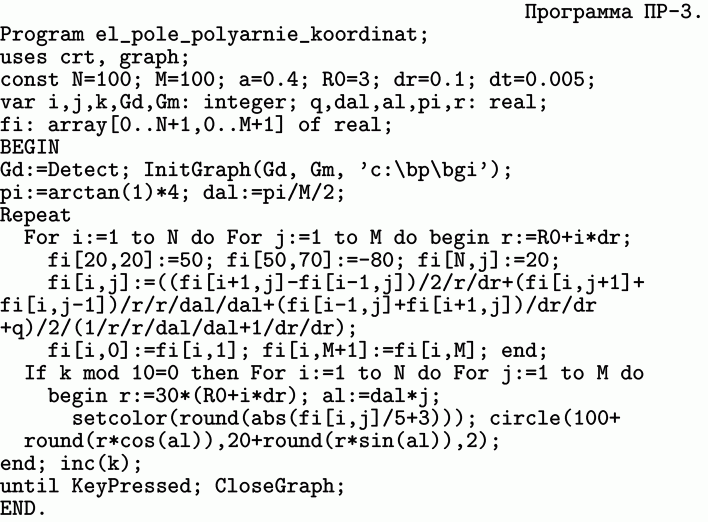
Отсюда выражают потенциал в узле (i, j). Для решения задачи используется программа ПР-3. Результаты вычисления распределения потенциала в двумерной области при заданных граничных условиях представлены на рис. 4.2. Программа выполняет последовательность итераций, получающиеся значения потенциалов постепенно приближаются к искомым значениям, которые соответствуют точному решению задачи.
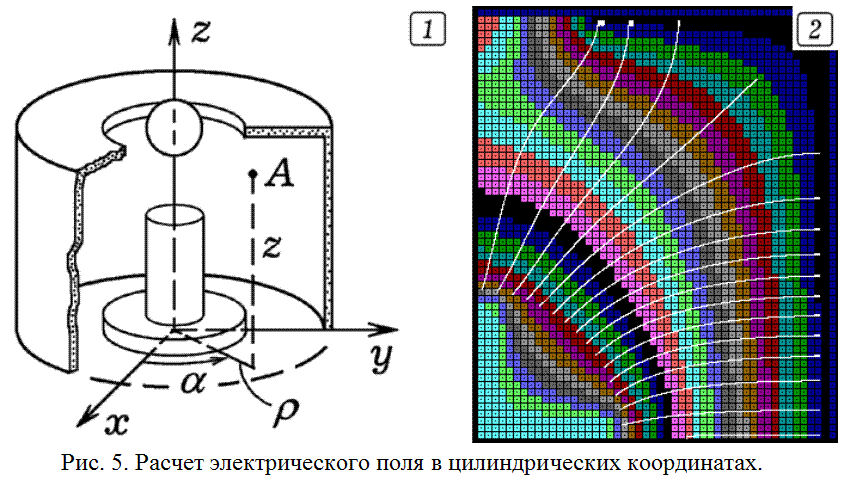
Теперь рассчитаем электростатическое поле в пространстве между двумя электродами 1 и 2 при наличии заряженного шара 3 (рис. 5.1), используя цилиндрические координаты. Распределение потенциала должно удовлетворять уравнению Пуассона:
Электроды обладают цилиндрической симметрией, то же самое относится к распределению заряда и граничным условиям. Задача сводится к нахождению распределения потенциала в плоскости осевого сечения xOz. В конечных разностях получаем:
Используется программа ПР-4, в которой перебираются все узлы двумерной сетки и с каждой итерацией пересчитываются значения потенциала. После 5000 итераций осуществляется построение силовых линий. Для этого в пространство между электродами запускаются невесомые частицы–маркеры, которые перемещаются вдоль силовых линий и рисуют свою траекторию. Напряженность поля равна градиенту потенциала.Для определения направления силовой линии в точке с координатами x, z используются формулы:
Результаты расчета электростатического поля представлены на рис. 5.2. Силовые линии перпендикулярны эквипотенциальным поверхностям и направлены от положительного электрода к отрицательному.
Обсуждение и анализ рассмотренных выше задач на занятиях по компьютерному моделированию способствуют более глубокому пониманию методов решения дифференциальных уравнений с частными производными, повышает интерес студентов к программированию, физике и математике.
Библиографический список
- Гулд Х., Тобочник Я. Компьютерное моделирование в физике: В 2-х частях. Часть 1. –– М.: Мир, 1990. –– 349 с.
- Кунин С. Вычислительная физика. –– М.: Мир, 1992. –– 518 с.
- Майер Р.В. Задачи, алгоритмы, программы. [Электронный ресурс] / URL: http://maier-rv.glazov.net, http://komp-model.narod.ru.
- Майер Р.В. Компьютерное моделирование: Глава 12. Расчет электрического и магнитного полей. Движение заряженных частиц [Электронный ресурс] / URL: http://maier-rv.glazov.net, http://mayer.hop.ru.
- Майер Р.В. Компьютерное моделирование физических явлений. –– Глазов, ГГПИ: 2009. –– 112 с.
- Giordano N.J. Computational Physics. –– New Jersey, Prentice Hall, 1997. – 419 p.
- Phillipson P.E., Schuster P. Modeling by Nonlinear Differential Equations: Dissipative and Conservative Processes. –– World Scientific Publishing, 2009. –– 225 p.
- Woolfson M.M., Pert G.J. An Introduction to Computer Simulation. –– Oxford University Press, 1999. –– 311 p.
Количество просмотров публикации: Please wait