В настоящее время в математической теории существует много подходов к решению задач исследования и моделирования сложных систем. Как правило, задачи исследования и моделирования не формулируются ясно, а приводятся часто в столь неопределенных терминах, что их математическая трактовка априори зачастую невозможна, так как неясно даже о достижении какой цели идет речь. Применение точных методов не возможно там, где нет ясности ни в концепциях, ни в задачах, к которым эти методы должны прилагаться [1].
Как правило, невозможно четко описать состояние системы, представить параметры, описывающие систему, в виде четких, определенных чисел. Причин может быть несколько: воздействие на систему внешней среды (экономические, политические, человеческие, экологические и прочие факторы); внутренние изменения сложной неравновесной системы (нехватка и выход из строя оборудования, трудовых ресурсов, транспортировка продукции и.т.п.); динамичное изменение планов производства в системе и многое другое. В связи с этим целесообразно представить исследуемые параметры неравновесной системы в виде нечетких оценок.
В условиях полной дефицитности реальный нечеткий выбор понимается как своеобразное «пожелание» элемента потребления. Модель нечеткого спроса будем создавать при условии представления о потребительском нечетком спросе, как о желаемом для элемента потребления количестве данного изделия (продукта), в общем случае нечеткого, в сложившейся ситуации «производства – потребления».
Пусть известно, что желаемое для элемента потребления нечеткое количество изделия (продукта) i равно Fi, 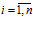 , а вектор ограничений-квот на каждый продукт X**=(
, а вектор ограничений-квот на каждый продукт X**=(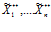 ). Тогда реально взятое элементом потребления нечеткое количество изделия (продукта) i
). Тогда реально взятое элементом потребления нечеткое количество изделия (продукта) i 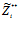 равно множеству желаемого для элемента потребления нечеткого количества i-го изделия (продукта) Fi, при условии, что Fi нечетко не больше ограничения-квоты на i-е изделие (продукт); либо равно ограничению-квоте на i-е изделие (продукт), при условии, что Fi нечетко больше величины ограничения-квоты на всех наборах индекса iÎW={1,2,…,n} [2,3]:
равно множеству желаемого для элемента потребления нечеткого количества i-го изделия (продукта) Fi, при условии, что Fi нечетко не больше ограничения-квоты на i-е изделие (продукт); либо равно ограничению-квоте на i-е изделие (продукт), при условии, что Fi нечетко больше величины ограничения-квоты на всех наборах индекса iÎW={1,2,…,n} [2,3]:
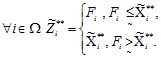 (1)
(1)
Из формулы (1) следует, что элемент потребления приобретет i-ое изделие (продукт) целиком, если его желания Fi существующее ограничение-квоту нечетко превышают, iÎW.
Желаемое количество Fi может произвольно зависеть от величин ограничений-квот на все продукты, т.е. Fi=Fi(Х**), 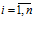 и F(Х**)={F1(Х**),…,Fn(Х**)} есть заданная векторная функция нечеткого спроса. Тогда правило (1) определяет реальный нечеткий выбор, порождаемый заданным нечетким спросом.
и F(Х**)={F1(Х**),…,Fn(Х**)} есть заданная векторная функция нечеткого спроса. Тогда правило (1) определяет реальный нечеткий выбор, порождаемый заданным нечетким спросом.
Если известна функция F(Х**) потребительского нечеткого спроса, то нечеткие компоненты fi(X**), 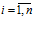 функции f(X**) потребительского нечеткого выбора будут определены функцией потребительского нечеткого спроса следующим образом. Нечеткая компонента функции выбора элемента потребления будет равна минимальному значению из множества нечетких ограничений-квот на i-е изделия (продукты) и желаемого нечеткого количества i-го изделия (продукта). Функция выбора элемента потребления будет равна минимуму среди множества ограничений-квот, наложенных на выбираемые элементом потребления изделия (продукты) и множества желаемого количества изделий (продуктов) для элемента потребления:
функции f(X**) потребительского нечеткого выбора будут определены функцией потребительского нечеткого спроса следующим образом. Нечеткая компонента функции выбора элемента потребления будет равна минимальному значению из множества нечетких ограничений-квот на i-е изделия (продукты) и желаемого нечеткого количества i-го изделия (продукта). Функция выбора элемента потребления будет равна минимуму среди множества ограничений-квот, наложенных на выбираемые элементом потребления изделия (продукты) и множества желаемого количества изделий (продуктов) для элемента потребления:
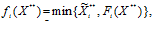 iÎW (2)
iÎW (2)
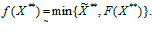 (3)
(3)
Функция f(X**) удовлетворяет требованию неотрицательности и ограниченности 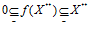 . Для любой функции нечеткого выбора f(X**) можно найти порождающую функцию F(Х**) нечеткого спроса. В крайнем случае, в качестве порождающей функции F(Х**) нечеткого спроса может быть взята сама функция f(X**) нечеткого потребительского выбора.
. Для любой функции нечеткого выбора f(X**) можно найти порождающую функцию F(Х**) нечеткого спроса. В крайнем случае, в качестве порождающей функции F(Х**) нечеткого спроса может быть взята сама функция f(X**) нечеткого потребительского выбора.
Векторная функция F(Х**) потребительского нечеткого спроса будет нечетко субрегулярна, если каждая ее нечеткая компонента Fi(Х**), 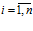 , рассматриваемая как функция от нечеткой величины
, рассматриваемая как функция от нечеткой величины 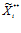 ,
, 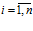 , при произвольных фиксированных
, при произвольных фиксированных 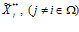 , удовлетворяет условию:
, удовлетворяет условию:
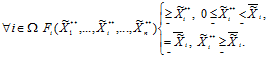 (4)
(4)
т.е. каждая нечеткая компонента Fi(Х**), 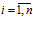 функции F(Х**) нечетко больше либо равна значению ограничения-квоты i-го изделия (продукта), при условии, что квота на i-ое изделие (продукт) нечетко неотрицательна и ограничена сверху, или равна некоторой нечеткой величине
функции F(Х**) нечетко больше либо равна значению ограничения-квоты i-го изделия (продукта), при условии, что квота на i-ое изделие (продукт) нечетко неотрицательна и ограничена сверху, или равна некоторой нечеткой величине 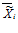 , при условии, что эта нечеткая величина нечетко не больше значения i-ой ограничения-квоты.
, при условии, что эта нечеткая величина нечетко не больше значения i-ой ограничения-квоты.
Величина Fj(Х**), определяющая нечеткий выбор j-го изделия (продукта) (j¹iÎW) должна быть определена для другого нечеткого состояния, в котором остается нечетко постоянным ограничение 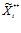 , а уменьшается нечеткое ограничение
, а уменьшается нечеткое ограничение 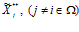 . Это и вызывает несогласованность и несовместимость в решениях для векторной функции F(Х**) потребительского нечеткого выбора в целом [2,3].
. Это и вызывает несогласованность и несовместимость в решениях для векторной функции F(Х**) потребительского нечеткого выбора в целом [2,3].
Сформулируем аналог свойства независимости нечеткого выбора для векторной функции F(Х**) потребительского нечеткого спроса.
Если для векторов X**=(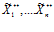 ), Y**=(
), Y**=(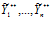 ) выполняются следующие условия:
) выполняются следующие условия:
- для любых iÎW при нечетком включении ограничении-квоты на изделие (продукт) i в функцию спроса на i-ое изделие (продукт), нечеткое ограничение-квоты на i-ое изделие нечетко равна выпускаемому количеству i-го изделия;
- для любых iÎW при нечетком включении функции спроса на i-ое изделие (продукт) в ограничение-квоту на изделие (продукт) i, то нечеткое ограничение-квоты на i-ое изделие нечетко включается в выпускаемое количество i-го изделия (продукта) и нечетко включается в функцию спроса на i-ое изделие (продукт):
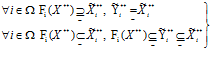 , (5)
, (5)
то:- для любых iÎW при нечетком включении ограничении-квоты на изделие (продукт) i в функцию спроса на i-ое изделие (продукт), выпускаемое количество i-ого изделия (продукта) нечетко включается в функцию спроса на выпускаемую продукцию;
- для любых iÎW при нечетком включении функции спроса на i-ое изделие (продукт) в ограничение-квоту на изделие (продукт) i, то функция спроса элемента потребления нечетко равна функции спроса на выпускаемую продукцию и нечетко включается в множество выпускаемой продукции, либо функция спроса элемента потребления нечетко равна функции спроса на выпускаемую продукцию и нечетко не включается в множество выпускаемой продукции:
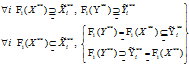 . (6)
. (6)
Выражениями (5) и (6) определяется свойство сужения допустимых альтернатив потребительского нечеткого спроса.
Если для векторов X**=(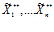 ), Y=(
), Y=(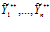 ) при любых наборах iÎW при нечетком включении ограничении-квоты на изделие (продукт) i в функцию спроса на i-ое изделие (продукт), нечеткое ограничение-квоты на i-е изделие нечетко равна выпускаемому количеству i-го изделия; либо на любых наборах iÎW при нечетком включении функции спроса на i-ое изделие (продукт) в ограничение-квоту на изделие (продукт) i, то нечеткое ограничение-квоты на i-е изделие (продукт) нечетко не включается в выпускаемое количество i-го изделия (продукта):
) при любых наборах iÎW при нечетком включении ограничении-квоты на изделие (продукт) i в функцию спроса на i-ое изделие (продукт), нечеткое ограничение-квоты на i-е изделие нечетко равна выпускаемому количеству i-го изделия; либо на любых наборах iÎW при нечетком включении функции спроса на i-ое изделие (продукт) в ограничение-квоту на изделие (продукт) i, то нечеткое ограничение-квоты на i-е изделие (продукт) нечетко не включается в выпускаемое количество i-го изделия (продукта):
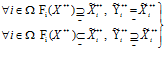 , (7)
, (7)
то при любых наборах iÎW при нечетком включении ограничении-квоты на изделие (продукт) i в функцию спроса на i-ое изделие (продукт), нечеткое количество выпускаемой продукции также нечетко включается в функцию спроса выпускаемой продукции i; либо при нечетком включении функции спроса на i-ое изделие (продукт) в ограничение-квоту на изделие (продукт) i, функция спроса элемента потребления нечетко равна функции спроса на выпускаемую продукцию и нечетко включается в множество выпускаемого i-го изделия (продукта):
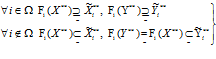 . (8)
. (8)
Аналогом свойства (5) потребительского нечеткого выбора является следующее свойство для потребительского нечеткого спроса.
Если для векторов X**=(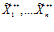 ), Y**=(
), Y**=(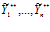 ) справедливо то, что при любых наборах iÎW при нечетком включении ограничении-квоты на изделие (продукт) i в функцию спроса на i-ое изделие (продукт), нечеткая ограничение-квота на i-ое изделие нечетко равна выпускаемому количеству i-го изделия; либо при нечетком включении функции спроса на i-ое изделие (продукт) в ограничение-квоту на изделие (продукт) i, нечеткая функция потребительского спроса на i-ое изделие (продукт) нечетко включается в выпускаемое количество i-го изделия (продукта):
) справедливо то, что при любых наборах iÎW при нечетком включении ограничении-квоты на изделие (продукт) i в функцию спроса на i-ое изделие (продукт), нечеткая ограничение-квота на i-ое изделие нечетко равна выпускаемому количеству i-го изделия; либо при нечетком включении функции спроса на i-ое изделие (продукт) в ограничение-квоту на изделие (продукт) i, нечеткая функция потребительского спроса на i-ое изделие (продукт) нечетко включается в выпускаемое количество i-го изделия (продукта):
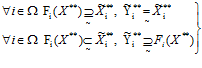 , (9)
, (9)
то на любых наборах iÎW при нечетком включении ограничении-квоты на изделие (продукт) i в функцию спроса на i-е изделие (продукт), выпускаемое количество i-ого изделия (продукта) нечетко включается в функцию спроса на выпускаемую продукцию; либо на любых наборах iÎW при нечетком включении функции спроса на i-ое изделие (продукт) в ограничение-квоту на изделие (продукт) i, функция спроса элемента потребления нечетко равна функции спроса на выпускаемую продукцию и нечетко включается в множество выпускаемой продукции, либо функция спроса элемента потребления нечетко равна функции спроса на выпускаемую продукцию и нечетко не включается в множество выпускаемой продукции:
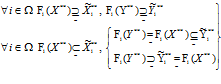 . (10)
. (10)
И последнее, что следует отметить для векторной функции F(X**) потребительского нечеткого спроса.
Векторная функция потребительского нечеткого спроса является нечетко нормальной и порождает нечетко нормальную функцию f(X**) нечеткого выбора, если векторная функция F(X**) непрерывна и ограничена, т.е. существует некоторая константа P, которая для любых i из W ограничивает функцию нечеткого потребительского спроса на i-ое изделие (продукт):
“iÎW Fi<P, (11)
где Р – некоторая константа.
Так как затраты на производство, выпуски изделий (продуктов) для реализации, ограничения–квоты носят нечеткий характер, то при описании поведения элемента потребления путем задания функций выбора следует ввести понятия нечеткого выбора, нечеткой функции выбора [4].
Введение нечетких понятий при определении выбора элемента потребления позволит:
- указать наиболее возможный диапазон изменения параметров поведения элемента потребления;
- учитывать не только бюджетные ограничения элемента потребления, но и реальные, нечетко заданные ограничения-квоты на потребление дефицитных изделий (продуктов).
Библиографический список
- Федосеев В. В. Математическое моделирование в экономике и социологии труда: методы, модели, задачи: учебное пособие для студентов высших учебных заведений. – М. : ЮНИТИ-ДАНА, 2007.
- Заргарян Е.В. Модель нечеткого производственного баланса. Сб. тезисов докладов международной научной конференции «Проблемы развития естественных, технических и социальных систем». Ч.1 – Таганрог: Изд-во «Антон», ТТИ ЮФУ, 2007.
- Заргарян Е.В. Методы нечеткого интервального анализа. Труды Всероссийской научной конференции «Актуальные вопросы исследования общественных и технических систем», Часть 2. – Таганрог: Изд-во ТТИ ЮФУ, 2011. С. 30-31.
- Заргарян Ю.А. Ситуационные модели принятия решений в задачах менеджмента. Труды Ежегодной научной конференции студентов и аспирантов базовых кафедр ЮНЦ РАН. – Ростов н/Д: Изд-во ЮНЦ РАН, 2009.
Количество просмотров публикации: Please wait


