Курс “Компьютерное моделирование” предполагает изучение основных методов моделирования физических систем. Это относится и к методу больших частиц, который является развитием метода молекулярной динамики. Он состоит в замене тела совокупностью крупных шарообразных частиц, взаимодействующих и движущихся в соответствии с законами классической механики [1–5]. При удалении частицы притягиваются, а при сближении отталкиваются. Движение каждой частицы, ее координаты и скорость могут быть рассчитаны из второго закона Ньютона. Все это позволяет определить состояние системы в последующие моменты времени. Методика изучения метода больших частиц может быть сведена к решению следующих задач.
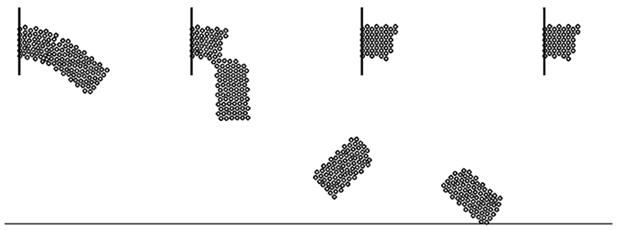
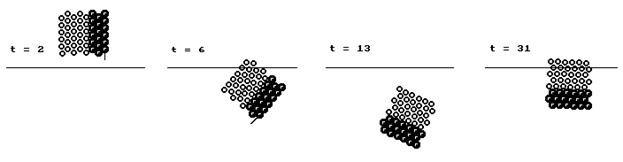
Задача 1. Вязкоупругий стержень, двигаясь по инерции в поле тяжести, соударяется с горизонтальной поверхностью, деформируется, отскакивает от нее, переворачивается и снова падает на поверхность. Необходимо промоделировать это явление.
Вместо стержня рассмотрим совокупность твердых макроскопических частиц (шариков или дисков), взаимодействующих друг с другом с заданными силами притяжения, отталкивания и внутреннего трения. Расстояние между центрами частиц обозначим через r. Проекцию F_r силы взаимодействия на ось r зададим так: 1) если r > 10, то частицы не взаимодействуют: F_r = 0; 2) если r лежит в интервале [6; 10], то между частицами действует сила упругости F_r=1000(8–r); 3) если r < 6, то частицы отталкиваются: F_r = 10000. Величины r и F_r заданы в условных единицах.
При неупругих деформациях тела, когда i–тая частица смещается относительно соседней j–той частицы, на i–тую частицу действует сила вязкого трения. Она направлена в сторону противоположную относительному движению. Чтобы рассчитать ее проекции на координатные оси, на каждом временном шаге t нужно сформировать матрицу S, элементами которой являются расстояния s_{i,j}(t–1) между i–ой и j–ой частицами в момент t – 1. Тогда сила внутреннего трения будет равна – r(s_{i,j}(t)–s_{i,j}(t–1))/dt, где s_{i,j}(t) – расстояние между i–той и j–той частицами в момент t, r – коэффициент внутреннего трения, а выражение в скобках пропорционально скорости относительного движения этих частиц [2].
Используется программа PR–1. В ней последовательно перебираются все частицы и для каждой определяются проекции равнодействующей всех действующих сил (включая силу тяжести). После этого вычисляются проекции ускорения, скорости и координаты каждой частицы в следующий момент t+1. Результаты моделирования представлены на рис. 1.
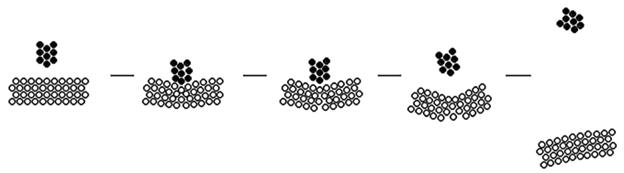
Задача 2. Тело кубической формы находится в невесомости и взаимодействует с частицей известной массы так: 1) частица отлетает от одной из его вершин, двигаясь вверх; 2) движущаяся частица соударяется с одной из вершин куба. Считая, что движение кубика плоское, необходимо рассчитать состояние системы в последующие моменты времени.
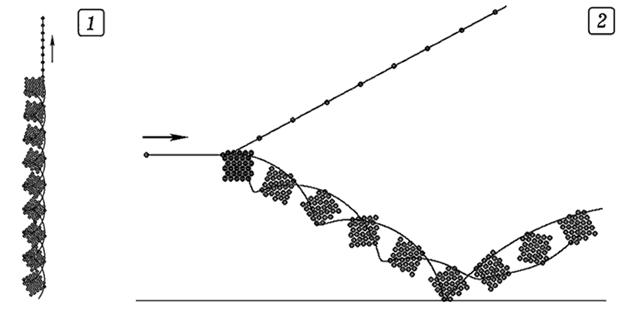
Рис. 2. Частица отлетает от одной из вершин куба. Частица сталкивается с кубом; куб отскакивает от поверхности.
Задача решается аналогично. При моделировании взаимодействия частицы с первоначально покоящимся кубом получаются результаты, представленные на рис. 2.1. Если частица отлетает от одной из его вершин, двигаясь вверх, то в соответствии с законами сохранения импульса и момента импульса, центр масс куба начнет двигаться вниз, а сам куб –– вращаться. Когда движущаяся частица соударяется с одной из вершин куба, в общем случае происходит нецентральный удар; частица и куб разлетаются (рис. 2.2). На рисунках также показаны траектории движения двух максимально удаленных точек тела. Чтобы куб сохранял свою форму, необходимо увеличить коэффициенты в выражении для силы упругости и вязкого трения. При упругом соударении частицы куба с горизонтальной поверхностью изменяется знак вертикальной проекции скорости.
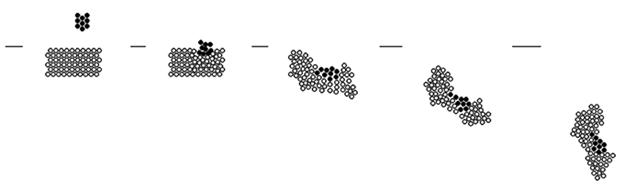
Задача 3. Горизонтальная балка закреплена за левый конец, а правый конец нагружен. Центральная часть балки имеет дефекты, уменьшающие ее прочность. Промоделируйте деформацию балки, разрушение и движение ее частей. Все точки балки перемещаются параллельно вертикальной плоскости (движение плоское).
Балку представим в виде совокупности частиц шарообразной формы, расположенных в плоскости XOY и взаимодействующих друг с другом с силами притяжения и отталкивания. Кроме того, при относительном движении частиц возникает сила вязкого трения. По условию коэффициент жесткости в центральной части балки несколько меньше среднего; частицы, расположенные вблизи правого конца имеют большую массу. Результаты моделирования представлены на рис. 3. Видно, что под действием силы тяжести балка деформируется, разламывается на две части, одна остается на месте, а другая падает вниз и соударяется с горизонтальной поверхностью.
Задача 4. На массивную мишень налетает снаряд и происходит частично упругое или абсолютно неупругое взаимодействие. Промоделируйте это явление, используя метод больших частиц. Силой тяжести пренебречь.
Результат моделирования частично упругого удара при достаточно большой массе мишени представлен на рис. 4. Видно, что сразу после удара мишень деформируется и “отталкивает” снаряд. После столкновения оба тела возвращаются к своей первоначальной форме. В программе исключены силы притяжения, действующие между частицами снаряда и мишени, поэтому снаряд отлетает от мишени.
Если уменьшить коэффициенты упругости и вязкости, а также сделать так, чтобы модель учитывала силы притяжения, возникающие при сближении частиц снаряда и мишени, то удастся промоделировать абсолютно неупругий удар (рис. 5). После взаимодействия деформированные снаряд и мишень движутся с равными скоростями и вращаются в соответствии с законами сохранения импульса и момента импульса.
Задача 5. Вокруг планеты вращается спутник. Планета создает на поверхности спутника приливную волну, которая его деформирует и изменяет скорость вращения. В результате спутник начинает вращаться в направлении своего орбитального движения. Промоделируйте это явление.
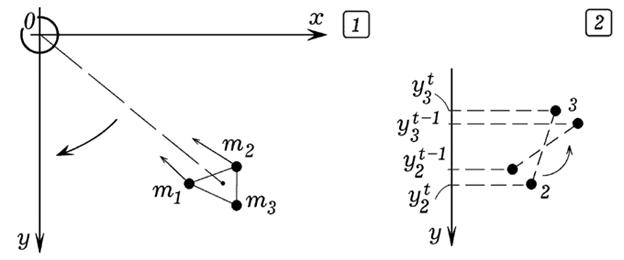
Эта задача проанализирована в книге [5, с. 17–22]. Требуется рассмотреть движение и взаимодействие трех частиц, моделирующих спутник, которые движутся вокруг планеты, расположенной в начале координат O (рис. 6.1). Со стороны планеты на каждую из трех частиц действует сила гравитационного притяжения. Частицы также притягиваются друг к другу, а при сближении взаимодействуют с силами упругости. При относительном движении между частицами действует сила вязкого трения.
Программа [2] позволяет рассчитать положение планеты и трех частиц, моделирующих спутник, а также строит график зависимости угловой скорости вращения спутника w от времени. Начальные условия заданы так, что при t = 0 спутник вращается вокруг планеты по часовой стрелке, а вокруг своей оси –– в противоположном направлении, то есть против часовой стрелки. В результате движения в неоднородном поле планеты образующаяся приливная волна уменьшает скорость вращения спутника вокруг своей оси, а затем заставляет его вращаться в направлении орбитального движения. Чтобы вычислить угловую скорость w собственного вращения спутника выбирают любые две принадлежащие ему частицы, например, m_2 и m_3, и определяют время t’, в течение которого выполняется условие (рис. 6.2):
(y_2(t–1)–y_3(t–1))*( y_2(t)–y_3(t)) > 0.
Это неравенство перестает выполняться в момент, когда прямая, соединяющая частицы m_2 и m_3 становится горизонтальной. Соответствующее время t’ равно половине периода T, поэтому w=2*3,1415926 /w.
Получающийся график зависимости проекции угловой скорости вращения спутника от времени приведен на рис. 7. Сначала спутник вращается в сторону, противоположную направлению его орбитального движения. Видно, что угловая скорость w спутника по модулю уменьшается до нуля, изменяет свое направление, а затем растет, стремясь к некоторой постоянной величине w’. При этом ее значение совершает затухающие колебания относительно w’. Следует понимать, что в нашем случае спутник движется не по эллиптической орбите с небольшим эксцентриситетом (как Луна вокруг Земли), а по сильно вытянутой незамкнутой орбите. При этом он близко приближается к планете (в область с сильно неоднородным гравитационным полем); в этот момент приливная волна оказывает наибольшее влияние на торможение спутника и его раскручивание в прямом направлении.
Задача 6. Внутри сосуда имеется столб вязкой жидкости, касающийся его левой вертикальной стенки. Если систему предоставить самой себе, то произойдет обрушение столба жидкости. Необходимо создать двумерную модель этого явления.
Будем использовать метод больших частиц. Проекцию F_r силы взаимодействия между частицами на ось r зададим так: 1) если r > 10, то частицы не взаимодействуют: F_r; 2) если r лежит в интервале [ 7; 10 ], то частицы притягиваются: F_r = –1000; 3) если r < 7, то частицы отталкиваются: F_r = 20000. Величины r и F_r заданы в условных единицах.
Решением задачи является программа PR–2. В ней заданы начальное состояние системы (процедура Nach_uslov), учтены силы взаимодействия частиц друг с другом и со стенками сосуда (процедура Sila). Тело программы содержит цикл по времени (Repeat … until;), в котором пересчитываются проекции ускорений, скоростей и координаты 300 частиц жидкости [2].
При запуске программы PR–2 моделируется обрушение столба жидкости, которая растекается по дну сосуда к его правой стенке, соударяется с ней, образует всплеск и частично возвращается обратно (рис. 8). Через некоторое время движение прекращается. Модель допускает изменение плотности и вязкости жидкости, ускорения свободного падения и размеров сосуда.
Задача 7. На поверхность вязкой жидкости падает неоднородное тело, имеющее квадратное сечение. Необходимо рассчитать движение тела в случаях, когда средняя плотность тела больше или меньше плотности жидкости. Движение плоское.
Для построения компьютерной модели рассмотрим двумерную модель тела, состоящую из 48 частиц различной массы (рис. 9). Чтобы тело “было твердым”, то есть не меняло своей формы, необходимо исключить перемещения составляющих его частиц. Этого можно достичь, увеличив силу вязкого трения (коэффициент rs, программа PR-3), действующую между частицами.
Следует учесть, что при погружении тела в жидкость на частицы, оказавшиеся ниже уровня жидкости, действует сила Архимеда, направленная вверх (противоположно оси Oy). Если плотность тела в данной точке меньше плотности жидкости, то сила Архимеда, действующая на соответствующую частицу, превышает силу тяжести. Используется программа PR–3 [2]; результаты моделирования для тела, средняя плотность которого больше плотности жидкости, представлены на рис. 9. Тело неоднородное, у черных частиц масса в 5 раз больше чем у белых, центр масс не совпадает с центром плавучести. Тело сначала движется вниз, после взаимодействия с поверхностью жидкости начинает вращаться по часовой стрелке и погружается вглубь жидкости. Затем оно, совершая колебания, всплывает вверх. Если средняя плотность тела больше плотности жидкости, то оно будет опускаться вниз.
Задача 8. На поверхности воды плавает бревно, к концу которого привязана упругая нить с грузом известной массы. Груз поднимают до заданного уровня, а затем отпускают так, чтобы он двигался в вертикальной плоскости, проходящей через ось бревна. Необходимо рассчитать движение груза и бревна с течением времени.
Рис. 10. Движение плавающего бревна и привязанного к нему груза.
Задача решается рассмотренным выше методом; используемая программа представлена в [2]. При ее запуске бревно опускается на поверхность жидкости и погружается на глубину, при которой сила тяжести уравновешивается силой Архимеда. После этого груз, привязанный к бревну нитью заданной длины, приходит в движение. Если масса груза велика, то бревно тонет. В случае, когда груз имеет небольшую массу, он совершает колебания, вызывая движения бревна (рис. 10); через некоторое время система переходит в состояние покоя. Движение системы зависит от плотности и вязкости жидкости, плотности бревна, его объема и массы груза.
Библиографический список
- Кунин С. Вычислительная физика. – М.: Мир, 1992. – 518 с.
- Майер Р. В. Задачи, алгоритмы, программы / Р. В. Майер [Электронный ресурс]. URL: http://maier–rv.glazov.net, http://mayer.hop.ru
- Майер Р.В. Компьютерное моделирование физических явлений. – Глазов, ГГПИ: 2009. – 112 с. (http://komp–model.narod.ru)
- Поттер Д. Вычислительные методы в физике / Д. Поттер. – М.: Мир, 1975. – 392 с.
- Woolfson M.M., Pert G.J. An Introduction to Computer Simulation. – Oxford University Press, 1999. – 311 p.
Количество просмотров публикации: Please wait