Введение
В работе [1] были предложены ряд инструментов – Maple-процедур для исследования последовательности простых чисел. Данная статья продолжает развитие темы. Принятые соглашения остаются прежними: красный шрифт используется для записи команд Maple, синий шрифт и графики – результат выполнения команд.
В математике простых чисел особое место занимает знаменитая гипотеза, сформулированная выдающимся немецким математиком Георгом Фридрихом Бернардом Риманом в 1859 году, и называемая «Гипотезой Римана» [2]. Согласно этой гипотезе, характер распределения простых чисел может существенно отличаться от предполагаемого в настоящее время. Дело в том, что математикам до сих пор не удавалось точно зафиксировать наличие какой-либо системы в характере распределения простых чисел. Считается, например, что в окрестности целого числа х среднее расстояние между последовательными простыми числами пропорционально логарифму х, так что имеет мест аcимтотическая формула
p ~ k ln(k), (1)
где p – величина простого числа, k – его номер по порядку. Знак ~ в выражении (1) означает, что отношение p/(k ln(k)) с ростом k стремится к 1.
Изобразим на одной диаграмме график функции p(k) с экспериментально подобранным поправочным коэффициентом 1,16k и точечный истинных значений первых 150 простых чисел (по оси абсцисс откладывается номер простого числа, а по оси ординат – его значение).
> restart:
> N:=150:
p:=seq(ithprime(i),i=1..N):#где i – номер простого числа
a:=plot([seq([n,p[n]],n=1..N)],style=point,symbol=circle,color=blue):
b:=plot([seq([k,1.16*k*ln(k)],k=1..N)]):
plots[display]([a,b]);
Асимптотическая формула даёт хорошее приближение. И оно было бы ещё лучше, если бы в последовательности простых не встречались так называемые простые числа-близнецы – парные простые числа, разность между которыми равна 2, то есть 11 и 13, 29 и 31, 59 и 61. Эти числа более всего нарушают общую картину.
Ещё одно асимптотическое равенство впервые доказанное Карлом Фридрихом Гауссом записывается как
π(x)~x/ln(x), x→∞,
и называется в настоящее время законом распределения простых чисел. Функция π(x) в этом законе выражает количество простых чисел, меньших или равных x.
1 Проблема простых чисел-близнецов
Замечено, что все пары простых-близнецов, кроме (3,5), имеют вид 6k-1 и 6k+1, где k – натуральное число.
Построим процедуру blz(N), которая возвращает пары чисел близнецов, начиная с пары (5,7) и заканчивая парой чисел, не превышающих (N-2,N), где N – параметр процедуры. На точечном графике изображаются только эти пары чисел (по оси абсцисс откладываются номера пар). В основе процедуры лежит цикл с шагом i=6.
> restart:
blz:=proc(N)
local i,a,b,t1,t2:
t1:=NULL:t2:=NULL:
for i from 7 to N by 6 do
if isprime(i) and isprime(i-2) then lprint(i-2,i): t1:=t1,i-2:t2:=t2,i: end if:
end do:
t1:=[t1]:t2:=[t2]:
a:=plot([seq([n,t1[n]],n=1..nops(t1))],style=point,symbol=circle,color=red):
b:=plot([seq([k,t2[k]],k=1..nops(t2))],style=point,symbol=circle,color=blue):
plots[display](a,b):
end proc:
Выделим близнецов из первых 150 натуральных чисел
> blz(200);
5, 7
11, 13
17, 19
29, 31
41, 43
59, 61
71, 73
101, 103
107, 109
137, 139
149, 151
179, 181
191, 193
197, 199
Из результата видно, что простые близнецы могут образовать кластеры (скопления), например 101, 103, 107, 109. У математиков давно существовало подозрение, что такие скопления существуют и в области очень больших простых чисел, однако ни доказать, ни опровергнуть это утверждение до сих пор не удавалось. Если такие кластеры будут найдены, стойкость криптографических ключей, используемых в настоящее время, может оказаться под очень большим вопросом.
Математическое сообщество в полной мере оценило важность задачи — гипотеза Римана была признана одной из 7 важнейших научных проблем тысячелетия. Институт математики Clay в США предложил $1 млн. за ее доказательство либо опровержение. И периодически средства массовой информации, математики-профессионалы и любители сообщают о некоторых “значительных” прорывах в данной области.
2 Распределение простых чисел близнецов
Следующая процедура blz_1(N) подсчитывает число пар “близнецов”, не превышающих числа N и строит график интегральной функции распределения числа пар близнецов, не превышающих N (цикл с шагом 6).
> restart:
blz_1:=proc(N)
global M:
local m,i:
printf(“%s %s”,i,m); print():
printf(“====================”); print():
m:=0:M:=NULL:
for i from 7 to N by 6 do
if isprime(i) and isprime(i-2) then m:=m+1:
printf(“%g %gn”,i,m):
end if:
M:=M,[i,m];
end do:
lprint(“для множества чисел не превышающих”, N):
lprint(“число пар близнецов”=m):
plot([M])
end proc:
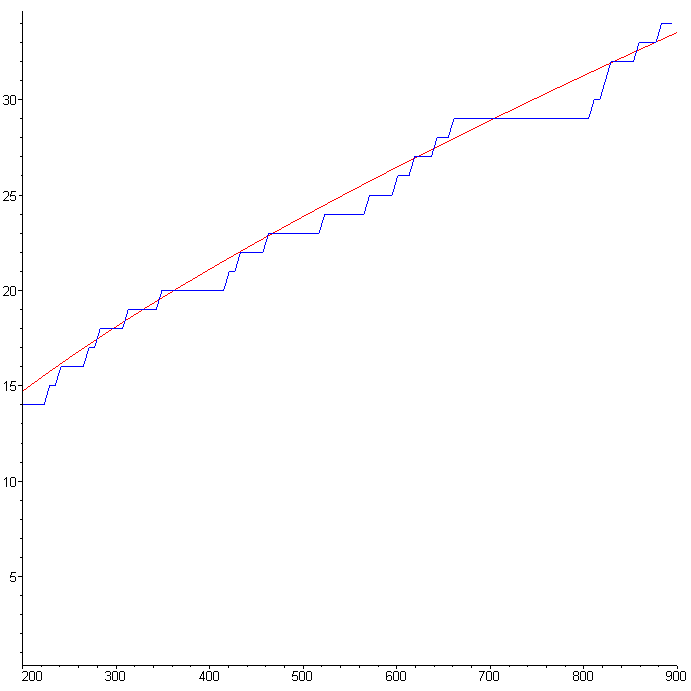
Выведем, например, значения и график функции для аргумента, не превышающего N =900:
> blz_1(900);
i m
====================
7 1
13 2
19 3
31 4
43 5
61 6
73 7
103 8
109 9
139 10
151 11
181 12
193 13
199 14
229 15
241 16
271 17
283 18
313 19
349 20
421 21
433 22
463 23
523 24
571 25
601 26
619 27
643 28
661 29
811 30
823 31
829 32
859 33
883 34
“для множества чисел не превышающих”, 900
“число пар близнецов” = 34
Наблюдаем, что число пар близнецов растёт (правда, неравномерно).
Предполагается, что пар близнецов бесконечно много, но это не доказано. По гипотезе Харди-Литтлвуда [2], количество пар простых-близнецов, не превосходящих x, асимптотически приближается к
где
- константа простых-близнецов. Произведение вычисляется по всем простым числам, начиная с тройки (это второе простое число, поэтому последовательность простых чисел, формируемая ниже, создается для для счётчика i начиная с числа 2).
Так, для 10000 множителей константа С2 равна
> n:=10000:
s:=seq(ithprime(i),i=2..n):
C2:=1:
for p in [s] do C2:=C2*(1-1/((p-1)^2)) end do:
evalf(C2);
0.6601623198
Оценим значение функции π2(x)
> pi2:=x->2*C2*int(1/(ln(t)^2),t = 2 .. x);
При x = 900, значение π2(x) равно
> ceil(pi2(900.));
43
Истинное значение функции нами было получено выше, оно равно 34. Чтобы график функции лучше совпадал с графиком истинного распределения простых близнецов на отдельных участках можно вновь ввести поправочные коэффициенты, т.к. как соотношение для π2(x) приближённое. Например, для области определения [200, 900] примем поправочный коэффициент 0,78.
> a:=plot([M],color=blue):
b:=plot(0.78*pi2(x),x=200..900):
plots[display](a,b);
Получено визуально удовлетворительное приближение.
3 Теорема Бруна
В 1919 году норвежский математик Вигго Брун исследовал ряд
где в круглых скобках раcположены суммы чисел, обратных простым близнецам [3].
Предложим процедуру для изучения свойств суммы этого ряда
> restart:
brun:=proc(n)
local s, B2, i, a:
s:=seq(ithprime(k),k=1..n+1):
B2:=NULL:
print(B2);
for i to n do
if s[i]-s[i+1]=-2 then B2:=B2,1/s[i]+1/s[i+1]:end if:
end do:
B2:=[B2]:
print(B2);
a:=plot([seq([t,sum(B2[k1],k1=1..t)],t=1..nops(B2))],style=point,symbol=circle,color=red):
sum(B2[u],u=1..nops(B2));
print(`Сумма ряда`,evalf(%));
plots[display](a):
end proc:
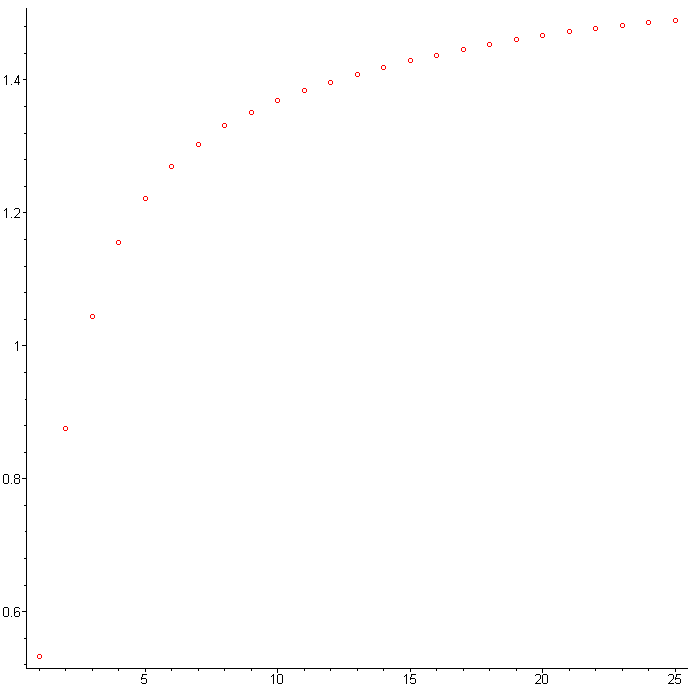
Возьмём 100 членов ряда
> brun(100);
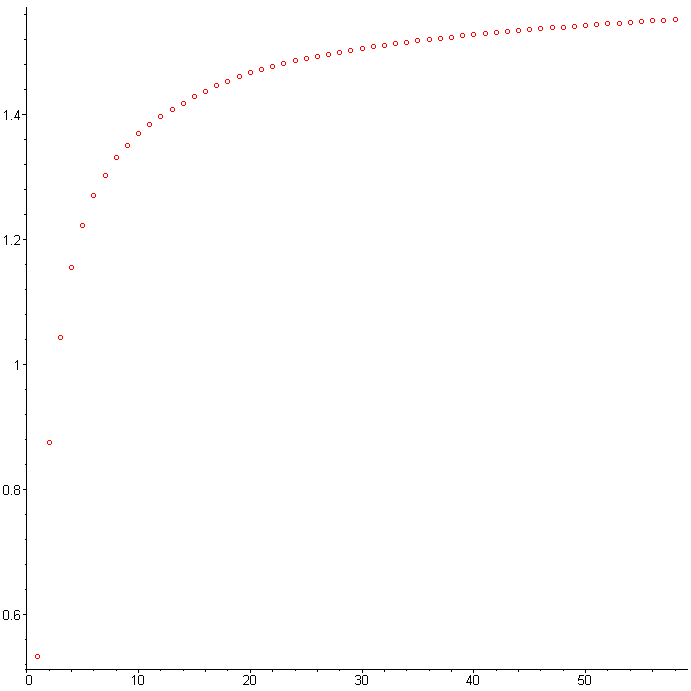
Аналогичный результат без перечисления значения сумм:
> brun(1000);
Мы наблюдаем, что график изменения суммы ряда сначала идёт резко вверх, а затем скорость роста значений существенно замедляется. В. Брун доказал, что этот ряд сходится.
Значение B2=1,902160583104 называется константой Бруна для простых-близнецов, при этом
Это означает, что если простых близнецов и бесконечно много, то они все же расположены в натуральном ряду довольно редко.
4 Классы простых-близнецов
Попробуем выделить отдельные классы простых-близнецов. Пусть в этом нам поможет следующая таблица, состоящая из 30 столбцов, предложенная в работе [4].
Соответствующая процедура, создающая такую таблицу (позиции составных чисел в ней отмечены прочерками) приводится ниже.
> Fm:=proc(Q::integer)
global M,P:
local i,j,k,w,t,m,mn,a,b:
M:=array(1..Q,1..30);
k:=0:
for i to Q do
for j to 30 do
if i=1 and j<16 then M[i,j]:=`-`
else
k:=k+1:
if isprime(k) then
M[i,j]:=k:
else
M[i,j]:=`-`
end if:
end if:
end do:
end do:
w:=[seq(2*i*Pi/30,i=1..30)];
for t to Q do
m:=[seq(M[t,j],j=1..30)];
mn[t]:=seq([m[i],w[i]],i=1..30);
end do:
P:=[seq(mn[ik],ik=1..Q)]:
print(evalm(M));
end proc:
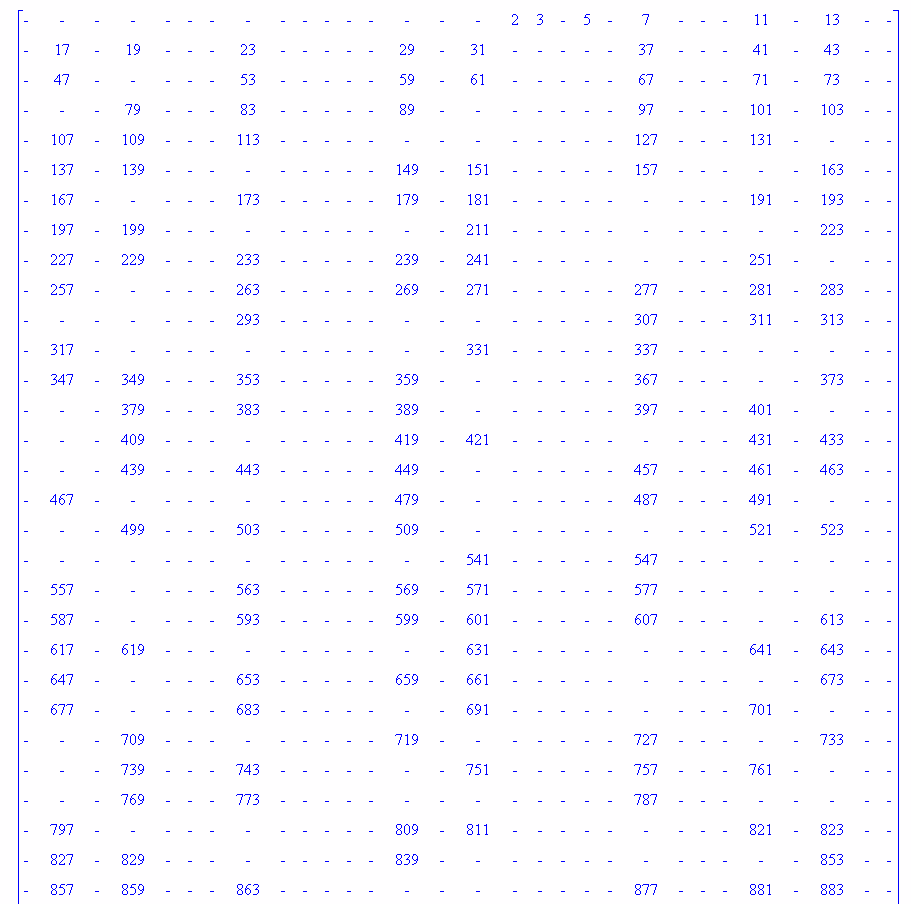
Начало натурального ряда находится в середине первой строки таблицы. Рассмотрим, к примеру, таблицу в 30 строк.
> Fm(30);
В полученной таблице можно отчётливо выделить три непересекающихся подмножества простых чисел – близнецов. Это пары чисел, которые заканчиваются на 7 и 9, 9 и 1, 1 и 3.
Известная теорема утверждает, что по модулю 30 все пары близнецов, кроме первых двух, имеют вид (11, 13), (17, 19) или (29, 31); именно эти числа стоят во главе соответствующих столбцов.
Напомним, что два натуральных числа a и b, разность которых кратна натуральному числу m (эти числа имеют одинаковые остатки при делении на m), называются сравнимыми по модулю m. Например, к одному подмножеству отнесём пары близнецов (1451, 1453) и (1481, 1483), так как для них имеем
> 1481 mod 30 = 1451 mod 30;
11=11
> 1483 mod 30 = 1453 mod 30;
13=13
Рассмотрим распределения простых-близнецов каждого из трёх подмножеств. Для этого создадим процедуру, в которой действует цикл с шагом 30, внутри которого с шагом 12 проверяются на простоту пары “близнецов”)
> restart:
tc:=proc(N)
local q,Q,r,R,s,S,a,b,c,i:
q:=0:Q:=NULL:r:=0:R:=NULL:s:=0:S:=NULL:
for i from 19 to N by 30 do
if isprime(i) and isprime(i-2) then q:=q+1:
Q:=Q,[i,q]:
end if:
if isprime(i+12) and isprime(i+12-2) then r:=r+1:
R:=R,[i+12,r]:
end if:
if isprime(i+24) and isprime(i+24-2) then s:=s+1:
S:=S,[i+24,s]:
end if:
end do:
a:=plot([Q],color=red,style=point):#на 7 и 9
b:=plot([R],color=blue,style=point):#на 9 и 1
c:=plot([S],color=green,style=point):#на 1 и 3
plots[display](a,b,c);
end proc:
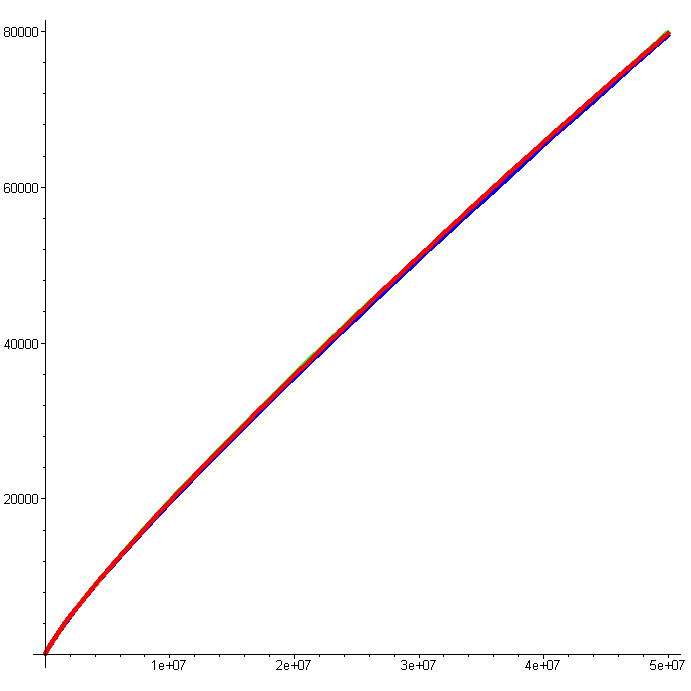
Процедура возвращает графики распределения простых-близнецов каждого из трёх подмножеств: красный цвет – близнецы, равные по модулю 17 или 19, синий – 29 или 31, зелёный – 11 или 13. Например, среди первых 10000 натуральных чисел
> tc(10000);
Судя по графику эти три распределения близки между собой. Получим график в пределах первых 50 миллионов натуральных чисел (внимание: расчёт по программе требует времени).
> tc(50000000);
Из последнего графика видно, что в пределах эти 50 миллионов находится примерно по 80 тысяч пар близнецов каждого класса. Если бесконечен ряд простых близнецов, то, по-видимому, бесконечны и данные три последовательности.
Литература
1. Смирнов В.В., Спиридонов Ф.Ф. Компьютерная математика в исследовании простых чисел. // Современные научные исследования и инновации. – Февраль, 2013 [Электронный ресурс]. URL: https://web.snauka.ru/issues/2013/02/20410
2. Диамонд Г. “Элементарные методы в изучении распределения простых чисел”, // УМН, 45:2(272) (1990), 79–114 c.
3. Трост Э. Простые числа – М.: ГИФМЛ, 1959. – 135 с.
4. Omar E. Pol. Sobre el patron de los numeros primos. Determinacion geometrica de los numeros primos y perfectos. – [Электронный ресурс]. URL: http://www.polprimos.com/
Количество просмотров публикации: Please wait