Е.В. Черепанов, к.т.н.
Введение.
В середине XIX в. У.С. Джевонсом [1,2] и Дж. Дюпюи [3] были введены базовые понятия экономической теории. Но до настоящего времени описание этих категорий носит качественный характер («спрос монотонно убывает с ростом цены», «кривая ценности товара монотонно возрастает с ростом цены и выпукла вверх» и т.п.) Однако, еще Аристотель [4] писал, что «…поступок и сознательный выбор, как принято считать, стремятся к определенному благу». И эта мысль великого античного философа в полной мере относится и к процессу торговли. А значит, есть основание считать, что взаимосвязи между основными величинами потребительского рынка поддаются функциональному описанию. А в основе количественного описания потребления и производства должны лежать некие процедуры оптимизации, обеспечивающие получение максимума выгоды совокупным продавцом и совокупным покупателем товаров.
Такая предпосылка позволила автору получить вид функциональных зависимостей между основными категориями потребления и производства (торговли) на рынке конкурентных товаров [5,6;7,гл.6]. Но остается «открытым» вопрос количественного описания монопольного рынка, который в принципе не сводится к одномерному случаю многотоварного потребительского рынка.
Дело в том, что при определении вида функций на конкурентном рынке было использовано то обстоятельство, что соотношения между ценой и объемом потребления каждого товара удовлетворяют одновременной максимизации мер выгоды продавца (прибыли) и совокупного покупателя (излишка потребителя) для каждого товара, представленного на рынке. А на монопольном рынке и цена товара, и объем предложения находится в руках производителя (продавца).
Что заставляет при количественной формализации категорий монопольного рынка исходить из иных, нежели на конкурентном рынке, предпосылок. Этой проблеме и посвящена настоящая публикация. Перед ознакомлением с ней, как кажется автору, целесообразно ознакомиться с легко доступными статьями [5,6].
-
Категории монопольного потребительского рынка
На потребительском (в частности, монопольном) рынке издержки продавца (затраты производителя) для любой единицы времени (день, квартал, год) всегда выражаются [8;9,гл.6] в виде 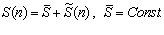 . (1.1)
. (1.1)
Смысл этого заключен в том, что полные издержки S в единицу времени равны сумме постоянных издержек 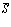 , не зависящих от объема продаж, и пере-менных издержек
, не зависящих от объема продаж, и пере-менных издержек 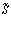 , зависящих от потребления (а не предложения продавца !)
, зависящих от потребления (а не предложения продавца !)
Потреблением n мы будем называть фактически реализованный за единицу времени спрос на товар. А обсуждение будем вести в терминах потребления, а не спроса покупателей и предложения продавца, что принято при традиционном изложении основ теории рынка. Такая позиция связана с тем, что эмпирически спрос проявляется в виде потребления, а предложение продавца измерению не поддается. Следовательно, везде далее речь идет исключительно об издержках продавца на фактически проданные за данную единицу времени товары.
Издержки 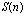 монотонно возрастают функцией с ростом потребления n, причем при
монотонно возрастают функцией с ростом потребления n, причем при 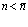 предложение отсутствует (прибыль отрицательна) и
предложение отсутствует (прибыль отрицательна) и 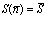 . Потребление n монотонно убывает с ростом цены р. Стоимость потребленного товара равна V(n ) = np(n) = pn(р). (1.2)
. Потребление n монотонно убывает с ростом цены р. Стоимость потребленного товара равна V(n ) = np(n) = pn(р). (1.2)
Под потребительской ценой
р данного товара мы будем понимать среднестатистическое отношение количества отданных за него денег (в единицу времени) к количеству купленного товара: p = V / n. По смыслу (для многотоварных рынков), потребительская цена совпадает с равновесной ценой (при традиционном изложении теории рынка [8,9]), когда значения совокупного спроса равно предложению продавца. При значениях цены, выше некоторого значения 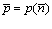 , стоимость товара равна нулю (исчезает спрос).
, стоимость товара равна нулю (исчезает спрос).
Прибыль продавца выражается в виде P(n) = V(n) - S(n). (1.3)
При ценах выше 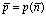 прибыль равна нулю:
прибыль равна нулю: 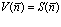 , в точке
, в точке 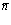 монотонно возрастающая функция
монотонно возрастающая функция 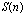 пересекает кривую
пересекает кривую 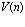 . Допустимыми являются значения цены и соответствующего потребления в диапазонах
. Допустимыми являются значения цены и соответствующего потребления в диапазонах 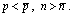
В основе теории потребление лежат важнейшие понятия полезности товара и излишка потребителя. Экономический смысл категории полезности товара, которая была введена в экономику У. Джевонсом [1,2], заключается в том, что каждый товар приносит некоторое удовлетворение, определенные «блага» совокупному покупателю. А ценность товара U – это выражение полезности в деньгах. При этом деньги выступают как единая шкала измерения ценности, позволяющая сравнивать полезность товаров различной природы и качества.
Функцией ценности товара 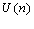 на монопольном рынке является отображение
на монопольном рынке является отображение 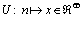 , монотонно возрастающее с ростом n. Функция U(n) выпуклая вверх, что обусловлено законом убывания полезности: покупка (k + 1)-й единицы товара всегда менее полезна, чем была покупка k-й единицы.
, монотонно возрастающее с ростом n. Функция U(n) выпуклая вверх, что обусловлено законом убывания полезности: покупка (k + 1)-й единицы товара всегда менее полезна, чем была покупка k-й единицы.
Потребительский излишек (или излишек потребителя) W(n), введенный в экономику Ж. Дюпюи [3], является мерой выгоды совокупного покупателя от приобретения данного товара в заданном объеме n. Количественно потреби-тельский излишек выражается разностью между ценностью (равной той максимальной сумме U, которую совокупный покупатель готов был заплатить за данный объем товара) и фактическими затратами на его приобретение V:
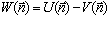 . (1.4)
. (1.4)
Ж. Дюпюи писал [3] «Окончательная полезность продукта («потреби-тельский излишек» – авт.) выражается в виде разности между жертвой, которую покупатель согласен принести, чтобы приобрести этот продукт, и покупной ценой, которую он должен заплатить за него… В торговле реальна та полезность, которую покупатели согласны оплачивать». Соотношение (3.2) определяет смысл процесса обмена товаров на деньги за единицу времени. За объем товара n совокупный покупатель выплачивает стоимость V. Взамен покупатели удовлетворяют некоторые свои потребности U и получают выгоду, которая равна излишку совокупного (!) потребителя W. На монопольном рынке, очевидно, продавец «недополучил» сумму, равную излишку потребителя вида
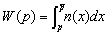 , (1.5)
, (1.5)
где n(p) – кривая потребления (совокупного спроса) на товар. Из (1.5) ясно, что потребление на монопольном рынке равно 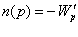 . (1.6)
. (1.6)
Интегрируя по частям выражение (1.5), получаем:
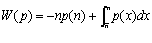 (1.7)
(1.7)
Величина выручки продавца от продажи товара V была бы равна его ценности U в том случае (W=0), если бы каждый покупатель платил за купленную им часть товара максимальную из приемлемых для него цен.
Из соотношений (1.2), (1.4) и (1.7) следует, что 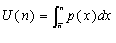 .
.
(1.8)
Откуда непосредственно получаем, что 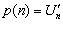 , (1.9)
, (1.9)
т.е. на монопольном рынке предельная полезность товара совпадает с его ценой.
-
Критерий максимизации прибыли продавца (производителя)
Для стоимости товара (затратах совокупного потребителя) можно записать:
 . (2.1)
. (2.1)
Представим удельные издержки продавца (затраты производителя) в виде
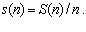 (2.2)
(2.2)
Далее мы будем говорить об одном продавце и совокупном покупателе. Подразумевая, что правомерно говорить и об одном производителе на оптовом рынке, поскольку с формальной точке зрения издержки продавца и затраты производителя эквивалентны, отличаясь только по структуре и своей природе.
Совокупный спрос, как функция 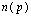 , определяет количество товара на монопольном рынке, которое совокупный покупатель хочет и может приобрести в заданных условиях. Функция потребления – это количество реально покупаемых (за единицу времени) товаров (в зависимости от цены). Потребление – это реализованный (за единицу времени) спрос. Под «единицей времени» понимается период, за который фиксируется состояние рынка.
, определяет количество товара на монопольном рынке, которое совокупный покупатель хочет и может приобрести в заданных условиях. Функция потребления – это количество реально покупаемых (за единицу времени) товаров (в зависимости от цены). Потребление – это реализованный (за единицу времени) спрос. Под «единицей времени» понимается период, за который фиксируется состояние рынка.
Введем новые переменные вида
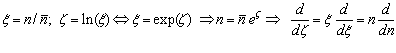 (2.3)
(2.3)
Ясно, что переменная «кси» является безразмерной величиной, сравнивающей текущий объем потребления с его минимально допустимым значением. А через величину «дзэта» мы в дальнейшем получим более компактные математические выражения для количественных взаимосвязей между категориями рынка.
В силу (2.1) можно записать 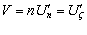 . (2.4)
. (2.4)
Основой наших дальнейших рассуждений служит мысль У.С. Джевонса [2] о том, что законы экономики «…носят настолько сложный характер, что проявляются только для совокупностей и должны изучаться методом средних». Что в «переводе» на современный язык может быть сформулировано в виде: «Экономические законы носят вероятностный характер и должны изучаться статистическими методами». А это значит, что объективно совокупный спрос проявляется в форме потребления товара за единицу времени. Потребление имеет смысл математического ожидания для распределения совокупного спроса на товар. Кривая индивидуального спроса отдельно взятого покупателя может иметь различный (и даже весьма «экзотический») вид, но кривая совокупного спроса – объективна и поддается измерению.
Общепринято [8,9], что целью продавца является получение максимально большой прибыли (за исключением некоторых частных задач: захвата нового сегмента рынка, вытеснения с рынка данного конкурента и т.п.) Например, Г. Саймон писал: «В теории фирмы основополагающей является гипотеза о стремлении предпринимателя максимизировать свою прибыль» [10].
Существует биективное отображение между переменными n и ς. Следовательно, критерий максимизации прибыли можно представить в виде
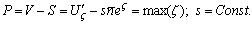 . (2.5)
. (2.5)
Удельные издержки 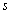 вида (2.2) зависят от n (и, следовательно, от времени). Но при краткосрочном рассмотрении потребительского рынка (за единицу времени, когда его параметры неизменны) удельные издержки правомерно считать константой [9, гл.6]. Критерий (2.5) приводит к условиям
вида (2.2) зависят от n (и, следовательно, от времени). Но при краткосрочном рассмотрении потребительского рынка (за единицу времени, когда его параметры неизменны) удельные издержки правомерно считать константой [9, гл.6]. Критерий (2.5) приводит к условиям
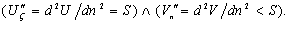 (2.6)
(2.6)
Будем исходить из того, что состояние рынка
определено не только совокупным спросом, но и значениями издержек продавцов. Но тогда оптимальная торговля должна обеспечивать выполнение условий (2.6) в каждую единицу времени. При этом, как следует из (2.6) и (2.4), с необходимостью всегда выполняется соотношение вида 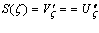 . (2.7)
. (2.7)
Отсюда для совокупной стоимости купленного товара можно записать:
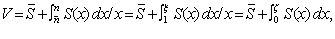 (2.8)
(2.8)
где постоянные издержки продавца 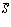 равны
равны 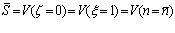 .
.
Интегрируя выражение (2.8) по частям, получаем соотношение вида
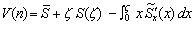 , (2.9)
, (2.9)
-
Издержки продавца (затраты производителя)
Представим стоимость в виде V = U – V. В качестве подлежащей проверке гипотезы, учитывая выражение (2.9), примем следующие соотношения:
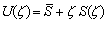 ; (3.1)
; (3.1)
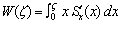 . (3.2)
. (3.2)
Эти выражения справедливы, как доказано в работе [6], для каждого товара на конкурентном потребительском рынке. Можно полагать, что они справедливы и для монопольного рынка, что предстоит формально обосновать.
В силу (2.4) запишем выражение вида
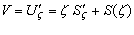 (3.3)
(3.3)
Сравнив соотношение (3.3) с соотношением (2.8), получаем уравнение вида
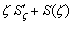
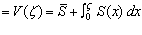 . (3.4)
. (3.4)
Продифференцировав выражение (3.4), получаем дифференциальное уравнение
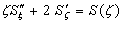 . (3.5)
. (3.5)
Использовав результат [11, п.2.2.103], общее решение дифференциального уравнения (3.5) запишем в виде цилиндрической функции 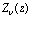 (минус первого порядка) от мнимого аргумента [12,XII.А] вида
(минус первого порядка) от мнимого аргумента [12,XII.А] вида
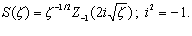 (3.6)
(3.6)
Для цилиндрических функций неотрицательного целого порядка ν = n верно выражение [12,XII.А.1]
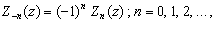 (3.7)
(3.7)
где z – комплексное число. Используя представление цилиндрической функции 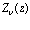 через функции Бесселя
через функции Бесселя 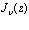 и Неймана
и Неймана 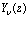 [12,XII.А], получаем общее решение дифференциального уравнения (3.5) над полем комплексных чисел
[12,XII.А], получаем общее решение дифференциального уравнения (3.5) над полем комплексных чисел
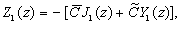 (3.8)
(3.8)
где 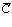 и
и 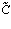 – комплексные константы. Избыточно общее выражение для функции издержек продавца (3.8) на монопольном рынке, учитывая (3.6), запишем в виде
– комплексные константы. Избыточно общее выражение для функции издержек продавца (3.8) на монопольном рынке, учитывая (3.6), запишем в виде
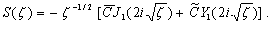 (3.9)
(3.9)
Ясно, что определение функции затрат (издержек) над полем комплексных чисел не имеет реального экономического смысла, в связи с чем нам предстоит привести выражение (3.9) к некоторой функции, области определения и прибытия которой являются полем действительных неотрицательных чисел.
-
Представления издержек продавца (затрат производителя)
Функция Неймана целого первого порядка 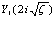 , входящая в соотношение (3.9), может быть определена [12,XIII.А.2] в виде
, входящая в соотношение (3.9), может быть определена [12,XIII.А.2] в виде
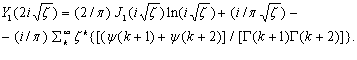 (4.1)
(4.1)
где 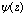 - логарифмическая производная гамма-функции [12,V.B]:
- логарифмическая производная гамма-функции [12,V.B]: 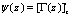 .
.
Но логарифм мнимого аргумента 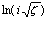 , входящий в соотношение (4.1), выражается в виде знакопеременного ряда и, следовательно, выражение вида
, входящий в соотношение (4.1), выражается в виде знакопеременного ряда и, следовательно, выражение вида 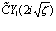 всегда определяет комплексное число с ненулевой мнимой частью. Отсюда следует, что в выражении (3.9) нам необходимо положить
всегда определяет комплексное число с ненулевой мнимой частью. Отсюда следует, что в выражении (3.9) нам необходимо положить 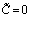 .
.
Использовав представление функции Бесселя 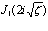 в виде ряда [12,XIII.А.2]
в виде ряда [12,XIII.А.2]
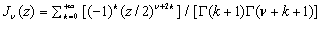
и положив 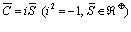 , из соотношения (3.9) получаем итоговый вид функции издержек продавца (затрат производителя):
, из соотношения (3.9) получаем итоговый вид функции издержек продавца (затрат производителя):
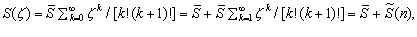 (4.2)
(4.2)
где 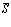 и
и 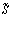 - переменные и постоянные издержки [9, гл.6] соответственно.
- переменные и постоянные издержки [9, гл.6] соответственно.
И по смыслу нашего изложения ясно, что в 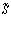 учитываются только переменные издержки, связанные с купленным товаром. Продавец, как и производитель, может за данную единицу времени иметь избыточные издержки, большие, чем
учитываются только переменные издержки, связанные с купленным товаром. Продавец, как и производитель, может за данную единицу времени иметь избыточные издержки, большие, чем 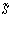 (конъюнктурные моменты, сезонность работ и т.п.) Но эта часть издержек не учитывается в величине
(конъюнктурные моменты, сезонность работ и т.п.) Но эта часть издержек не учитывается в величине  за данную единицу времени.
за данную единицу времени.
Для гамма-функции любого комплексного аргумента справедливо условие [12,V.А] 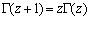 , а для натуральных аргументов верно:
, а для натуральных аргументов верно: 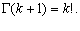
Используем определение модифицированной функции Бесселя [12,XIII.B] 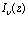 вида
вида 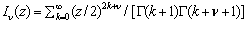 . Модифицированная функция Бесселя ν-го порядка может быть представлена [11,с.279] в интегральном виде
. Модифицированная функция Бесселя ν-го порядка может быть представлена [11,с.279] в интегральном виде
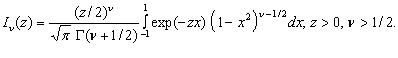
Отсюда следует, что функцию издержек можно записать в виде
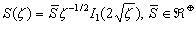 , (4.3)
, (4.3)
Для производных издержек (затрат) справедливы соотношения вида
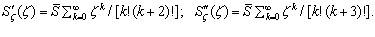 (4.4)
(4.4)
Стоимость товара, учитывая выражения (2.8) и [13, п.5.2.10.1], имеет вид
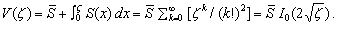 (4.5)
(4.5)
Следовательно, цена товара на монопольном рынке, учитывая (2.6), имеет вид
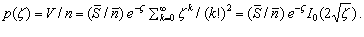 (4.6)
(4.6)
Отметим, что, как и должно быть: 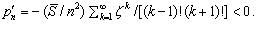
Учитывая соотношение (3.1), ценность купленного товара выражается в виде
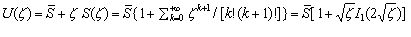 . (4.7)
. (4.7)
Потребительский излишек выразится в виде
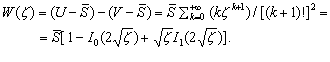 (4.8)
(4.8)
Правомерность гипотезы (3.1-2) следует из того, что вычисления по формуле (3.2) вида 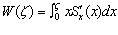 также приводят к выражению (4.8) для W.
также приводят к выражению (4.8) для W.
Для величины прибыли P правомерно записать:
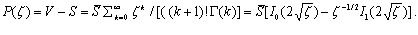 (4.9)
(4.9)
Для производной функции прибыли правомерно записать:
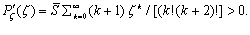
Следовательно, с ростом потребления прибыль (достаточно медленно) растет. Из последнего выражения правомерно записать:
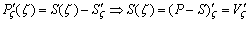 ,
,
Что полностью согласуется с исходной предпосылкой вида (2.7).
Выводы.
На любом потребительском рынке продавец (производитель) стремится к получению максимума прибыли. И, как показано выше, на монопольном рынке цена товара равна его предельной ценности. Используя эти факты, удалось получить вид функциональных зависимостей между основными категориями торговли (производства) и спроса (потребления) для монопольного рынка.
Библиографические ссылки
-
Jevons W.S. Notice of a general mathematical theory of political economy. – British Assoc. For the Advancement of Science. // Report of the 32 Meeting Transaction of the Sections. L.J. Murray, 1862, р.158-159.
-
Jevons W.S. Brief of a general mathematical theory of political economy. // Journal of the Statistical Society of London. 1866, XXIX, № 2, р. 282-287.
-
Dupuit J. De la mesure de l`utilite des travaux publics. // Annales des ponts et chaussees, 1844, VIII, ser. 2, р. 332-375.
-
Аристотель. Никомахова этика. // Философы Греции. Сер.: Антология мысли. М.: Эксмо-пресс, 1999, с. 793-1026.
-
Черепанов Е.В. О количественном описании категорий микроэкономики. //
Современные научные исследования и инновации. Электронный научный журнал. (ISSN 2223-4888). Дек. 2011. (https://web.snauka.ru/issues/2011/12/5666 ). -
Черепанов Е.В. К вопросу описания количественных взаимосвязей между категориями потребления и производства. // Гуманитарные и социальные науки. Электронный журнал. (ISSN 2070-1403). Ростов на Дону: ЮФУ, 2012, № 2, с. 313-333. (http://hses-online.ru/2012/02/22_00_01/33.pdf).
-
Черепанов Е.В. Нетрадиционные вероятностно-статистические методы для социально-экономических и социологических исследований. М.: Спутник Плюс, 2012. (ISBN 978-5-9973-1707-2).
-
Пиндайк Р., Рубинфельд Д. Микроэкономика / Пер. с англ. М.: Дело, 2000.
-
Ковалев С.В. Экономическая математика. М.: Крокус, 2010.
-
Simon H. Theories of decision-making in economics and behavioral science. // Microeconomics: Selected Reading. Ed. by E. Mansfield. N.Y., 1971.
-
Зайцев Ф.В., Полянский А.Д. Справочник по линейным обыкновенным дифференциальным уравнениям. М.: Факториал, 1997.
-
Янке Е., Эмде Ф., Леш Ф. Специальные функции. / Пер. с нем. М.: Наука, 1968.
-
Прудников А.П. и др. Интегралы и ряды. М.: Наука, 1981.
Количество просмотров публикации: Please wait


