Введение
Импровизация (итал. improvisazione, от лат. improvisus — неожиданный, внезапный) — исторически наиболее древний тип музицирования, при котором процесс сочинения музыки происходит непосредственно во время её исполнения.
Первоначально импровизация характеризуется канонизированным набором мелодических и ритмических элементов, варьированное сочетание которых не сковано канонами и обусловливаетархитектоническую незамкнутость формы.
Импровизация господствует в фольклоре, музыке неевропейских культур, она получила широкое распространение также на раннем этапе европейской профессиональной музыки, когда запись была приблизительной и неполной (невмы, крюки), а кодификация норм композиции, ведущая к замкнутой форме, затрагивала лишь коренные свойства музыки (церковные лады), оставляя их конкретное воплощение в напевах отчасти на долю импровизации. Дифференциация системы музыкальных жанров и соответствующих нормативов привела в XI веке к отделению исполнительства от композиции. Однако импровизация сохранилась в виде исполнительского искусства орнаментики, которое подразумевалось при неполной нотной фиксации опуса.
Возникновение индивидуальных, внутренне законченных, несводимых к жанровым нормам музыкальных произведений потребовало их точной и полной записи, устраняющей произвол исполнителя. Вместо импровизации кристаллизовалось искусство интерпретации. В творчестве композитора и интерпретатора импровизация существует в «снятом» виде: на подготовительном этапе формирования музыкальных образов; в нюансах исполнения авторского текста.
В XVII—XVIII вв. исполнительская импровизация сохранилась в традиции виртуозных фантазий, сольных каденций инструментальных концертов, в хоральных обработках (и даже фугах) у органистов. В конце XVIII — 1-й пол. XVIII вв. в аристократических салонах и на концертной эстраде импровизация была распространена в качестве специального номера программы у виртуозов.
В XX веке импровизация возродилась в фольклорном по генезису искусстве джаза, а также в некоторых прикладных областях музыкальной культуры (музыкальные иллюстрации к «немым» кинофильмам в нач. XX века, музыкально-воспитательных упражнения для детей Э. Жак-Далькроза, К. Орфа). С 1950-х гг. импровизация стала опорным принципом в т. н. открытых формах музыки авангарда и неоавангарда. Некоторые музыкальные жанры сохранили названия, указывающие на их генетическую связь с импровизацией (фантазия, прелюдия, импровизация). Современные композиторы продолжают использовать импровизацию в своих сочинениях.
1 Проблемы импровизации
При импровизации в музыке – получении нового в музыке основная проблема-это сыграть ноты в необходимой тональности – то есть другими словами соблюдение определенной гармонии, хотя в музыке есть переходы между тональностями, допускается порой играть ноты не из своей тональности или сам вид гармонии начинает отличаться –
мелодический или еще какой – нибудь вид минора или мажора, при этом тональность одна, но отличаются повышением или понижением какой-либо ступени в гармонии. И при этом укладываясь в такт-то есть должна быть определенная длительность нот, чтобы соблюдалась определенная размерность в музыке. Также есть необходимость приходить в
определенные моменты к тонике – основной тон какой либо гармонии.
2 Математическое описание проблемы. Выбор нежелательного эффекта, параметров катастрофы типа сборки
V = x4 + ax2 + bx (1)
Формулу (1) можно использовать как простейшую математическую модель описания некоторого явления, процесса, системы, в которых имеется минимум потенциальной функции E(x). Если удачно назначить потенциальную функцию и выбрать из множества факторов, описывающих сложное явление (процесс или систему), всего только три - x,a,b, то получим модель, описывающую суть явления В изобретательской задаче никаких проблем с удачным выбором нет.
Поэтому потенциальной функцией E(x) назначим нежелательный эффект, остальная тройка - x,a,b- характеризует изделие, инструмент и икс-элемент соответственно.
Пусть x - свойство изделия, которое может быть измерено какой-нибудь подходящей физической величиной,y=a/d - свойство инструмента, которое тоже может быть измерено какой-нибудь подходящей физической величиной,z=c/e - свойство икс-элемента, которое тоже может быть измерено какой-нибудь подходящей физической величиной,d и e - коэффициенты, выравнивающие физические размерности величин x,a,b. Тогда формулу (1) можно записать в виде
E(x) = (0,25 x4 - 0,5 d y x2 - e z x)f (2)
где f – коэффициент, выравнивающий физическую размерность величины E(x). Приведение формулы (1) к виду (2) называется масштабированием катастрофы.
Рассмотрим первую из трех проблем – соблюдение определенной гармонии.
Вообще в качестве решения проблемы можно было бы сделать инструмент с одной определенной гармонией-тональностью и импровизируй себе на здоровье, но с другой стороны этого ограничит количество и качество - разнообразие произведений, которых можно будет сыграть на данном инструменте. Порой музыкальные произведения не ограничиваются одной тональностью, такие произведения тогда вообще будет нельзя сыграть на таком инструменте.
Нежелательный эффект будем описывать катастрофой типа сборки :
E(x) = (0,25 x4 - 0,5 dyx2 -ezx) (2)
В качестве изделия у нас выступает музыкальный инструмент- для конкретики пусть это будет какой-либо струнный инструмент-гитара, балалайка, домра, скрипка.
В качестве инструмента выступает, конечно, же руки человека.
E(x)- нежелательный эффект, процент нот сыгранных не попадая в нужную тональность, то есть выпавших из гармонии.
x - свойство изделия, которое может быть измерено какой-нибудь подходящей физической величиной – а именно высота звука:
Высота звука, качество звука, определяемое человеком субъективно на слух и зависящее в основном от его частоты, т. е. от числа колебаний в секунду. С ростом частоты В. з. повышается. В небольших пределах В. з. изменяется также в зависимости от громкости звука и от его тембра. Высота сложных звуков определяется частотой основного тона, вне зависимости от соотношения между его амплитудой и амплитудой более высоких слагающих.
Таким образом, высота звука будет характеризоваться определенной частотой в Гц или с-1
За свойство инструмента y выберем либо площадь контакта руки человека с инструментом, либо скорость игры, либо силу, с которой действуют на инструмент.
Но с практической точки зрения – сложно импровизировать при больших темпах в музыке, так как человеческое восприятие и осознание того, что он делает, спадает по экспоненте от скорости игры. А следовательно возникают ошибки при игре, и получается нарушение гармонии.
Поэтому за свойство инструмента y выбираем скорость игры – она характеризуется количеством нот в секунду. Количество нот это безразмерная величина. Таким образом, размерность получается опять с-1
Коэффициент d должен быть также с-1 чтобы иметь возможность складывать первый и второй член в формуле 2.
Далее выберем коэффициент e безразмерным, тогда свойство z икс- элемента должно иметь физическую размерность с-3
3 Моделирование исходной системы
Таблица 2 – Частотные диапазоны музыкальных инструментов
|
Инструмент |
Частотный диапазон |
| Скрипка |
196 Гц до 2100 Гц |
| Контробас |
41 Гц до 260 Гц |
| Акустическая гитара |
82 Гц до 1175 Гц |
| Электрическая гитара |
82 Гц до 1570 Гц |
| Труба |
160 Гц до 1175 Гц |
| Туба |
29 Гц до 440 Гц |
| Рояль |
27 Гц до 4200 Гц |
| Флейта (малая) |
587 Гц до 4200 Гц |
| Гобой |
247 Гц до 1400 Гц |
| Кларнет |
147 Гц до 1570 Гц |
| Литавры |
73 Гц до 130 Гц |
| Электрическая бас-гитара |
41 Гц до 250 Гц |
| Альт |
130 Гц до 1050 Гц |
Как видно из таблицы частотный диапазон большинства инструментов лежит в пределах 0 -4,2 кГц. Это даст нам числовые значения для x
3.1 Статическая модель технического противоречия
E(x) =(0,25x4 – 0,5 dyx2 – ezx). (3)
Если учесть:
· e=1
· d=1 с-1
· y=λ
· z=µ
то перейдем к нашему удобному представлению статической модели технического противоречия:
E(x,λ) = 0.25x4 – 0.5 λx2 - µx,
где x – состояние инструмента,
![]() – мощность конфликта,
– мощность конфликта,
![]() – влияние Х-элемента.
– влияние Х-элемента.
Для данной задачи выберем следующие определения этих величин:
x – высота звука [ кГц] =[1000с-1],
![]() – скорость игры –количество нот в секунду [1000с-1],
– скорость игры –количество нот в секунду [1000с-1],
![]() – влияние Х-элемента
– влияние Х-элемента
[с-3].
Потенциальная функция обозначает процент нот при импровизации, которые были сыграны не попадая в тональность. То есть процент ошибок от общего числа.
Тогда размерность E = [%]. Тогда в каноническую форму потенциальной функции необходимо ввести константу с, которая обозначает процент неработоспособности в прототипе. Допустим изначально с = 5 [%].
Также введем коэффициент пропорциональности t
![]() для верности расчета.
для верности расчета.
Тогда потенциальная функция будет иметь вид:
E(x,λ) = (0.25x4 – 0.5 λx2 - µx) t +c
Пусть xср = 1 [1000с-1],
xм = 0.5[1000с-1],
хб =2,5 [1000с-1], xмм = 0 [1000с-1],
хбб = 4 [1000с-1];
λ = (хб – xм)2/4 = 1[1000с-1], с = 5 [%].
![]() 0.384[1000с-3];
0.384[1000с-3];
Сдвинем начало координат по ОХ на xср = 1 (высота звука в прототипе) для исключения отрицательных значений .
Рассмотрим случай до конфликта(λ<0), когда λ=-1, µ = 0 , с=5, t=1000 тогда
Потенциальная функция системы до конфликта:
E(x,λ) = (0.25(x-1)4+ 0.5 (x-1)2)*1000+5

Рисунок 1 – Потенциальная функция системы до конфликта
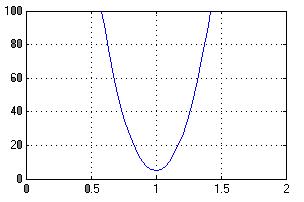
Рисунок 2 – График зависимости ошибок при импровизации от высоты звука инструмента до катастрофы
Если λ<0, то она трактуется как запас устойчивости прототипа. Этот запас устойчивости характеризует психологическую инерцию изобретателя.
Потенциальная функция системы после конфликта :
E(x,λ) = (0.25(x-1)4– λ (x-1)2 -µ(x-1)) t+5
Промоделируем поведение прототипа после конфликта:
E(x,λ) = (0.25(x-1)4-0.5 (x-1)2- 0.384(x-1)) *1000+5

Рисунок 3 – Потенциальная функция прототипа после конфликта
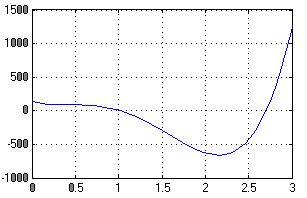
Рисунок 4 –График зависимости ошибок при импровизации от высоты звука инструмента после катастрофы
Для усиления конфликта выбираем крайнее состояние инструмента – очень большое отверстие хбб = 4 [1000с-1]
и очень маленькое xмм = 0 [1000с-1],
λ = (хбб – xмм)2/4 = 4 [1000с-1].
![]() [ 1000с-3 ];
[ 1000с-3 ];
![]() [ 1000с-3 ]
[ 1000с-3 ]
E(x,λ) = (0.25(x-2)4 – 2 (x-2)2 -3.079(x-2)) t +5
Процент ошибок при импровизации в системе после преобразования в новое E(x,λ)=1%, теперь найдем константу t:
t=(1-5)/(0.25(4-2)4 – 2 (4-2)2 -3.079(4-2))= 0.393778 тогда
E(x,λ) = (0.25(x-2)4 – 2 (x-2)2 -3.079(x-2)) 0.393+5

Рисунок 5 – Потенциальная функция системы после конфликта
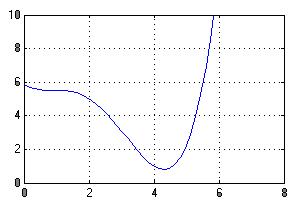
Рисунок 6 – Зависимость Е(х) (при х=4, E(4)=1%)
3.2 Динамическая модель технического противоречия
Считаем, что система градиентная:
![]()
![]()
![]()
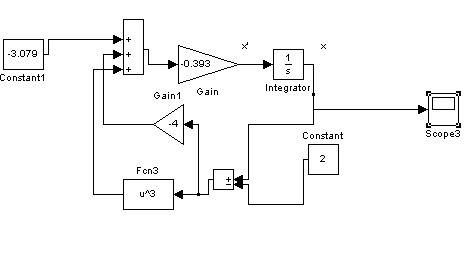
Рисунок 7 – Схема динамического моделирования технического противоречия
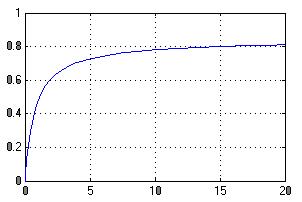
Рисунок 8 – График моделирования технического противоречия![]()
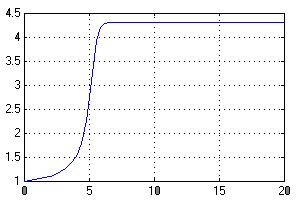
Рисунок 8 – График моделирования технического противоречия ![]()
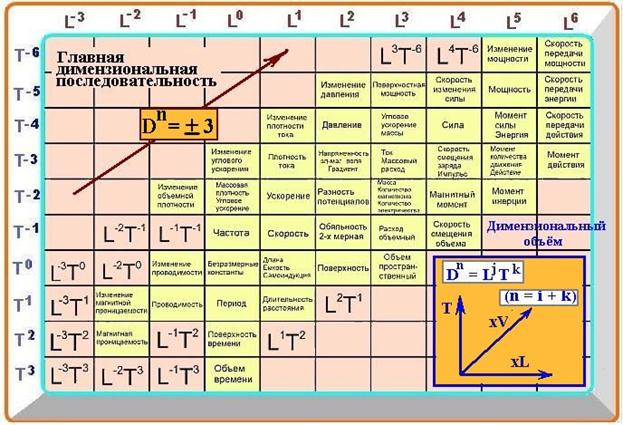
4. Решение поставленной задачи с использованием таблицы Бартини пространственно-временных величин
Таблица 1 – Система пространственно-временных величин
E(x)=(0,25 x4 – 0,5 d y x2 – e z x)f (4)
Для данной задачи выберем следующие размерности этих
величин:
· x=[ L0T-1]
· d=[ L0T-1]
· y=[ L0T-1]
· f=[ L0T4]
Если выбрать величину e=[ L0T-2] то размерность z=[ L0T-1], то есть Икс- элемент имеет значение частоты звука:
1) То есть возможное решение связано как-то с частотой звука – его высотой, а именно фильтрация звука определенной частоты, когда музыкант при импровизации делает ошибки и играет ноты из другой тональности. Необходимо использовать какой-либо частотный фильтр – это вполне возможно при импровизации на электроинструментах – электрогитаре, синтезаторе и т.д.
2) Возможное решение это не только фильтрация – удаление не нужных нот, но это и также постройка нот до частоты, которая соответствует тональности. То есть какое-то
устройство анализирующее мелодию, и когда ноты не попадают в тональность, оно их подстраивает – повышает или понижает на какое-либо количество полутонов или тонов.
Если выбирать также другие значения размерности коэффициента e, то zможет иметь размерность [ L0T0], [ L0T-1], [ L0T-2], [ L0T-3] и т.д. , возможны и другие варианты [ L0T1], [ L0T2], [ L0T3] и т.д., но все они будут связаны с временной
координатой, которая и есть решение нашей задачи.
Можно было бы попытаться выбрать eучитывая пространственную координату, но это не отразило бы специфику данной задачи и не привело бы к возможному решению.
5. Поиск решения проблемы cиспользованием генетических алгоритмов
Для моделирования системы мысленного поиска решения изобретательской задачи будем использовать дифференциальное уравнение Лотки-Вольтера для описания развития популяций вида:
![]() (5)
(5)
где х и у — конкурирующие свойства прототипа, z — новое свойство икс-элемента, к — коэффициент психологической инерции, а – коэффициент остроты мышления.
Когда решение найдено, то есть определено свойство икс-элемента, система находится в равновесном состоянии, которому соответствует
![]() . В этом случае уравнение (5) примет вид:
. В этом случае уравнение (5) примет вид:
![]() (6)
(6)
где ![]() - постоянная величина.
- постоянная величина.
5.1. Поиск решения изобретательской задачи на основании уравнения баланса ресурсов
Для составления уравнения баланса ресурсов будем анализировать только родительский тренд.
Определим родительский тренд:
Система имеет временное решение и соответственно передается ген времени, и он
представляет собой [L°Т1].
Тогда [с] = [L0Т1]
В качестве свойств х и у будем выбирать свойства изделия и инструмента соответственно. Можно составить формулу баланса ресурсов в виде:
[LnzТmz]= [LnxТmx] ·[LnyТmy] (7)
где nz, mz, пх, mх, пу, ту - соответствующие выбранным физическим свойствам степени по таблице 1.
На основании формулы (7) составим уравнения баланса ресурсов и определим свойства икс-элемента и соответствующее этому потенциальное решение изобретательской задачи
- свойство изделия – частота, свойство инструмента – частота
[LnzТmz]= [L°Т1][L0Т-1] ·[L0Т-1] nz=0, mz=-1
Для икс-элемента это будет соответствовать свойству частота.
Попробуем решить задачу иначе- используем те свойства которыми должен обладать икс-элемент- он во первых должен обладать хорошей частотой звука -высота звука [L0Т-1] а во вторых продолжительностью нот – должна соответствовать тактам, то есть [L0Т1] .
Тогда [с] = [L0Т-1] · [L0Т1] = [L°Т°]. Мы находимся нулевом тренде, но особенность нашей задачи такая, что она имеет решение только во временной области, то есть передается ген времени. И если поискать решение в области [L°Тn] меняя n, то мы опять приходим к решению z=[L0Т-1] - частота звука.
То есть разными подходами получено одно решение.
5.2. Оценка эффективности решений по ресурсозатратности
Для оценки затрат ресурсов решения будем использовать формулу:
R=√nz2 + mz2 (8)
где R можно определить как модуль использования вещественно-полевых ресурсов.
Наиболее эффективному решению здесь будет соответствовать минимум значения R . Это соответствует минимальному перемещению от клетки (L°,Т°) в таблице 1.
Можно провести аналогию с анализом вещественно-полевых ресурсов, когда лучшим решением будетпустота, то есть ничто.
Для приведенных решений эффективность R=1. А это и есть наиболее эффективное решение – мы сместились из (L°,Т°) на одну клетку.
6. Анализ смены представлений
Для данной задачи рассмотрим изменение смены представлений при движении по родительскому тренду. У нас при переходе от одной клетке к другой прибавляется ген времени. И в принципе каждая клетка должна наталкивать нас на решение. Время в
секундах- период. Период на частоту. Так физически связанны эти понятия.
Поэтому двигаясь в отрицательном направление – когда уменьшается степень Т. Мы видим все время L0T-n , где n- положительное целое число.
То есть можно представить как совокупность произведения множителей T-1 . Которые как раз являются решением данной задачи. То есть используем не один фильтр а два и т.д.
А когда движемся в положительном направлении – когда увеличивается степень Т. Мы видим все время L0Tn , где n - положительное целое число. Период T1 величина обратная частоте T-1 – но в нашем сознании легко происходят превращения восприятия одного в другое. И мы опять приходим к тому же решению. В нашем сознании происходит замена переменной – замена одного представления другим– так как человек
противоречив, он любит рассматривать крайние противоположные решения.
Противоречие – столкновение двух противоположных понятий, вот что есть прогресс. Борьба противоположностей. Поэтому мы легко можем получить решение как двигаясь в одном направлении, так и в другом. В нашем сознании все едино. И все может отображаться из одной крайности в другую.
И при этом конкретно для данной задачи– здесь каждая клетка есть решение – потому что переход от одной к другой есть совокупность умножения исходной L0Tnна
множитель L0T±1. То есть несколько сомножителей. Разбиение происходит как на
элементарные звенья передаточных функций.
Поэтому решение смены представлений при смещении на 1,2,3,4 и т.д. клетки даст один и тотже результат. Просто увеличится количество блоков для решения.
7. Анализ полученных результатов, их адекватность реальности. Применение на практике
Отметим особенность данной проблемы – она имеет только временное решение, в пространстве координата L=0. Это специфика данной задачи, что стоит искать решение только по временной координате базиса Бартини.
Решение вполне реально и может быть использовано при создании музыкальных электронных инструментов. Что позволит начинающим музыкантам импровизировать, совершая меньше ошибок.
Кстати, следует отметить, данное решение может также помочь музыкантам, когда они просто играют какое-либо произведение и делают ошибки, путают ноты и берут из другой тональности, это режет слух, а используя решение – повышение или понижение частоты звука – подстройка нот, позволит решить эту проблему.
В заключении хочется отметить раз импровизация (франц. improvisation, итал. improvvisazione, от лат. improvisus — неожиданный, внезапный) создание художественного произведения непосредственно в процессе его исполнения. То музыка есть процесс создания нового, с помощью нашего разума, представлений о гармонии и взаимосвязи в музыке, предыдущего опыта, ранее услышанных музыкальных произведений и творческого начала в каждом человеке.
И поэтому импровизации как проблема создания нового, есть задача изобретательская и к ней могут быть применены все изобретательские методы, возможно математическое описание музыки – так как вообще музыка сродни математике, в ней есть определенный порядок – гармония, деления на такты, длительность нот определенная и многое другое…
Но это уже проблема для решения в будущем…
Библиографический список
- Арнольд В.И. «Теория катастроф» М.: Наука, 1990.
- Алексеев Ю.К. «Введение в теорию катастроф» М.: МГУ, 2000
- А.П.Кузнецов Колебания, катастрофы, бифуркации, хаос. – Издательство ГосУНЦ «Колледж», Саратов 2000. – 87 с.
- Ди Бартини Р.О. Некоторые соотношения между физическими константами. Доклады Академи и наук СССР 1965. Том 163, N. 4. C.861-864.
- Ди Бартини Р.О., Кузнецов П.Г. Множественность геометрий и множественность физик. // Материалы семинара “Кибернетика электроэнергетических систем”. Брянск,1974.
- Бушуев А.Б. Моделирование противоречий в АРИЗ. “Metodolog.ru” , 2005
- Бушуев А.Б. Математика, ТРИЗ, Бартини и кое-что еще. “Metodolog.ru” , 2005
- http://ru.wikipedia.org/wiki/Импровизация
Количество просмотров публикации: Please wait


