Введение

Достижения современной электроники поистине фантастичны. Я помню времена, когда оборудование, необходимое для хранения информации, помещающейся теперь в одной «флэшке», занимало несколько шкафов. Все эти достижения связаны с использованием удивительных свойств магнитного поля. Но что представляет собой магнитное поле? Вследствие чего возникает и куда исчезает? До сих пор наука не даёт определённого ответа на эти тривиальные вопросы. В учебнике, выпущенном в 1964 г. мы находим, что вокруг проводника с током возникает магнитное поле и магнитное поле является носителем ряда физических свойств [1, с. 182]. Учёбник, выпущенный в 2006 г. лишь констатирует, что взаимодействие токов осуществляется через поле, называемое магнитным [2, с. 116].

Одним свойств магнитного поля является наличие так называемых «силовых линий». Экспериментально эти силовые линии детектируются с помощью железных опилок (см. рис. 1).

Но магнитное поле создаётся не только проводниками с током, но и специфическими веществами – магнетиками, которые приобретают это свойство под действием внешнего магнитного поля. Согласно классической теории принцип намагничивания заключается в том, что во всех веществах существуют мельчайшие электрические токи, замыкающиеся в пределах каждого атома (молекулярные токи). Если магнетик не намагничен, то он не создаёт магнитного поля. Это значит, что молекулярные токи в нём расположены беспорядочно, так что суммарное их действие равно нулю. При намагничивании магнетика расположение молекулярных токов становится частично или полностью упорядоченным [1, с. 240].

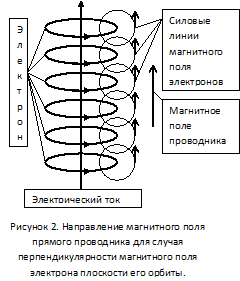
Представления о молекулярных токах были введены в теорию магнетизма ёще Ампером [3]. Ныне они имеют базу в виде модели атома по Бору-Резерфорду, в которой электрон движется вокруг ядра по круговой орбите [4]. Это движение может создавать электрический ток, так что электронную орбиту можно рассматривать как круговой проводник или виток соленоида. Собственно, на этой основе вводится понятие магнитного момента электрона [1, с. 273]. Тогда электрический ток в проводнике можно представить как последовательность подобных электронных колец (см. рис. 2).

Но если магнитное поле проводника представить как суперпозицию магнитных полей электронов, оно будет аналогично магнитному полю соленоида и направлено вдоль проводника, что противоречит эксперименту.

1. Магнитное поле электрона

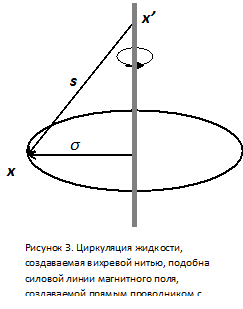Соответствие опытным данным требует, чтобы силовые линии магнитного поля электрона были коаксиальны его орбите. Специалисты в области гидромеханики давно отметили аналогию между уравнением для нахождения скорости циркуляции, создаваемой вихревой нитью, и уравнением Био-Савара для магнитного поля, создаваемого вокруг замкнутого проводника с постоянным током [5, c. 130]. Действительно, скорость циркуляции, создаваемой бесконечной вихревой нитью на расстоянии σ определяется уравнением (см. рис. 3):

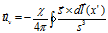
             ,             (1)

где χ – интенсивность вращения вихревой нити.

Аналогично, напряжённость магнитного поля, создаваемого бесконечным проводником с током, определяется уравнением [1, с. 183]:

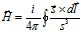, (2)

где: i – сила тока.

На аналогию между силовыми линиями магнитного поля и линиями тока гидродинамических течений указывал и Пуанкаре [6, с. 46].

Это согласуется с представлениями о вихревом характере магнитного поля и электрического поля, создаваемого электромагнитным излучением. В работах классиков теории электромагнетизма – Фарадея и Максвелла – использовалось представление о том, что пространство заполнено некой субстанцией – эфиром. В.А. Ацюковский использовал для описания ядерных взаимодействий модель газовых торроидальных вихрей [7]. Но газоподобная среда, так же как и среда со свойствами жидкости не обладает жёсткостью, необходимой для фиксации силовых линий в пространстве. И.П. Верменчук считал [8], что все взаимодействия: и гравитационные, и электрические, и магнитные можно описать через взаимодействия вихрей в сплошной среде – эфире. Причиной образования вихрей является движение материальных тел. А.М. Куминым в качестве структурных элементов эфира были предложены «вращающиеся материальные объекты», подобные шарикам [9].

В данном случае мы ограничимся только образованием магнитного поля. Итак, движущийся электрон, который представляет собой стоячую волну, распределённую по окружности орбиты, подобно диску, вращающемуся в жидкости, создаёт вокруг себя циркуляцию эфира. Тогда линии тока эфира будут совпадать по направлению с силовыми линиями магнитного поля проводника.

Чтобы уточнить характер этих циркуляций, рассмотрим ещё два эффекта.

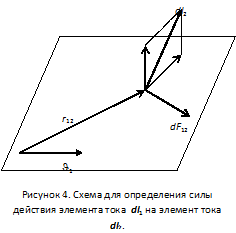
Сила dF₁₂, с которой элемент проводника dl₁ действует на элемент проводника dl₂, направлена перпендикулярно к последнему и лежит в плоскости, содержащей dl₁ и r₁₂
(см. рис. 4). При этом направление силы dF₁₂ подчиняется правилу правого буравчика: т.е. направлению движения винта с правой нарезкой при вращении его головки от элемента dl₂ к нормали dl_2n. Направление нормали также определяется правилом правого буравчика: т.е. совпадает с направлением движения винта с правой нарезкой при вращении его головки от dl₁ к r₁₂. Модуль силы dF₁₂
определяется уравнением
[1, с. 175]:

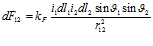,     (3)

где: i₁ и i₂ – сила тока в элементах проводников; J₁ – угол между dl₁ и r₁₂, J₂ – угол между dl₂ и нормалью к плоскости, содержащей dl₁ и r₁₂.

Во-первых, необходимо обратить внимание на то, что сила магнитного взаимодействия направлена под углом к радиус-вектору, соединяющему проводники. Т.е. она стремится не притянуть или оттолкнуть, а повернуть проводники таким образом, что бы величина силы стала равной нулю. Во-вторых, если расположить проводники на одной линии, то sinJ₁ будет равен нулю, а, следовательно, будет равна нулю и сила магнитного взаимодействия. Если представить, что электроны это и есть элементы тока, то это означает, что они создают циркуляцию только в плоскости орбиты. В этом есть глубокий философский смысл. В противном случае электрон замыкал бы своим магнитным полем на себя всю Вселенную. Можно считать, что толщина орбиты электрона и циркуляции эфира, им создаваемая, величины бесконечно малые. Магнитные взаимодействия между электронами заставляют их выстраиваться в параллельных плоскостях, что создаёт условия для формирования электронных структур атомов и молекул.

Традиционно принято считать направлением электрического тока, направление, противоположное движению электронов [1, с. 124]. Тогда для электронов будет действовать правило левого буравчика: направление движения электрона по орбите и направление движения создаваемых электроном циркуляций эфира совпадает с движением головки винта с левой нарезкой при его поступательном движении вперёд.

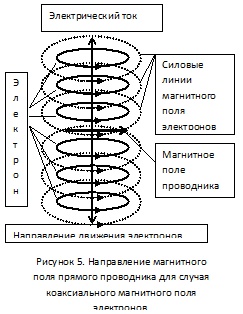
С учётом всего вышесказанного рис. 2 преобразуется в рис. 5 и мы получаем качественное соответствие между суммарным магнитными полем электронов и магнитным полем проводника.

2. Напряжённость магнитного поля электрона.

Величина напряжённости магнитного поля элемента проводника выводится из уравнения для силы магнитного взаимодействия между элементами тока, подобно тому, как вводится величина напряжённости электростатического поля для электростатического взаимодействия. В системе СГСМ величина напряжённости поля элемента тока равна [1, с. 183]:

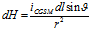,                                     (4)

где: J – угол между направлением тока и радиус-вектором пробной точки.

Такое определение напряжённости магнитного поля, однако, неудобно для рассмотрения свойств электрона. Мы уже установили, что магнитное поле электрона существует только в плоскости орбиты, поэтому исключим угол J. Поскольку речь пойдёт о единичном электроне, мы исключим элемент длины и введём новую величину – напряжённость циркуляции – H_C. Сила тока в единицах СГСМ получается делением силы тока в системе СГСЭ на скорость света. Если принять, что dq = e (заряду электрона), то dt – это время между двумя последовательными электронами, а 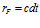– расстояние, на которое за это время распространится циркуляция от предыдущего электрона. Чем больше r_F, тем меньше будет остаточная циркуляция в пробной точке:

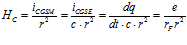.                             (5)

Для неподвижного электрона, т.е. для электрона, положение которого в пространстве зафиксировано, например, в постоянном магните, член 1/r_F исключается. Таким образом, напряжённость магнитного поля электрона оказывается формально равной напряжённости его электростатического поля:

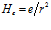.                                         (6)

Но магнитное поле действует только в плоскости орбиты электрона и направлено тангенциально к линиям тока эфира, коаксиальным орбите электрона.

3. Взаимодействие магнитных полей электронов

Что бы перейти от гипотезы к теории необходимо смоделировать процессы взаимодействия между собой магнитных полей электронов в различных условиях и оценить связанные с этим эффекты. Здесь перед нами открывается широкое поле для творчества.

Влияние вещества проводника на напряжённость магнитного поля. Уравнение (4) справедливо для нахождения напряжённости магнитного поля в вакууме. Если пространство вокруг проводника заполнено каким-либо веществом, то магнитное поле будет отличаться от магнитного поля в вакууме, пропорционально некоторой величине, называемой магнитной проницаемостью вещества. Но данные о влиянии на напряжённость магнитного поля состава проводника отсутствуют. Это свидетельствует о том, что, по крайней мере, в первом приближении, напряжённость магнитного поля не зависит от свойств вещества проводника, а зависит только от силы тока в проводнике. В то же время мы знаем, что радиусы орбит электронов в различных металлах существенного различаются. Следовательно, должны существенно различаться и существующие в них «молекулярные токи».

Это свойство магнитного поля вполне объяснимо с позиций циркуляционной модели. Дело в том, циркуляция, определяемая как произведение радиуса на круговую скорость, есть величина постоянная [10, с. 47]:

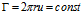, где u – круговая скорость линии тока.                     (7)

Величину константы мы можем найти из величины момента количества движения электрона, который равен [4]:

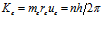, где h – постоянная Планка.                  (8)

Отсюда следует:

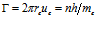.                                      (9)

В работе [11] было показано, что в модели бора n=1 для всех электронов в основном состоянии, независимо от номера так называемого «электронного слоя». В теории строения атома принято, что электроны располагаются вокруг ядра так называемыми «слоями» [12, с. 93]. На электрон верхнего слоя действует эффективный заряд, складывающийся из заряда ядра и экранирующих заряд электронов. Вычисляя радиус орбиты внешнего электрона в основном состоянии по модели Бора мы для любого слоя, будь то 2s или 5s, должны принимать n=1, потому что значения n>1 соответствуют возбуждённым состояниям электрона, в которые он переходит под воздействием внешнего излучения. И время нахождения электрона в возбуждённом состоянии ничтожно мало.

Таким образом, скорость циркуляции, с которой может быть связана напряжённость магнитного поля, не зависит от радиуса орбиты электрона, а зависит лишь от расстояния между ядром атома и пробной точкой.

Тепловое излучение. Целесообразно выделить особый вид движения электронов – вращение плоскостей орбит вокруг ядра. В этом случае в окружающем пространстве будет всё время меняться магнитное поле, причём с определённой частотой – с частотой вращения плоскостей орбит. Представляется, что подобное вращение является одним из основных видом теплового движения, с которым связана теплоёмкость и теплопроводность.

Вращение плоскости орбиты электрона связано с изменением момента количества его движения. Производимая при этом работа определяется соотношением:

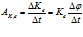,                                      (10)

где ΔК_e – изменение момента количества движения электрона, а Δφ – угол поворота плоскости орбиты.

Закон сохранения энергии требует, что бы эквивалентное количество энергии выделилось в окружающую среду. Мы можем предположить, что это будет энергия циркуляции эфира.

Величина момента количества движения электрона равна h/2π. Следовательно, при повороте плоскости орбиты на 360 градусов величина работы будет равна:

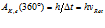,                                     (11)

где ν_Rot – частота вращения плоскости орбиты.

Взаимодействие циркуляций. Каким образом, циркуляции, создаваемые отдельными электронами взаимодействуют между собой?
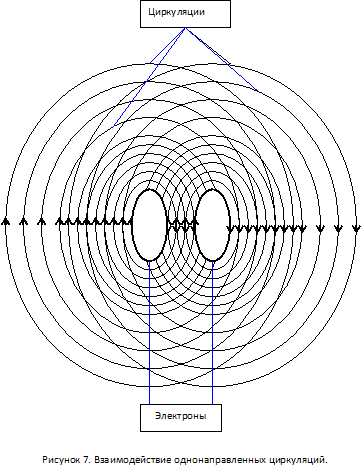
Это важнейший вопрос, от ответа на который зависит, станет ли рассматриваемая гипотеза теорией или нет. Качественная оценка показывает (см. рис. 6), что однонаправленные циркуляции взаимно уничтожаются во внутренней области и должны усиливать друг друга во внешней области. Циркуляции, имеющие противоположное направление, будут взаимно усиливаться во внутренней области и отталкиваться во внешней. Но является ли это взаимодействие аддитивным или имеет место более сложная зависимость?

Нам еще предстоит дать ответ на это и многие другие вопросы, связанные с использованием циркуляционной модели для описания явлений магнетизма.

Библиографический список

1. Калашников С.Г. Электричество: учебное пособие. – М: Наука, ГРФМЛ, 1964. – 666 с.
2. Савельев И.В. Курс общей физики: учебное пособие в 3-х томах, т. 2. – СПб.: Лань, 2006. – 496 с.
3. Ампер А.-М. Электродинамика./Ред. Я.Г. Дорфман. – М.: Изд-во АН СССР, 1054, с. 271.
4. Бор Н. Избранные научные труды. Т. 1. – М.: Наука, 1970, с. 84-148.
5. Бэтчелор Дж. Введение в динамику жидкости./пер. с англ. – М.: Мир, 1973.
6. Пуанкаре А. Теория вихрей. – Ижевск: НИЦ «Регулярная и хаотическая механика», 2000. – 160 с.
7. Ацюковский В.А. Общая эфиродинамика. Моделирование структур вещества и полей на основе представлений о газоподобном эфире. – М.: Энергоатомиздат, 1990. – 280 с.
8. Верменчук И.П. Эфирно-вихревая модель микромира. // Русская Мысль, 1993, № 1-2, с. 63-72.
9. Кумин А.М. Механизм проточно-столкновительного взаимодействия.//Интернет-сайт SciTecLibrary.ru, 22.04.2003. URL:http://sciteclibrary.ru/rus/catalog/pages/5077.html.
10. Карман. Т. фон. Аэродинамика: избранные темы в их историческом развитии./пер. с англ. – Ижевск: НИЦ «Регулярная и хаотическая динамика», 2001. – 208 с.
11. Островский Н.В. Алгоритм вычисления квантованного радиуса орбиты электрона. //Интернет-конференция “Информационно-вычислительные технологии в науке”. Дата публикации 23 декабря 2009 г. URL: http://www.ivtn.ru/2009/pdf/d09_18.pdf.
12. Дей К., Селбин Д. Теоретическая неорганическая химия. – М.: Мир, 1971. – 416 с.

Все статьи автора «onv1»