АППРОКСИМАЦИЯ НЕЧЕТКОГО МНОЖЕСТВА, ПОЛУЧЕННОГО В РЕЗУЛЬТАТЕ ОПЕРАЦИИ НЕЧЕТКОГО ВЫВОДА, НЕЧЕТКИМ ЧИСЛОМ

В результате осуществления операций над нечеткими числами, например в ходе операции нечеткого вывода в общем случае мы получаем нечеткое множество 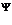, не отвечающее требованиям, предъявляемым к нечетким числам:

1) Нечеткое число должно иметь хотя бы один элемент, 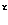 для которого выполняется следующее условие [3]:

2) Нечеткое число должно удовлетворять условиям выпуклости:

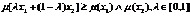
Так как результатом нечеткого вывода является нечеткое множество 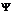дальнейшее использование данного множества в вычислениях невозможно, поскольку операции, применяемые к нечетким числам и нечетким множествам различны.

А именно операция произведения нечетких чисел и тех же чисел представленных нечеткими множествами, различаются, вследствие того, что операция нечеткого расширения не рассматривает множества, как числа, в результате так же получается нечеткое множество, не отвечающее требованиям п. 1 и п. 2.

          Поэтому над нечетким множеством 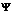выполняется операция дефаззификации.

Наиболее распространенной и корректной, в плане получаемого результата, является использование метода «центра тяжести», позволяющего учитывать все «подмножества» исходного множества 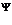. Результатом этого оператора на выходе получается число 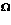, а не множество [3]:

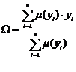
То есть в результате применения оператора деффаззификации происходит потеря информации.

Особенно эффект потери информации важно учитывать в том случае когда над множеством 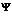требуется выполнить еще ряд операций.

Предлагаемый подход позволит использовать нечеткое множество, 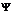для дальнейших преобразований предварительно преобразовав его в нечеткое множество 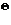, удовлетворяющее  условиям (1) и (2) и в то же время, имеющего достоинства метода «центра тяжести» и минимизирущего потерю информации.

Положим 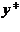 результат деффаззификации методом «центра тяжести», а 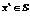где 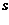множество элементов множества 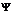. Тогда значение .

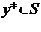Поскольку множество 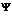в общем случае дискретно, то значение  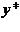принадлежит некоторому интервалу множества 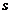, а именно .

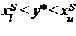При этом существует три граничных случая:

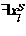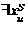1) Если и то ;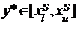

2) Если отношение 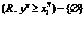 то, 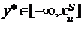 т.е. когда 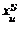является граничным значением, поэтому в качестве центра нечеткого числа 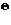выбирается ;

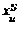3) Если отношение 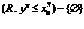, то 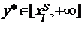 и центром нечеткого числа 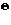выбирается .

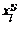Первый случай отличается от второго и третьего случаев тем, что в качестве кандидата на центр числа является как число 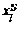так и 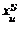. В данном случае выбор производится по правилу максимума функции принадлежности:

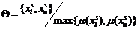
Если 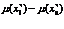 то выбирается любое из них.

Так же стоит отметить, что можно использовать интерполяцию для получения значения .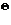

Таким образом, используя метод «центра тяжести» мы получаем наиболее вероятное положение центра числа .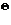

Для подготовки множества к нормализации выполним следующую операцию:

Для всех 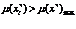положить.

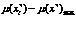Далее производим операцию аппроксимации множества, учитывая ограничения выпуклости.

Для этого выделим ключевые точки и получим результирующее множество.

Полученное множество удовлетворяет условиям выпуклости, поэтому для получения из этого множества  нечеткое число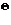остается лишь нормализовать его. Для нормализации используется соотношение [4]:

Алгоритм аппроксимации множества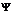

Для начала необходимо определить краевые точки нечеткого множества 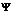 они будут служить начальным приближением нечеткого числа.  Для этого выделим точки множества  , ,
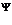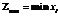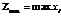
и .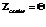

Постановка задачи: для нечеткого множества 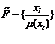 подобрать такие значения вектора  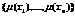при ограничениях ,,
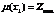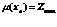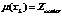
и векторе 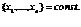, чтобы величина .

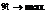Величина 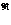 может быть определена как [2]:

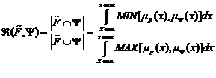
Для дискретных множеств:

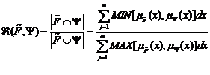
где 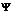- исходное нечеткое множество, полученное после процедуры нечеткого вывода, а 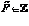, где 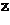- это множество всевозможных выпуклых нечетких множеств подходящих для аппроксимации множества .

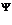          Для поиска «оптимального» нечеткого множества 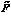 использовался генетический алгоритм (ГА) [1].

Размер хромосомы N, N – это количество точек по которым будет аппроксимироваться множество.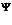

Хромосомы состоят из чисел в диапазоне от 0 до 1, т.е. по своей сути являются функцией принадлежности множества .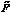

В качестве операции мутации была выбрана стандартная операция: случайным образом выбирается элемент хромосомы и изменяется, вероятность мутации 0,1.

Для скрещивания использовался стандартных алгоритм: родители обмениваются частями своих хромосом в случайно выбранном месте, вероятность скрещивания была задана 0,7 .

Стоит отметить, что в операциях скрещивания и мутации необходимо отслеживать значения ,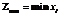
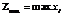
и .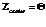

В качестве функции соответствия используется выражение для .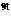

В общем случае выделенные точки поверхности, в результате работы проведенной ГА, могут и не образовывать выпуклое множество.

Для удовлетворения условию п.2, по точкам поверхности необходимо строить выпуклую оболочку по алгоритму Джарвиса [5]:

1)     Ищем левую крайнюю точку 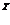, если таковых несколько, то используем ту, которая находится ниже;

2)     Используя 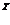как начальную точку, образуем векторы с двумя точками нечеткого множества 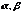, вычисляя координаты векторов как:

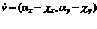
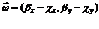
3)     Определяем взаимное положение векторов 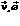относительно друг друга. Для этого найдем векторное произведение векторов.

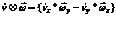
4)     Если полученная величина больше нуля то вектор , т.е. находится слева от .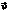

5)     Если полученная величина меньше нуля то вектор 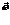, находится справа от .

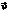6)     Если полученная величина равна нулю то вектор 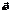, параллелен вектору  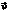и для определения оптимального вектора, выбирается тот, который находится ближе.

В результате для каждой хромосомы может быть вычислена величина .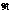

По результатам работы ГА выбирается хромосома, для которой величина 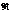 достигает максимального значения.

Из рисунка 5 видно, что в результате применения приведенного алгоритма поверхность нечеткого множества аппроксимируется нечетким числом.

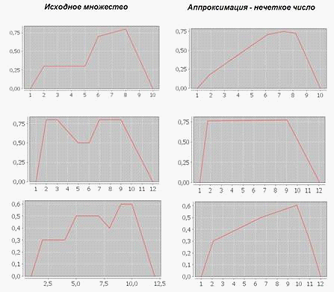
Рисунок 5 – Результаты применения предложенного алгоритма

Библиографический список

1. Haupt, R., Haupt, E. (2004). Practical genetic algorithms (Second edition). New Jersey: John Wiley & Sons, Inc.
2. Babuska, R. (1999). Fuzzy Modeling for Control. Boston: Kluwer Academic Publishers.
3. Piegat, A. (2009). Fuzzy modeling and control. New York: Physica-Verlag.
4. Hanss, M. (2005). Applied Fuzzy Arithmetic: An Introduction with Engineering Applications. New York: Springer Berlin Heidelberg.
5. Avis, D., Bremner, D., Seidel, R. (1997). How good are convex hull algorithms. Computational Geometry: Theory and Applications, vol. 7, pp. 265–301.

---

Количество просмотров публикации: Please wait

Все статьи автора «megoplay20»