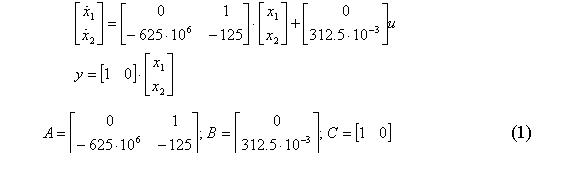Введение. Задача создания высокоточных и миниатюрных исполнительных устройств линейных микроперемещений в настоящее время имеет большое практическое значение. В полной мере она может быть решена при использовании современных пьезоэлектрических исполнительных устройств, построенных на основемногослойных пьезоактюаторов. По сравнению с пакетными устройствами предыдущего поколения они имеют меньшие габариты и обеспечивают большие значения перемещений при на порядок пониженном напряжении управления. Применение данных актюаторов, в качестве активных элементов пьезоэлектрических приводов, позволяет решать многие задачи в различных областях науки и техники. Колебательный характер переходных процессов имеет место улюбых пьезоэлектрических исполнительных устройств и многослойные актюаторы не являются исключением. При построении прецизионных систем позиционирования наличие таких колебаний затягивает переходные процессы и снижает точностные характеристики.
1. Статья подготовлена при финансовой поддержке РФФИ (Грант 08-09-00857-а)
2. Статья подготовлена при финансовой поддержке Конкурса грантов для студентов, аспирантов вузов и академических институтов, расположенных на территории Санкт-Петербурга
В данной работе рассматривается алгоритм управления пьезодвигателем, обеспечивающий апериодический характер переходного процесса и полную компенсацию колебаний.
На рисунке 1 представлена схема моделирования пьезодвигателя, который представляет собой пьезокерамический стержень со следующими параметрами:
Таблица 1 – Параметры пьезодвигателя
|
Длина |
 |
| Площадь поперечного сечения |  |
| Коэффициент усиления |  |
| Внутреннее сопротивление |  |
| Емкость пьезоэлемента |  |
| Пьезомодуль |  |
| Модуль Юнга |  |
| Коэффициент упругости |  |
| Коэффициенты прямогои обратного пьезоэффекта |  |
| Масса пьезоэлемента |  |
| Масса стола |  |
| Суммарная масса |  |
На рисунке 2 – переходной процесс. При подаче постоянного напряжения равного 10В на вход системы, перемещение на выходе составит 0.7 мкм. Переходный процесс – апериодический с наложеннымина него затухающими колебаниямис максимальной амплитудой составляющей 8% от установившегося значения.
Упрощенная модель пьезодвигателя. Если пренебречь внутренней обратной связью по скорости ( 
), влиянием жесткости конструкции, так как ее влияние мало по сравнению с упругостью( 
) Тогда можно представить модель пьезопривода в виде 2 звеньев – колебательного и апериодического, последнее соответствует высоковольтному усилителю на входе, модель представлена на рисунке 3.
Для синтеза алгоритма управления перейдем к описанию привода с учетом его характеристик в пространстве состояний:
Проверим пару А,С на полную наблюдаемость
Определитель 
не равен нулю, то есть система полностью наблюдаема. Ее переходной процесс на рисунке 4.
Разработка алгоритма управления.
Допустим мы хотим нулевое перерегулирование и время переходного процесса менее 1секунды.
Расчет: нулевое перерегулирование системе 2 порядка может обеспечить только полином Ньютона :
(3)
Время переходного процесса связано с корнями
соотношением : 
;или чтотоже самое
; (4)
Для проектируемой системы выберем
, тогда ХП примет вид : 
Построим эталонную модель 
где
соответственно векторы состояния и выхода 
,
соответственно матрицы состояния и выхода.
Алгебраическим спектром собственных значений
матрицы
является 
=
=–48, сообщение которого матрице состояния
проектируемой системы может доставить последней желаемые динамические свойства
в переходном и установившемся режимах. Совпадающие собственные значения матриц Ги 
отсутствуют, то есть выполняется условие
;
Матрица примет вид :
=
(5)
Выберем матрицу
из условия полной наблюдаемости матриц 
=
(6)
Матрица
векторного преобразования подобия удовлетворяет матричному уравнению Сильвестра :
(7)
=
(8)
= 
(9)
Вычислим матрицу
прямой связи по экзогенному задающему воздействию 
из условия равенства выхода входу
в неподвижном положении 
, таким образом имеет представление:
=1000 (10)
На рисунке 5 – схема управления с Kxи Kgрегулятором. На рисунке 6 – переходной процесс.
Вывод: таким образом, в результате моделирования установлено, что разработанный регулятор для управления пьезоэлектрическим исполнительным устройством на базе многослойной тонкопленочной пьезокерамики, обеспечивает полную компенсацию колебаний в переходном процессе, при его апериодическом характере и заданном времени переходного процесса. Использование такого алгоритма управления пьезоэлектрическим исполнительным устройством в системах позиционирования позволит повысить их точностные характеристики.
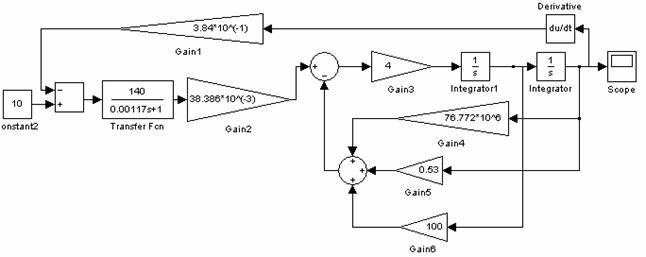
Рис. 1 – Математическая модель пьезодвигателя
Рис. 2 – График переходного процесса для модели, представленной на рисунке 1
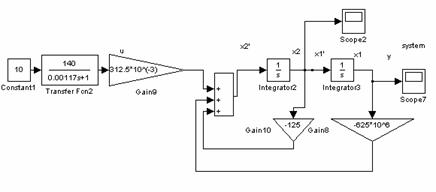
Рис. 3 –Упрощенная математическая модель пьезодвигателя в пространстве состояний
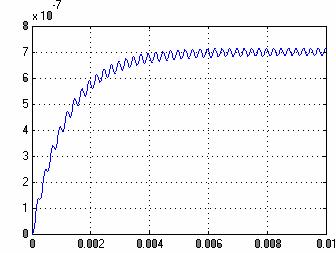
Рис. 4– График переходного процесса для модели, представленой на рисунке 3
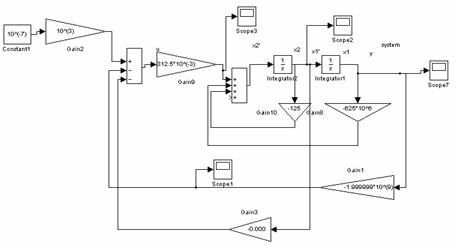
Рис. 5– Схема управления пьезоприводом с Кх и Кg регулятором
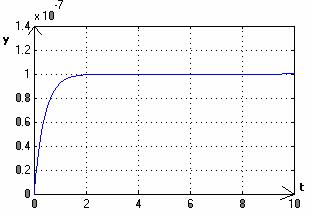
Рисунок 6– Переходной процесс в системе, представленной на рисунке 5
Библиографический список
- Бобцов А.А., Бойков В.И., Быстров С.В., Григорьев В.В., Коровьяков А.Н. Комплекс для исследования адаптивного управления пьезоприводом. – Сб. Материалы 1-й Российской мультиконференции по проблемам управления. Мехатроника, автоматизация, управление.- 2006, с.308-313.
- Бобцов А.А., Бойков В.И., Быстров С.В.,Григорьев В.В. Разработка и исследование пьезопривода на основе многослойных тонкопленочных пьезоактюаторов. 2-я Российская мультиконференция по проблемам управления. Доклады 5-я Научная конференция «Управление и информационные технологии» (УИТ-2008), т.2, СПб.- 2008, с.172-176.
- Никольский А.А. Точные двухканальные следящие электроприводы с пьезокомпенсаторами.- М.: Энергоатомиздат, 1988.- 160 с.
- В.И.Бойков, С.В. Быстров , В.В. Григорьев, Д.Е. Обертов. Пьезопривод на основе тонкопленочных пьезоактюаторов / Приборостроение СПбГУ ИТМО. Том 11. Авионика и управление в технических и информационных системах. СПб: СПбГУ ИТМО, 2009. 98 с